|
Modele stochastice de prognoza
1 Functia de autocorelatie
Evolutia fenomenelor economice se afla sub impulsul resurselor existente, capacitatilor create, experientei acumulate, traditiei, ca si a altor factori de natura exogena. Astfel, o activitate productiva realizata la un anumit nivel si-a creat implicit o baza (capacitati de productie, resurse de munca, tehnologie) pentru a atinge si in perioada urmatoare cel putin acelasi nivel: investitiile implica, cel putin pana la finalizarea proiectului, noi investitii, consumul creeaza obisnuinta si deci genereaza consum etc. Ca urmare, multe dintre procesele economice depind de anterioarele lor performante, avand un caracter inertial care, in limbajul econometriei, este pus in evidenta prin autocorelatie.
In ceea ce priveste factorii exogeni, o schimbare brusca si de amploare intervenita in randul acestora se repercuteaza, de cele mai multe ori, in mod treptat asupra variabilelor - efect corelate direct, dar mai ales indirect, cu respectivul factor. Astfel, o crestere brusca a ofertei unui produs pe piata influenteaza nivelul pretului in sensul ca acesta va inregistra scaderi treptate in decursul timpului; aparitia unei noi tehnologii genereaza efecte discontinue, in trepte, asupra productiei si costului etc.
Luand in considerare astfel de particularitati ale comportamentului economic, pe de o parte, precum si posibilitatile de cuantificare si prognozare ale modelelor lag si ale modelelor autoadaptive, pe de alta parte, econometricienii americani George E. P. Box si K. G. M. Jenkins au elaborat, spre sfarsitul deceniului '60 asa numitele modele stochastice de prognoza. Intr-o formulare generala, un astfel de model se prezinta astfel:
![]() (1.1)
(1.1)
unde:
yt = variabila economica stationarizata, trendul fiind exclus din date;
a, b = parametri.
Observam ca prima parte a modelului (1.1) reprezinta un model liniar autoregresiv; iar cea de-a doua parte include eroarea introdusa prin intermediul valorilor variabilei reziduale (ut-j) in vederea corectarii prognozelor.
Urmatoarele considerente de natura economica si statistica au stat la baza elaborarii unor astfel de modele:
- procesul economic descris de seria cronologica este rezultatul actiunii mecanismelor interne - ceea ce explica natura autoregresiva a modelului - precum si a unor influente din afara, care, daca excludem tendinta generala si factorii care o determina, actioneaza accidental sub forma unor impulsuri aleatoare. Aceasta din urma caracteristica a procesului confera modelului un caracter stochastic;
- seria cronologica, reprezentand "materia prima" pentru modelare, se incadreaza intr-una dintre categoriile:
serie nestationara, avand tendinta evolutiva (rezultat al unui proces omogen nestationar);
serie stationara (rezultat al unui proces stochastic stationar), avand unele elemente stabile, repetabile ca desfasurare si care, retinute de model, confera prognozei o baza solida si implica sansa de a fi performanta;
serie pur aleatoare, rezultat al unui proces generator de numere intamplatoare;
- o clasa de procese stochastice, considerate utile in vederea analizei si prognozei seriilor cronologice, o formeaza procesele stochastice stationare. Comportamentul unor astfel de procese poate fi caracterizat prin functia de autocorelatie. In ceea ce priveste componenta reziduala, ut, aceasta este presupusa ca fiind generata de un proces de zgomot alb[1], in care fiecare termen urmeaza o distributie normala, de medie egala cu zero si de dispersie diferita de zero, avand, pentru k ¹ 0, covariante egale cu zero[2]. Mediile ponderate ale unor astfel de termeni pierd caracteristicile unui astfel de proces (de zgomot alb) constituind reprezentari satisfacatoare ale unui proces aleator obisnuit
- modelul este definit ca un agregat ce include impulsurile receptate cu intarzieri de 1, 2, . , p intervale de timp, ca si reactiile, exprimate in medie, la abaterile accidentale (ut) de la evolutia liniara , manifestate in urma cu 1, 2, . , q intervale de timp.
Aceste considerente isi gasesc corespondente reale in economie intrucat caracterul autocorelat al proceselor economice este recunoscut, iar in ce priveste introducerea in calcule a efectelor perturbatiei, aceasta se justifica daca avem in vedere fie si numai reactiile reparatorii (de redresare) pe care le genereaza abaterile de la ceea ce in economie se considera o evolutie normala.
Din punct de vedere al tehnicilor de masurare, considerentele mentionate presupun ca seria cronologica pe care urmeaza sa o prelucram in sensul metodei Box-Jenkins sa fie o verificare prin prisma urmatoarelor conditii:
- existenta unui numar suficient de mare de termeni (n > 40) astfel incat coeficientii statistici de autocorelatie precum si parametrii sa prezinte stabilitate;
- seria valorilor sa fie stationara (fara trend), incluzand eventual componente oscilatorii (sezonalitate, ciclicitate);
- FUNCTIA DE AUTOCORELATIE, care reprezinta elementul cheie pentru intreg demersul presupus de modelele stochastice de prognoza, poate fi estimata de coeficientul de autocorelatie, rk, definit astfel:
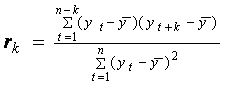 (1.2)
(1.2)
unde:
rk estimatorul coeficientului de autocorelatie[3];
k = intarzierea (lagul), exprimata printr-un numar de unitati dupa care apare efectul unor impulsuri (modificare a propriului comportament sau a unei cauze).
Exemplu
Fie urmatoarea serie de date trimestriale pentru trei ani succesivi privind o variabila economica:
Tabelul 1.1
|
|
I |
II |
III |
IV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Evident, numarul de termeni este mult prea mic, dar facem abstractie de aceasta prima conditie intrucat urmarim sa facilitam intelegerea etapelor de calcul suficient de laborioase pentru a nu mai incarca expunerea cu calcule prelungite.
Daca ne referim la celelalte conditii, atunci calculul coeficientilor de autocorelatie pentru k = 1, 2, 3, ., precum si testarea semnificatiei acestora ofera raspunsuri utile in vederea caracterizarii seriei.
Pentru datele exemplului considerat (tabelul 1.1) obtinem urmatorii coeficienti de autocorelatie:
![]()
![]()
![]()
![]()
Tendinta
de crestere evidenta a valorilor seriei, aspect confirmat de descresterea
relativ lenta a coeficientilor ![]() , semnaleaza o serie cronologica nestationara.
, semnaleaza o serie cronologica nestationara.
Pentru eliminarea acestui inconvenient procedam la calculul diferentelor de ordinul intai: 5-2 = 3; 6-5 = 1; . ; 22-20 = 2. Seria de valori astfel rezultata este prezentata in tabelul urmator:
Tabelul 1.2
|
Trimestrul (t) |
II |
III |
IV |
I |
II |
III |
IV |
I |
II |
III |
|
Valori stationarizate (ys) |
|
|
|
|
|
|
|
|
|
|
Coeficientii
de autocorelatie obtinuti pentru noile valori ale lui ![]() prezentate in tabelul 1.2
sunt:
prezentate in tabelul 1.2
sunt: ![]()
Descresterea
rapida a coeficientilor spre nivele apropiate de zero confirma stationaritatea
seriei. Mentionam ca ne-am limitat la coeficientii ![]()
![]()
![]() intrucat seria este
mult prea scurta. De regula, se determina
intrucat seria este
mult prea scurta. De regula, se determina ![]() pentru k = 1, 2, ., 6.
pentru k = 1, 2, ., 6.
In raport cu sursa care "alimenteaza" previziunea deosebim:
- modele autoregresive (AR):
de ordinul intai, AR(1), ![]()
de ordinul doi, AR(2), ![]()
in raport cu distanta in timp a valorilor trecute ale variabilei care determina viitorul nivel;
- modele de medie mobila[4] (MA):
de ordinul intai, MA(1), ![]()
de ordinul doi, MA(2), ![]()
in raport cu distanta in timp la care se "simte" influenta perturbatiei ;
- modele mixte (autoregresive si de medie mobila), ARMA(p, q), reprezentand o combinatie a ambelor "surse de crestere" (vezi relatia (1.1));
-
modele nestationare autoregresive si de medie mobila, ARIMA(p, d, q), reprezentand o varianta a
modelelor mixte (vezi relatia (1.1)),
prin care se specifica existenta trendului in cadrul seriei cronologice
initiale, marimea "d" indicand
ordinul diferentei care a dus la valori stationare. De regula, diferentele de
ordinul intai dintre termenii seriei ![]() , cel mult diferentele de ordinul doi,
, cel mult diferentele de ordinul doi, ![]() , reusesc sa elimine trendul din date.
, reusesc sa elimine trendul din date.
In tabelul 2.1 sunt prezentate principalele tipuri de modele. In ultima coloana a tabelului este specificata forma concentrata a modelului utilizandu-se operatorul "B" de translatare intr-o perioada din trecut ("backward shift operator"). Rolul unui astfel de operator este descris de egalitatile:
![]()
![]()
![]()
![]()
Modelul AR(2) devine:
![]()
Acesta mai poate fi scris astfel:
![]()
sau, intr-o forma mai concentrata:
![]()
In
continuare, se poate proceda la eliminarea mediei (![]() ) din cadrul valorilor stationare (
) din cadrul valorilor stationare (![]() ), ceea ce este echivalent cu eliminarea parametrului
), ceea ce este echivalent cu eliminarea parametrului ![]() , caz in care modelul, in forma concentrata, devine:
, caz in care modelul, in forma concentrata, devine:
![]()
In cazul modelelor MA(q) operatorul B este utilizat intr-o forma similara.
|
|
Tabelul 2.1
|
Tipul de model |
Forma explicita |
Forma concentrata |
|
Autoregresiv AR(p) |
|
|
|
de medie mobila MA(q) |
|
|
|
Mixt autoregresiv si de medie mobila |
|
|
|
Mixt nestationar |
|
|
O posibilitate de a reda un proces stationar AR(p) se bazeaza pe faptul ca procesul este REDUCTIBIL la
dependente in raport cu ![]() . Astfel, daca consideram procesul AR(1), in care, pentru
. Astfel, daca consideram procesul AR(1), in care, pentru ![]()
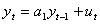 putem afirma ca, la
randul sau,
putem afirma ca, la
randul sau, ![]() , respectiv
, respectiv ![]() etc. Limitandu-ne la
egalitatile privind
etc. Limitandu-ne la
egalitatile privind ![]() si
si ![]() , procedam la inlocuirea lui
, procedam la inlocuirea lui ![]() cu expresia sa in
egalitatea
cu expresia sa in
egalitatea 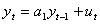 . Rezulta ca:
. Rezulta ca:
![]()
O expresie generala in urma inlocuirilor succesive
privind ![]()
![]() etc. poate fi redata
astfel:
etc. poate fi redata
astfel:
![]() (2.1)
(2.1)
in care, pentru |a|<1, elementele ponderate ale sumei converg catre zero.
Procedand similar, se poate arata ca un proces MA(q) poate fi redat ca un agregat de
termeni ![]() . Astfel, daca consideram ca
. Astfel, daca consideram ca![]() , procesul MA(1) devine
, procesul MA(1) devine ![]() , de unde rezulta ca:
, de unde rezulta ca: ![]() respectiv
respectiv ![]() etc.
etc.
Inlocuind in procesul MA(1) pe ![]() cu expresia sa
cu expresia sa ![]() obtinem:
obtinem:
![]()
Si in acest caz, pentru
|b|<1, ajungem, in urma
inlocuirilor succesive a valorilor ![]() , la valori
, la valori ![]() care converg rapid
catre zero, astfel incat procesul MA(q),
exprimat in raport cu
care converg rapid
catre zero, astfel incat procesul MA(q),
exprimat in raport cu ![]() , sa fie considerat INVERSABIL.
, sa fie considerat INVERSABIL.
In vederea caracterizarii proceselor AR, MA si ARMA avem in vedere media, dispersia si covarianta.
Sa consideram, pentru inceput, modelul autoregresiv in forma sa cea mai simpla, respectiv procesul AR(1):
![]()
unde: ![]() reprezinta variabila
reziduala de natura aleatoare, necorelata, de medie zero si de dispersie
constanta.
reprezinta variabila
reziduala de natura aleatoare, necorelata, de medie zero si de dispersie
constanta.
Pentru un astfel de proces avem in vedere urmatoarele prezumtii:
- sirul
valorilor ![]() (t = 1, 2, ., n)
reprezinta o secventa, un esantion de n
valori, ceea ce face ca parametrii obtinuti sa reprezinte estimari ale
adevaratelor valori;
(t = 1, 2, ., n)
reprezinta o secventa, un esantion de n
valori, ceea ce face ca parametrii obtinuti sa reprezinte estimari ale
adevaratelor valori;
-
densitatea de repartitie este aceeasi in diversele secvente (esantioane) de
valori ![]() , fiind identica cu cea care s-ar obtine pentru ansamblul
valorilor
, fiind identica cu cea care s-ar obtine pentru ansamblul
valorilor ![]() (t = 1, 2, ., N),
obtinandu-se aceeasi medie si dispersie, iar covarianta nedepinzand de
variabila timp ci numai de marimea lag-ului (intarzierii). Asadar, acesta este un
proces slab stationar, caracterizat prin:
(t = 1, 2, ., N),
obtinandu-se aceeasi medie si dispersie, iar covarianta nedepinzand de
variabila timp ci numai de marimea lag-ului (intarzierii). Asadar, acesta este un
proces slab stationar, caracterizat prin:
● Media
![]() (3.1)
(3.1)
intrucat M(u) = 0, iar pentru diversele secvente ![]() media este aceeasi.
media este aceeasi.
In relatia (3.1), daca izolam media, obtinem:
![]()
Daca
consideram ca ![]() , ceea ce ar insemna sa luam in calcul doar
abaterile valorilor
, ceea ce ar insemna sa luam in calcul doar
abaterile valorilor ![]() de la constanta
de la constanta ![]() , obtinem:
, obtinem:
![]()
● Dispersia
![]() (3.2)
(3.2)
intrucat ![]()
![]() , iar
, iar ![]() nu depinde de
nu depinde de ![]()
Daca avem in vedere ca: ![]() , procesul fiind stationar, rezulta ca:
, procesul fiind stationar, rezulta ca:
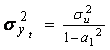 (3.3)
(3.3)
● Covarianta
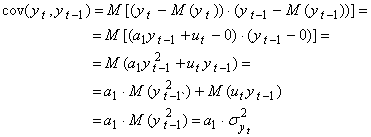 (3.4)
(3.4)
intrucat ![]() si
si ![]() nu sunt corelate,
nu sunt corelate, ![]()
O abordare similara a ![]() conduce la
conduce la ![]() , respectiv:
, respectiv:
![]() (3.5)
(3.5)
O consecinta a caracterizarilor prin prisma mediei,
dispersiei si covariantei se "rasfrange" asupra analizei evolutiei
coeficientilor estimati de autocorelatie, ![]() , pentru k = 1, 2,
3, . Corespunzator relatiei (6.5.5),
coeficientul
, pentru k = 1, 2,
3, . Corespunzator relatiei (6.5.5),
coeficientul ![]() , respectiv estimatia sa, este de forma:
, respectiv estimatia sa, este de forma:
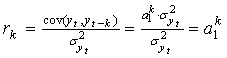 (3.6)
(3.6)
intrucat cov(k), adica ![]() , corespunzator relatiei (3.5).
, corespunzator relatiei (3.5).
Deoarece procesul este stationar, ![]() , aceasta face ca, pe masura ce
, aceasta face ca, pe masura ce ![]() , valorile lui
, valorile lui ![]() sa scada in progresie
geometrica catre zero. In cazul in care
sa scada in progresie
geometrica catre zero. In cazul in care ![]() obtinem estimatii
obtinem estimatii ![]() alternative ca semn,
descriind o involutie de tip "dinti de fierastrau".
alternative ca semn,
descriind o involutie de tip "dinti de fierastrau".
O abordare similara pentru procesul AR(2) conduce la indicatorii:
● Media
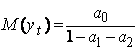 (3.7)
(3.7)
● Dispersia
![]() (3.8)
(3.8)
● Covarianta
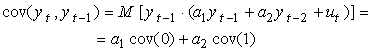 (3.9)
(3.9)
Reamintim faptul ca:
![]()
![]()
Atunci:
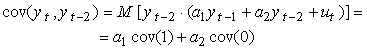 (3.10)
(3.10)
Modul in care evolueaza coeficientii ![]() "tradeaza" existenta
unor analogii in evolutia valorilor
"tradeaza" existenta
unor analogii in evolutia valorilor ![]()
![]()
![]() , care devin tot mai putin evidente pe masura ce distanta in
timp creste. Ca urmare, procesul AR este considerat "de memorie lunga".
, care devin tot mai putin evidente pe masura ce distanta in
timp creste. Ca urmare, procesul AR este considerat "de memorie lunga".
Procesul MA(1) este si el caracterizat de aceeasi indicatori:
● Media
![]() (3.11)
(3.11)
Intrucat
![]()
● Dispersia
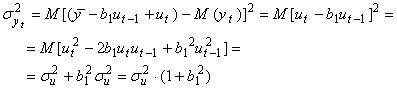
Intrucat
![]() , iar
, iar ![]()
● Covarianta
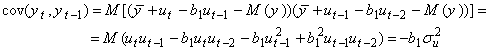
![]() (3.14)
(3.14)
Intrucat, data fiind independenta variabilei reziduale in raport cu propriile sale valori din trecut, covariantele se anuleaza pentru distante dintre valori k > 1.
Estimatia functiei de autocorelatie, ![]() , devine, daca avem in vedere relatiile (3.13) si (3.14), pentru
, devine, daca avem in vedere relatiile (3.13) si (3.14), pentru
![]() (k = 1):
(k = 1):
![]() (3.15)
(3.15)
iar, pentru k > 1, ![]() (vezi relatia (3.14)).
(vezi relatia (3.14)).
Asadar, procesul ![]() se caracterizeaza
printr-o marime semnificativa a coeficientului
se caracterizeaza
printr-o marime semnificativa a coeficientului ![]() dupa care, pentru k > 1, valorile lui
dupa care, pentru k > 1, valorile lui ![]() prezinta o cadere
brusca spre valori nesemnificative (apropiate de zero). Un astfel de proces
poate fi caracterizat ca fiind "de memorie scurta".
prezinta o cadere
brusca spre valori nesemnificative (apropiate de zero). Un astfel de proces
poate fi caracterizat ca fiind "de memorie scurta".
Procedand similar pentru a caracteriza procesul ![]() , ajungem la concluzia ca nivelul estimatiilor lui
, ajungem la concluzia ca nivelul estimatiilor lui ![]() devine nesemnificativ de indata ce k >
2.
devine nesemnificativ de indata ce k >
2.
Procesul ARMA(1)
● Media
![]() (3.16)
(3.16)
Deci ![]() , iar pentru
, iar pentru ![]()
![]()
● Dispersia
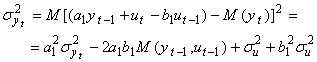 (3.17)
(3.17)
in care ![]()
![]()
Stiind
ca ![]() , iar dispersia este constanta pe diverse segmente de valori ale lui
, iar dispersia este constanta pe diverse segmente de valori ale lui ![]() , vom obtine:
, vom obtine:
![]()
Rezulta ca:
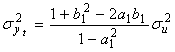 (3.18)
(3.18)
● Covarianta
![]() (3.19)
(3.19)
In cazul in care ![]()
![]() (3.20)
(3.20)
In ceea ce priveste autocorelatia, tinand seama de relatiile (3.18) si (3.19) rezulta ca:
![]() (3.21)
(3.21)
In cazul in care k > 1:
![]() (3.22)
(3.22)
Alaturi
de estimatorii coeficientilor de autocorelatie ![]() prezinta interes,
indeosebi in etapele de specificare si estimare ale modelului, si coeficientii
de autocorelatie partiala (
prezinta interes,
indeosebi in etapele de specificare si estimare ale modelului, si coeficientii
de autocorelatie partiala (![]()
Pentru a obtine valorile acestor coeficienti, asemanatori
in ceea ce priveste interpretarea cu parametri ![]() din modelul
din modelul ![]() , avem in vedere procesul
, avem in vedere procesul ![]()
Corespunzator relatiilor (3.9) si (3.10), ![]() , respectiv
, respectiv ![]() , relatii care, impartite element cu element la dispersie -
cov(0), (reamintindu-ne formula de definire a coeficientului
, relatii care, impartite element cu element la dispersie -
cov(0), (reamintindu-ne formula de definire a coeficientului ![]() ), conduc in cazul relatiei (3.9) la egalitatea:
), conduc in cazul relatiei (3.9) la egalitatea:
![]() (3.23)
(3.23)
Daca avem in vedere faptul ca ![]() , rezulta ca:
, rezulta ca:
![]()
Deci:
![]() (3.24)
(3.24)
In ceea ce priveste relatia (3.10) vom obtine:
![]()
Deci:
![]() (3.25)
(3.25)
Ceea ce conduce la:
![]() (3.26)
(3.26)
Relatiile (3.24)
si (3.26) sunt cunoscute si sub
denumirea de ecuatiile Yule-Walker. Aceste ecuatii ofera posibilitatea
de a obtine necunoscutele ![]() si
si ![]() din procesul
din procesul ![]() pe baza valorilor lui
pe baza valorilor lui ![]() si
si ![]()
Extinzand demersul pentru procesul ![]() , in care:
, in care:
![]()
obtinem in urma impartirii termenilor la cov(0) relatia:
![]() (3.27)
(3.27)
in care ![]() si
si ![]()
Sistemul
de ecuatii care se formeaza in cazul procesului ![]() este urmatorul:
este urmatorul:
![]() Þ
Þ![]()
![]() Þ
Þ ![]() (3.28)
(3.28)
![]() Þ
Þ ![]()
In cadrul sistemului de ecuatii (3.28) parametrii liberi (![]() ) reprezinta coeficientii de autocorelatie partiala.
Generalizand pentru
) reprezinta coeficientii de autocorelatie partiala.
Generalizand pentru 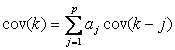 , (k>0) se obtine, in urma
impartirii la cov(0), expresia:
, (k>0) se obtine, in urma
impartirii la cov(0), expresia:
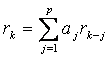 (k = 1, 2, ., K) (3.29)
(k = 1, 2, ., K) (3.29)
Data fiind varietatea modelelor stochastice (vezi tabelul 2.1) este necesara etapa specificarii in care cautam raspuns la urmatoarele intrebari:
- ce tip de model alegem?
- care este ordinul modelului, sau, altfel spus, la ce nivel al indicilor "p" respectiv "q" ne oprim?
Concret, pentru exemplul considerat (vezi tabelul 1.1), urmeaza sa stabilim daca modelul este de tip AR, MA, ARMA sau ARIMA. Intrucat s-a constat in etapa precedenta ca seria prezinta tendinta, iar tendinta a fost eliminata dupa calculul diferentelor de ordin intai, aceste informatii sunt utile specificarii modelului, acesta situandu-se in clasa modelelor nestationare, iar ordinul diferentelor destinate stationarizarii este d = 1. Ar mai urma sa stabilim si nivelul indicilor p si q pentru a defini complet forma modelului AR(p) si/sau MA(q).
Pentru a da raspuns intrebarilor formulate si, implicit, pentru a specifica forma modelului, avem in vedere unele considerente teoretice prezentate in paragraful precedent.
Criteriile se bazeaza pe urmatoarele "semnale":
a) functia de autocorelatie si analiza modificarilor coeficientilor de autocorelatie pentru k = 1, 2, .;
b)
analiza comparativa a evolutiei
coeficientilor de autocorelatie ![]() si a coeficientilor de
autocorelatie partiala
si a coeficientilor de
autocorelatie partiala ![]() pentru k = 1, 2 ,.;
pentru k = 1, 2 ,.;
c) aprecierea posibilitatilor de evolutie in timp ale fenomenului economic tinand seama de particularitatile acestuia, conjunctura economica si schimbarile in trecut si viitor ale variabilelor exogene, precum si de rezultatele unor studii similare anterioare (experienta si intuitia econometricianului detin un rol important).
Pentru o cat mai corecta specificare a modelului este necesar ca cel putin doua dintre cele trei criterii sa fie luate in considerare.
Inainte de a aborda modalitatea de aplicare a criteriilor este necesar sa
mentionam ca functia de autocorelatie se refera la intensitatea analogiei
dintre ![]() si
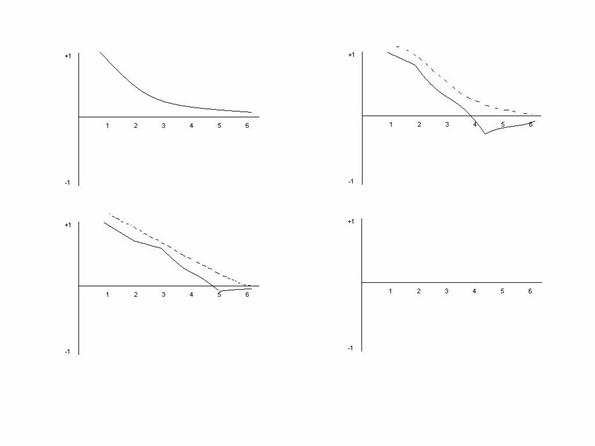
si ![]() pentru k = 1, 2,. Corelograma reda sugestiv
modificarea coeficientilor de autocorelatie pe domeniul lor de definitie situat
intre
pentru k = 1, 2,. Corelograma reda sugestiv
modificarea coeficientilor de autocorelatie pe domeniul lor de definitie situat
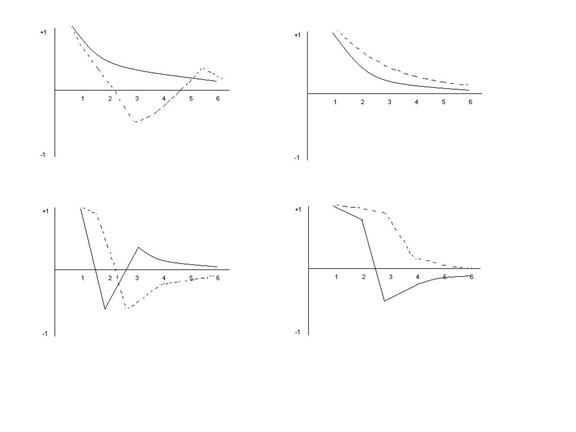
intre ![]() , pentru marimi ale lag-ului care nu depasesc, de regula, 6-7
intervale (vezi figurile 4.1 - 4.7).
, pentru marimi ale lag-ului care nu depasesc, de regula, 6-7
intervale (vezi figurile 4.1 - 4.7).
Pentru etapa specificarii prezinta importanta doar marimea coeficientilor nu si semnul acestora astfel incat pozitia lor pe grafic in raport cu axa orizontala mai putin importa.
Coeficientii
de autocorelatie partiala ![]() masoara gradul de
asociere dintre
masoara gradul de
asociere dintre ![]() si
si ![]() in ipoteza in care
influenta nivelului din trecut pentru orice lag diferit de k este mentinut constant. O astfel de izolare a influentei este
importanta pentru a indica cel mai adecvat model ARMA destinat prognozei.
in ipoteza in care
influenta nivelului din trecut pentru orice lag diferit de k este mentinut constant. O astfel de izolare a influentei este
importanta pentru a indica cel mai adecvat model ARMA destinat prognozei.
In decursul specificarii modelului
prin prisma celor trei criterii pot fi intalnite situatiile la care ne vom
referi in cele ce urmeaza:
1)
Existenta unei tendinte evolutive - aspect semnalat de faptul ca coeficientii
de autocorelatie estimati ![]()
![]()
![]() , eventual
, eventual ![]()
![]() , prezinta nivele semnificativ diferite de zero ce descresc
lent. Asa cum am aratat intr-un paragraf anterior, este necesar sa eliminam
tendinta calculand diferentele dintre termenii seriei cronologice. Tendinta
poate fi complet eliminata dupa calculul diferentelor de ordinul intai (d = 1) sau, ceea ce mai rar se intampla,
a diferentelor de ordinul doi (d = 2)
sau mai mare.
, prezinta nivele semnificativ diferite de zero ce descresc
lent. Asa cum am aratat intr-un paragraf anterior, este necesar sa eliminam
tendinta calculand diferentele dintre termenii seriei cronologice. Tendinta
poate fi complet eliminata dupa calculul diferentelor de ordinul intai (d = 1) sau, ceea ce mai rar se intampla,
a diferentelor de ordinul doi (d = 2)
sau mai mare.
2) Procesul este pur autoregresiv (AR) daca avem in vedere criteriile:
a)
coeficientii ![]() descresc pentru k = 2, 3, 4, . fie in progresie
geometrica, fie descriind conturul dintilor de ferastrau ( vezi figura 4.1).
Ordinul procesului autoregresiv este intai daca descresterea este rapida,
respectiv este egal cu distanta dintre varfurile dintilor de ferastrau in cazul
evolutiei in zig-zag. In cazul seriilor ce prezinta sezonalitate, coeficientii
prezinta nivele semnificative la distante egale cu numarul de unitati de timp
(luni, trimestre) dintr-un an;
descresc pentru k = 2, 3, 4, . fie in progresie
geometrica, fie descriind conturul dintilor de ferastrau ( vezi figura 4.1).
Ordinul procesului autoregresiv este intai daca descresterea este rapida,
respectiv este egal cu distanta dintre varfurile dintilor de ferastrau in cazul
evolutiei in zig-zag. In cazul seriilor ce prezinta sezonalitate, coeficientii
prezinta nivele semnificative la distante egale cu numarul de unitati de timp
(luni, trimestre) dintr-un an;
b)
coeficientii ![]() descresc in progresie
geometrica, in timp ce coeficientii
descresc in progresie
geometrica, in timp ce coeficientii ![]() descresc brusc dupa o
marime a lag-ului egala cu unu, caz in care ordinul procesului autoregresiv este
unu, sau dupa o marime a lag-ului egala cu doi, caz in care ordinul procesului
autoregresiv este doi etc. (fig. 4.2, si 4.3);
descresc brusc dupa o
marime a lag-ului egala cu unu, caz in care ordinul procesului autoregresiv este
unu, sau dupa o marime a lag-ului egala cu doi, caz in care ordinul procesului
autoregresiv este doi etc. (fig. 4.2, si 4.3);
c) fenomenul economic este dependent de acumulari, de experienta din trecut, avand deci un pronuntat caracter inertial. Se recomanda optiunea pentru un model autoregresiv (pur), al carui ordin rezulta, conform celor aratate, din "citirea" corelogramei.
Cazul evolutiilor pur autoregresive fiind destul de rar intalnit, nu trebuie exclusa posibilitatea unui model mixt (ARMA).
3) Procesul este caracterizat ca fiind de medie mobila (MA) daca:
a)
coeficientii de autocorelatie ![]() se apropie brusc de
zero dupa k unitati de timp. Ordinul
modelului de medie mobila este egal cu k-1 ;
se apropie brusc de
zero dupa k unitati de timp. Ordinul
modelului de medie mobila este egal cu k-1 ;
b)
nivelul coeficientilor de autocorelatie ![]() se apropie brusc de
zero, in timp ce coeficientii de autocorelatie partiala
se apropie brusc de
zero, in timp ce coeficientii de autocorelatie partiala ![]() scad in proportie
geometrica (fig. 4.4)
scad in proportie
geometrica (fig. 4.4)
Ordinul modelului de medie mobila este dat de marimea
maxima a indicelui k pentru care ![]() prezinta o valoare
semnificativa.
prezinta o valoare
semnificativa.
c) variabila economica este sensibila in timp la modificarile de amploare ale unor variabile exogene (pret, oferta, calamitati etc.) intrucat ele genereaza abateri accidentale de la media evolutiei, abateri care se repercuteaza in timp, scazand treptat in influenta.
Desi se recomanda un model de medie mobila, nici in acest caz nu trebuie exclusa posibilitatea de a reprezenta mai bine evolutia in timp prin modelul mixt (ARMA).
4) Procesul este considerat de tip ARMA daca:
![]() a) coeficientii de
autocorelatie scad partial treptat in intensitate, apropiindu se apoi
rapid de nivele nesemnificative dupa k
unitati de timp. Pentru a stabili ordinul modelului AR avem in vedere marimea
indicelui k pentru care coeficientii se mentin la nivele relativ mari; pentru a
stabili ordinul modelului MA, avem in vedere marimea indicelui k pentru care coeficientul
a) coeficientii de
autocorelatie scad partial treptat in intensitate, apropiindu se apoi
rapid de nivele nesemnificative dupa k
unitati de timp. Pentru a stabili ordinul modelului AR avem in vedere marimea
indicelui k pentru care coeficientii se mentin la nivele relativ mari; pentru a
stabili ordinul modelului MA, avem in vedere marimea indicelui k pentru care coeficientul ![]() devine nesemnificativ,
caz in care ordinul partii de medie
mobila din modelul mixt este q = k - 1;
devine nesemnificativ,
caz in care ordinul partii de medie
mobila din modelul mixt este q = k - 1;
b) atat
coeficientii de autocorelatie ![]() cat si coeficientii de
autocorelatie partiala
cat si coeficientii de
autocorelatie partiala ![]() scad continuu,
apropiindu-se de zero (vezi figurile 4.6 si 4.7), fara a se observa o scadere
brusca la niciunul dintre ei. Ordinul partii autoregresive a modelului mixt
este semnalata de nivelul pentru care coeficientii
scad continuu,
apropiindu-se de zero (vezi figurile 4.6 si 4.7), fara a se observa o scadere
brusca la niciunul dintre ei. Ordinul partii autoregresive a modelului mixt
este semnalata de nivelul pentru care coeficientii ![]() prezinta nivele cat de
cat semnificative, iar ordinul partii de medie mobila din modelul mixt este dat
de nivelul maxim al indicelui k
pentru care coeficientii
prezinta nivele cat de
cat semnificative, iar ordinul partii de medie mobila din modelul mixt este dat
de nivelul maxim al indicelui k
pentru care coeficientii ![]() sunt suficient de
mari;
sunt suficient de
mari;
c) fenomenul descris de seria de timp este tributar atat realizarilor sale din trecut cat si abaterilor accidentale datorate unor modificari de amploare ale variabilelor exogene.
Modelul autoregresiv si de medie mobila (mixt) ARMA reprezinta "cazul general" si este considerat cel mai indicat pentru elaborarea de prognoze in economie atunci cand nu este cunoscuta (nu avem date) evolutia variabilelor exogene.
Modelul ARMA este deseori rezultatul specificarii pentru variabila stationara (prin diferente de ordinul d) si care, in forma originala, prezinta tendinta (vezi situatia 1).
Acest aspect este specificat atat prin denumirea de model nestationar autoregresiv si de medie mobila cat si prin simbolul ARIMA utilizat. Acest simbol este urmat de nivelul indicilor:
- p = ordinul partii autoregresive a modelului;
- d = ordinul diferentelor care au condus
la valori ale lui ![]() stationare;
stationare;
- q = ordinul partii de medie mobila a modelului.
Astfel,
pentru a semnala un model care se refera la o serie adusa la forma stationara
dupa calculul diferentelor de ordinul intai, fiind autoregresiva de ordinul
intai si de medie mobila de ordinul doi, notam cu: ![]() sau
sau ![]() . Ecuatia unui astfel de model este:
. Ecuatia unui astfel de model este:
![]() (4.1)
(4.1)
unde:
![]()
Exemple
1) Pentru exemplul considerat (vezi tabelul 1.1) clasa de modele indicata
este cea nestationara intrucat seria cronologica, in forma initiala, prezinta
tendinta. Intrucat tendinta a fost eliminata dupa calculul diferentelor de
ordinul intai, iar caracteristicile seriei stationare astfel obtinute sunt
conforme indeosebi modelului mixt (autocorelatie relativ mare pentru k=1, devenind nesemnificativa pentru k = 2, iar scaderea spre nivelul zero a
coeficientilor ![]() si
si ![]() pentru k = 1, 2, 3, . este treptata), modelul a
fost specificat drept nestationar, autoregresiv de ordinul unu si de medie
mobila de ordinul unu. Deci, modelul ARIMA(1,1,1)
este redat explicit astfel:
pentru k = 1, 2, 3, . este treptata), modelul a
fost specificat drept nestationar, autoregresiv de ordinul unu si de medie
mobila de ordinul unu. Deci, modelul ARIMA(1,1,1)
este redat explicit astfel:
![]() (4.2)
(4.2)
Continuam exemplificarile referindu ne la serii ceva mai lungi de date, asa cum sunt cele prezentate in Capitolul VI (aplicatia din partea finala a capitolului).
2) Astfel, pentru seria Vt:
au fost obtinute
estimatiile ![]()
![]()
![]() Coeficientii de
autocorelatie partiala rezulta din sistemul de ecuatii (3.28):
Coeficientii de
autocorelatie partiala rezulta din sistemul de ecuatii (3.28):
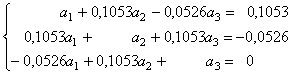
pentru care:![]()
![]()
![]()
In urma aplicarii testelor Bartlett, Q, LB a rezultat ca
ipoteza nula (![]() ) este confirmata, seria
) este confirmata, seria ![]() fiind de tip aleator
(stationara). Daca ne propunem sa specificam modelul pentru o astfel de serie,
constatam ca, atat
fiind de tip aleator
(stationara). Daca ne propunem sa specificam modelul pentru o astfel de serie,
constatam ca, atat ![]() cat si
cat si ![]() , pentru k = 1, 2,
3, prezinta valori nesemnificative, apropiate de zero, neincadrandu se in
tipologia modelelor stochastice.
, pentru k = 1, 2,
3, prezinta valori nesemnificative, apropiate de zero, neincadrandu se in
tipologia modelelor stochastice.
In cazul seriei Zt: 1 1 2 1 2 2 2 3 3 3 3 3 4 4 5 5 5 5 6 5 6 6 7 8 8 au rezultat: ![]()
![]()
![]() Valorile lui
Valorile lui ![]() scad lent, ceea ce
semnaleaza ca seria este omogena, nestationara, aspect rezultat si in urma
aplicarii testelor Bartlett, Q, LB.
scad lent, ceea ce
semnaleaza ca seria este omogena, nestationara, aspect rezultat si in urma
aplicarii testelor Bartlett, Q, LB.
In urma determinarii diferentelor de ordinul intai s-a
obtinut sirul ![]() cu valorile: 0 1 -1 1 0 0 1 0 0 0 1 0 1 0 0 0 1 -1 1 0 1 1 0.
cu valorile: 0 1 -1 1 0 0 1 0 0 0 1 0 1 0 0 0 1 -1 1 0 1 1 0.
Coeficientii ![]() in acest caz sunt:
in acest caz sunt: ![]()
![]()
![]() . Coeficientii
. Coeficientii ![]() rezulta din sistemul
de ecuatii (3.28):
rezulta din sistemul
de ecuatii (3.28):
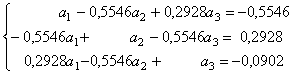
obtinandu-se:
![]()
![]()
![]()
Involutia coeficientilor ![]() , coroborata cu "caderea" coeficientilor
, coroborata cu "caderea" coeficientilor ![]() pentru
pentru ![]() , sugereaza, in ce priveste specificarea, un model AR(1),
eventual ARMA(1,1).
, sugereaza, in ce priveste specificarea, un model AR(1),
eventual ARMA(1,1).
Mentionam ca, in ceea ce priveste etapa specificarii modelului stochastic, ne situam pe un "teren nesigur" in care, alaturi de criteriile mentionate, un rol deosebit il are si experienta econometricianului. Se recomanda optiunea pentru doua, trei variante de specificare, urmand ca, dupa parcurgerea etapelor de estimare si verificare, sa se aprecieze care dintre variante este mai indicata pentru obtinerea de prognoze.
Exprimarea cea mai prudenta a modelului stochastic are in vedere varianta ARMA sau ARIMA (daca exista trend in date). In acest fel, este eliminat riscul "scoaterii din joc", printr-o neinspirata definire a modelului, a acelor factori care se modifica imprevizibil, declansand erori de prognoza (partea MA), sau a factorilor inertiali sau care produc acumulari (partea AR).
modelelor stochastice (Box - Jenkins)
Obtinerea de estimatii de maxima verosimilitate pentru
parametrii "a" si "b" din modelele stochastice
autoregresive si de medie mobila implica minimizarea sumei patratelor erorilor
(![]() ). Ipoteza repartitiei normale a erorilor (perturbatiei) face
ca estimatiile de maxima verosimilitate sa fie identice cu estimatiile obtinute
prin M.C.M.M.P.
). Ipoteza repartitiei normale a erorilor (perturbatiei) face
ca estimatiile de maxima verosimilitate sa fie identice cu estimatiile obtinute
prin M.C.M.M.P.
Intrucat secventa MA a modelului ARMA induce
neliniaritatea in raport cu parametrii ![]() , este necesara utilizarea unui algoritm extrem de laborios a
carui desfasurare incercam sa o prezentam in conditii cat mai apropiate de
cerintele elaborarii unui program pentru prelucrarea electronica a datelor.
, este necesara utilizarea unui algoritm extrem de laborios a
carui desfasurare incercam sa o prezentam in conditii cat mai apropiate de
cerintele elaborarii unui program pentru prelucrarea electronica a datelor.
Pentru inceput, ne referim la cazul mai simplu al
modelului autoregresiv (AR). In vederea estimarii parametrilor se recomanda
aplicarea M.C.M.M.P. Asadar, urmeaza sa obtinem estimatorii ![]() pentru care expresia
urmatoare este minima:
pentru care expresia
urmatoare este minima:
![]() (5.1)
(5.1)
Asa cum aratam in Capitolul VII atunci cand am abordat
problema modelelor cu lag distribuit (vezi relatia (7.1.2)), existenta dependentei dintre variabila![]() si perturbatie, ca si existenta coliniaritatii intre
si perturbatie, ca si existenta coliniaritatii intre ![]() si
si ![]() , fac ca estimatorii sa nu fie eficienti si nici suficient de
stabili. Pentru a evita aceste efecte nedorite apelam la metoda variabilelor
instrumentale sau la metode iterative, intre care cea destinata rezolvarii unui
sistem de ecuatii de tip Yule - Walker este frecvent recomandata
, fac ca estimatorii sa nu fie eficienti si nici suficient de
stabili. Pentru a evita aceste efecte nedorite apelam la metoda variabilelor
instrumentale sau la metode iterative, intre care cea destinata rezolvarii unui
sistem de ecuatii de tip Yule - Walker este frecvent recomandata
Astfel, pentru un model AR(2) ecuatiile Yule - Walker se prezinta astfel :
![]() (5.2)
(5.2)
![]() (5.3)
(5.3)
Exemplu
In
vederea exemplificarii procedeului de estimare prezentam urmatorul sir de
valori ![]() pentru 12 perioade
succesive:
pentru 12 perioade
succesive:
![]() : 2 3 3 3 3 3 2 6 6 5 5 7
: 2 3 3 3 3 3 2 6 6 5 5 7 ![]()
Intrucat estimatorii coeficientilor de autocorelatie
sunt: ![]()
![]()
![]()
![]() , modelul a fost specificat ca fiind de tip AR(2).
Estimatorii parametrilor rezulta din relatiile (5.2) si (5.3) astfel:
, modelul a fost specificat ca fiind de tip AR(2).
Estimatorii parametrilor rezulta din relatiile (5.2) si (5.3) astfel:
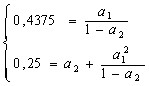
pentru care ![]()
![]() , iar parametrul
, iar parametrul ![]() poate fi corect
aproximat de
poate fi corect
aproximat de ![]()
In cazurile in care modelul stochastic include si elemente de medie mobila, fiind de tip ARMA, ARIMA sau MA, utilizarea metodei celor mai mici patrate in varianta obisnuita nu este recomandata intrucat:
-
modelul este, in general, neliniar din perspectiva parametrilor, aspect evident
daca avem in vedere relatia ![]()
-
ecuatia modelului presupune, in vederea obtinerii de estimatii, cunoasterea
unor valori din trecut (![]() ) pentru care nu dispunem de date. Ca urmare, sunt necesare
initializari si metode iterative.
) pentru care nu dispunem de date. Ca urmare, sunt necesare
initializari si metode iterative.
Estimarea,
in principiu, se bazeaza pe ipoteza conform careia variabila reziduala urmeaza
o repartitie normala cu valori ![]() independente.
Estimarea de maxima verosimilitate a parametrilor
independente.
Estimarea de maxima verosimilitate a parametrilor ![]() presupune minimizarea
sumei:
presupune minimizarea
sumei:
![]()
Dintre metodele de estimare recomandate pentru modelele neliniare in raport cu parametrii intereseaza procedeul adecvat situatiei in care unele valori din trecut, necunoscute, apar in formula rezultata in urma specificarii.
In cele
ce urmeaza ne vom referi la un procedeu de estimare recomandat pentru modelul
ARMA intrucat acest tip de model reprezinta forma generala a modelelor
stochastice. Pentru a se ajunge in cazul unui astfel de model la estimatori ai
parametrilor ![]() care sa indeplineasca
conditia
care sa indeplineasca
conditia ![]() se recomanda
utilizarea unui procedeu iterativ [11]. In principiu, un astfel de procedeu
presupune:
se recomanda
utilizarea unui procedeu iterativ [11]. In principiu, un astfel de procedeu
presupune:
- initializarea parametrilor cu valori bazate
pe coeficientii ![]()
-
dezvoltarea expresiei concentrate a modelului ![]() in serie Taylor in
jurul initializarilor stabilite pentru parametrii, si retinerea primilor doi
termeni dintr-o astfel de dezvoltare, ceea ce permite obtinerea de ecuatii
liniare;
in serie Taylor in
jurul initializarilor stabilite pentru parametrii, si retinerea primilor doi
termeni dintr-o astfel de dezvoltare, ceea ce permite obtinerea de ecuatii
liniare;
- obtinerea de estimatii ale parametrilor ecuatiilor liniare folosind in acest scop M.C.M.M.P.;
-
comparatii ale estimatiilor astfel obtinute cu cele rezultate in anterioara
iteratie (pentru inceput avem in vedere initializarile bazate pe coeficientii ![]() ) in scopul aprecierii realizarii convergentei;
) in scopul aprecierii realizarii convergentei;
- daca convergenta este constatata, ultimele estimatii sunt cele valabile, iar daca estimatiile nu converg, se inlocuiesc solutiile iteratiei precedente cu cele obtinute in ultima iteratie si se reia procesul de la cea de-a doua etapa (dezvoltare in serie Taylor, aplicarea M.C.M.M.P. etc.).
Pentru a reda mai detaliat etapele din perspectiva programarii acestora avem in vedere modelul ARIMA(1,1,1). Formulele-cheie privind alte modele frecvent intalnite, ARMA(1,2), ARMA(2,2), vor completa demersul.
Calcule preliminarii:
pentru serii nestationare procedam la eliminarea tendintei;
pentru simplificarea calculelor eliminam media din date.
Sa exemplificam aceasta etapa reluand datele din tabelul 1.1
Tabel 5.1
|
Valori originale |
5 6 8 9 13 15 16 18 20 22 |
|
|
Valori stationare |
3 1 2 1 4 2 1 2 2 2 |
|
|
Valori stationare
minus media |
1 -1 0 -1 2 0 -1 0 0 0 |
2. Exprimam modelul in forma concentrata servindu-ne de operatorul de translatare in trecut (B).
Astfel, modelul ARIMA(1,1,1) care, dupa stationarizare,
devine ARMA(1,1) este exprimat, dupa eliminarea mediei, de relatia ![]() Introducand operatorul
"B" modelul devine:
Introducand operatorul
"B" modelul devine:
![]()
De unde:
![]() (5.4)
(5.4)
Forme concentrate pentru alte tipuri de modele:
- forma concentrata pentru ARMA(1,2)
![]() (5.5)
(5.5)
pentru ARMA(2,1)
![]() (5.6)
(5.6)
pentru ARMA(2,2)
![]() (5.7)
(5.7)
3.
Initializam parametrii pe baza estimatiilor coeficientilor de autocorelatie ![]() . Astfel, in cazul modelului ARMA(1,1):
. Astfel, in cazul modelului ARMA(1,1):
![]()
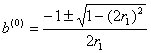
Intr-adevar,
daca avem in vedere relatiile (3.6)
si (3.15) atunci, intrucat pentru
AR(1), ![]() , iar pentru partea
, iar pentru partea ![]()
![]() . Acest din urma raport conduce la ecuatia
. Acest din urma raport conduce la ecuatia ![]() , in care parametrul b1
este necunoscut.
, in care parametrul b1
este necunoscut.
Mentionam
ca, in vederea initializarilor putem avea in vedere, la fel de bine, si
coeficientii de autocorelatie partiala ![]()
Atribuim,
de asemenea, valoarea zero acelor nivele ale variabilei care sunt "in afara
cadrului": ![]()
![]()
![]()
![]()
In
exemplul considerat, intrucat ![]() , respectiv, dupa eliminarea mediei, valorile expuse in
tabelul 5.1 - randul 3 vor conduce la obtinerea aceluiasi coeficient
, respectiv, dupa eliminarea mediei, valorile expuse in
tabelul 5.1 - randul 3 vor conduce la obtinerea aceluiasi coeficient ![]() . Ca urmare, initializarea presupune:
. Ca urmare, initializarea presupune:
![]()
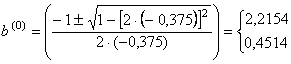
Dintre
cele doua valori obtinute pentru ![]() alegem
alegem ![]()
4.
Dezvoltam in serie Taylor expresia ![]() in jurul
initializarilor
in jurul
initializarilor ![]()
![]() si retinem doar primii
doi termeni din intreaga dezvoltare .
Deci:
si retinem doar primii
doi termeni din intreaga dezvoltare .
Deci:
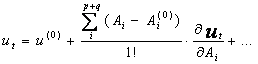 (5.8)
(5.8)
unde:
![]() = vectorul parametrilor necunoscuti
= vectorul parametrilor necunoscuti ![]()
![]() = vectorul initializarilor privind parametrii
= vectorul initializarilor privind parametrii![]()
Derivata partiala in raport cu "a" este egala cu:
![]()
Intrucat:
![]()
![]()
Rezulta urmatoarea ecuatie liniara:
![]() (5.9)
(5.9)
Derivata partiala in raport cu b : ![]() conduce la cea de-a
doua ecuatie:
conduce la cea de-a
doua ecuatie:
![]() (5.10)
(5.10)
Ecuatia (5.8) poate fi redata astfel:
![]() (5.11)
(5.11)
Izoland necunoscutele a si b in dreapta semnului egalitatii obtinem:
![]() (5.12)
(5.12)
urmand ca, in etapa
urmatoare, sa calculam ![]() pe baza valorilor
variabilei
pe baza valorilor
variabilei![]() (in varianta stationarizata, avand media eliminata) si a
initializarilor mentionate in etapa a treia.
(in varianta stationarizata, avand media eliminata) si a
initializarilor mentionate in etapa a treia.
Mentionam ecuatiile liniare obtinute, intr-un mod similar procedeului descris pentru ARMA(1,1), pentru modelele:
ARMA(1,2)
![]() (5.13)
(5.13)
![]()
![]()
ARMA(2,1)
![]() (5.16)
(5.16)
![]() (5.17)
(5.17)
![]() (5.18)
(5.18)
5.
Calculam valorile ![]() luand in considerare
initializarile si valorile variabilei
luand in considerare
initializarile si valorile variabilei ![]() din tabelul 5.1 -
randul 3.
din tabelul 5.1 -
randul 3.
Relatiile (5.9) si (5.10) sunt cele care ne stau in atentie:
![]()
![]()
![]()
![]()
![]()
![]()
De asemenea, se procedeaza la calculul valorilor ![]()
![]()
Deci:
![]()
![]()
![]()
![]()
In exemplul considerat:
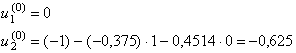
In final, stabilim nivelul valorilor din stanga egalitatii relatiei (5.12) in urma unor operatiuni de insumare pentru t = 1, 2, 3, . Asadar, pentru momentul t, obtinem:
![]()
6. Intrucat, in urma celei
de-a cincea etape, am ajuns la un model liniar de regresie clasic pentru care,
in cazul ARMA(1,1) am determinat valori privind "factorii" x si z si "efectul" G, urmeaza sa aplicam M.C.M.M.P. in
forma obisnuita, obtinand estimatorii pe care ii simbolizam cu ![]() . Sa presupunem ca am
obtinut
. Sa presupunem ca am
obtinut ![]()
7.
Comparam estimatiile obtinute in cea de-a sasea etapa cu estimatiile
anterioare, obtinute prin M.C.M.M.P. sau
initializate. In cazul nostru, comparam marimile ![]() cu initializarile
cu initializarile ![]() . Daca constatam ca marimile nu converg spre nivele stabile,
inlocuim estimatiile anterioare cu ultimele estimatii obtinute si reluam
procesul iterativ incepand cu cea de-a cincea etapa. Asadar, atribuim
parametrilor a si b cele mai recente estimatii rezultate
din aplicarea M.C.M.M.P., in cazul nostru a
= 0,3 si b = -0,2 si revenim la cea
de-a cincea etapa procedand la calculul valorilor
. Daca constatam ca marimile nu converg spre nivele stabile,
inlocuim estimatiile anterioare cu ultimele estimatii obtinute si reluam
procesul iterativ incepand cu cea de-a cincea etapa. Asadar, atribuim
parametrilor a si b cele mai recente estimatii rezultate
din aplicarea M.C.M.M.P., in cazul nostru a
= 0,3 si b = -0,2 si revenim la cea
de-a cincea etapa procedand la calculul valorilor ![]() pe baza acestor nivele
ale parametrilor. Apoi, in cea de-a sasea etapa, se aplica M.C.M.M.P. si se
obtine alt set de estimatii
pe baza acestor nivele
ale parametrilor. Apoi, in cea de-a sasea etapa, se aplica M.C.M.M.P. si se
obtine alt set de estimatii ![]() . Evident, comparatia se reia de asta data intre
. Evident, comparatia se reia de asta data intre ![]() si
si ![]() . Sa presupunem ca, dupa cateva astfel de iteratii,
convergenta estimatiilor s-a realizat pentru valorile
. Sa presupunem ca, dupa cateva astfel de iteratii,
convergenta estimatiilor s-a realizat pentru valorile ![]() si
si ![]() . In acest caz, aceste din urma nivele sunt considerate
estimatiile cautate.
. In acest caz, aceste din urma nivele sunt considerate
estimatiile cautate.
Pentru
procesele ARMA in care ![]() si
si ![]() metoda prezentata este
cu deosebirea indicata. Pentru procese de ordin mai mare, din fericire mai rar
intalnite in aplicatii, metoda este nu numai laborioasa dar, in mod frecvent,
convergenta se realizeaza greu, ceea ce
face deseori necesara reevaluarea initializarilor din etapa a treia. Daca dupa
mai multe incercari convergenta nu are loc, este indicat sa se incerce o noua
specificare a modelului. Aceasta se intampla chiar si pentru modele mixte de
ordin
metoda prezentata este
cu deosebirea indicata. Pentru procese de ordin mai mare, din fericire mai rar
intalnite in aplicatii, metoda este nu numai laborioasa dar, in mod frecvent,
convergenta se realizeaza greu, ceea ce
face deseori necesara reevaluarea initializarilor din etapa a treia. Daca dupa
mai multe incercari convergenta nu are loc, este indicat sa se incerce o noua
specificare a modelului. Aceasta se intampla chiar si pentru modele mixte de
ordin ![]()
![]() in cazurile in care
initializarile nu au fost cele mai potrivite sau in situatiile in care
specificarea modelului a fost dificila datorita ambiguitatii evolutiei
coeficientilor de autocorelatie.
in cazurile in care
initializarile nu au fost cele mai potrivite sau in situatiile in care
specificarea modelului a fost dificila datorita ambiguitatii evolutiei
coeficientilor de autocorelatie.
Parcurgerea etapelor destinate specificarii modelului si estimarii parametrilor scoate in evidenta, in afara volumului mare de calcule pe care il presupun tehnicile Box - Jenkins, comparativ cu alte metode (vezi Capitolele VI si VII) si rolul relativ mare pe care il detin experienta si inspiratia econometricianului. Aceasta apare mai pregnant in etapa de specificare, dar, daca avem in vedere posibilitatea de a alege intre metodele de estimare (cazul modelelor AR) ca si posibilitatea de a modifica initializarile parametrilor, rezulta ca intuitia, experienta au un rol deosebit in etapa estimarii.
Ca urmare, verificarea modelului se refera nu atat la testarea semnificatiei, sau nu numai la aceasta, ci si la calitatea modelului de a reproduce caracterul inertial si de asimilare a socurilor care apar in evolutia fenomenelor economice in timp. Acestei etape ii revine deci un rol de "control de calitate" bine determinat in intregul demers de pregatire si elaborare a previziunilor.
Verificarea
modelului, inainte de utilizarea sa pentru elaborarea de prognoze presupune
analiza corelogramei valorilor coeficientilor de autocorelatie ![]() elaborata pentru
valorile
elaborata pentru
valorile ![]() generate prin modelul
adoptat (valori stationare obtinute din model). Daca intre corelograma
initiala, utilizata in etapa de specificare, privind valorile empirice
stationare
generate prin modelul
adoptat (valori stationare obtinute din model). Daca intre corelograma
initiala, utilizata in etapa de specificare, privind valorile empirice
stationare ![]() , si corelograma coeficientilor de autocorelatie bazata pe
valorile
, si corelograma coeficientilor de autocorelatie bazata pe
valorile ![]() generate de model
exista o asemanare evidenta, astfel incat analiza ultimei corelograme ar
conduce la aceeasi specificare a modelului, consideram ca modelul este valid.
In cazul in care corelogramele difera foarte mult, se realizeaza revizuirea
initializarilor atribuite parametrilor. Daca modificarea initializarilor nu are
efectele scontate, se procedeaza la respecificarea modelului in sensul ca se modifica ordinul
modelului fie pentru secventa sa autoregresiva, fie pentru cea de medie mobila,
fie pentru ambele. Nu poate fi exclusa nici modificarea tipului de model (in
loc de a utiliza un model MA(q) sa
avem in vedere un model ARMA sau, mai rar, un model AR(q)).
generate de model
exista o asemanare evidenta, astfel incat analiza ultimei corelograme ar
conduce la aceeasi specificare a modelului, consideram ca modelul este valid.
In cazul in care corelogramele difera foarte mult, se realizeaza revizuirea
initializarilor atribuite parametrilor. Daca modificarea initializarilor nu are
efectele scontate, se procedeaza la respecificarea modelului in sensul ca se modifica ordinul
modelului fie pentru secventa sa autoregresiva, fie pentru cea de medie mobila,
fie pentru ambele. Nu poate fi exclusa nici modificarea tipului de model (in
loc de a utiliza un model MA(q) sa
avem in vedere un model ARMA sau, mai rar, un model AR(q)).
Pentru datele prezentate in tabelul 5.1 am optat pentru un model ARIMA(1,1,1). Valorile generate de model, in varianta stationarizata, in care includem insa si media, rezulta astfel:
![]()
unde:
![]()
![]()
Obtinerea
valorilor lui![]() ca si rezultatele comparatiei
dintre
ca si rezultatele comparatiei
dintre ![]() si nivelele empirice
si nivelele empirice ![]() (tabelul 5.1- randul 2), sunt prezentate in cele ce urmeaza:
(tabelul 5.1- randul 2), sunt prezentate in cele ce urmeaza:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Seria originala, ![]() , rezulta urmand un proces invers celui obtinerii de valori
stationarizate. Asadar, intrucat
, rezulta urmand un proces invers celui obtinerii de valori
stationarizate. Asadar, intrucat ![]() (vezi tabelul 5.1),
rezulta ca
(vezi tabelul 5.1),
rezulta ca ![]() . Se obtin astfel urmatoarele valori:
. Se obtin astfel urmatoarele valori:
![]()
![]()
![]()
![]()
Pentru valorile lui ![]() astfel obtinute se calculeaza coeficientii de autocorelatie
astfel obtinute se calculeaza coeficientii de autocorelatie ![]() (k = 1, 2, 3, 4, 5), iar reprezentarea grafica a acestora se compara
cu cea a coeficientilor
(k = 1, 2, 3, 4, 5), iar reprezentarea grafica a acestora se compara
cu cea a coeficientilor ![]() , calculati pentru datele empirice din tabelul 5.1 - randul
2. Daca asemanarea graficelor este evidenta, astfel incat si pe baza valorilor
lui
, calculati pentru datele empirice din tabelul 5.1 - randul
2. Daca asemanarea graficelor este evidenta, astfel incat si pe baza valorilor
lui![]() ajungem la aceeasi concluzie privind tipul si ordinul
modelului (ARMA(1,1,1)), modelul este valid[10].
ajungem la aceeasi concluzie privind tipul si ordinul
modelului (ARMA(1,1,1)), modelul este valid[10].
O alta modalitate de verificare are in vedere analiza "resturilor", adica analiza variabilei reziduale. In cazul unui model performant (bine specificat, corect estimat), valorile variabilei reziduale sunt aleatoare si necorelate, astfel incat coeficientii de autocorelatie calculati pentru astfel de valori sunt nesemnificativi. Testul dezvoltat de Ljung si Box are in vedere valoarea calculata, Q, care se obtine astfel :
![]() (6.1)
(6.1)
unde:
![]() = autocorelatia reziduurilor de lag k .
= autocorelatia reziduurilor de lag k .
Determinarea nivelului lui Q permite verificarea modelului considerandu-se ca pentru un model stochastic, corect specificat, indicatorul Q calculat urmeaza o repartitie χ2 cu k- p- q grade de libertate. Ca urmare, acceptam modelul daca:
Q < ![]()
In acelasi scop poate fi utilizat, de asemenea, testul Bartlett, caz in
care modelul este confirmat daca coeficientii ![]() , calculati pe baza valorilor estimate ale variabilei
reziduale
, calculati pe baza valorilor estimate ale variabilei
reziduale ![]() , se situeaza in intervalul:
, se situeaza in intervalul:
![]() (
(![]()
In situatiile in care se pune problema optiunii intre doua variante ale modelului stochastic, se recomanda un indicator - semnal simbolizat RMS ("Root Mean Squares") si definit astfel
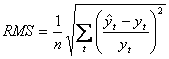 (6.2)
(6.2)
Alegem acea varianta de model stochastic pentru care indicatorul RMS prezinta valoarea cea mai apropiata de zero.
Estimarea parametrilor - etapa determinanta atat pentru modelele econometrice clasice cat si pentru analiza seriilor cronologice - reprezinta "o problema" si in cazul modelelor stochastice de prognoza. De modalitatea in care ea este rezolvata depinde nu numai calitatea prognozei, dar si raporturile care pot fi stabilite intre evolutia prezenta si viitoare si evolutiile din trecut.
Prin modelele de tip AR, MA, ARMA, ARIMA se urmareste
obtinerea de previziuni cat mai precise, ceea ce, in termenii statisticii,
inseamna ca, in urma compararii valorilor prognozate ![]() cu valorile reale
cu valorile reale ![]() ,eroarea medie patratica este minima:
,eroarea medie patratica este minima:
![]() (7.1)
(7.1)
Valoarea previzionata trebuie considerata mai curand o
speranta matematica a nivelului viitor al lui ![]() decat o marime certa
care s-ar obtine in conditii normale in viitor. Totodata un nivel previzionat
decat o marime certa
care s-ar obtine in conditii normale in viitor. Totodata un nivel previzionat ![]() reprezinta o marime
conditionata de valorile empirice obtinute pentru perioadele care preced
intervalul de prognoza:
reprezinta o marime
conditionata de valorile empirice obtinute pentru perioadele care preced
intervalul de prognoza:
![]() (7.2)
(7.2)
Corespunzator relatiei (7.2), rezulta ca prognoza se obtine "pas cu pas", fiecare nivel previzionat presupunand calcule prealabile care includ prognoza/prognozele din trecut. Astfel, daca seria cronologica prezinta valori pentru t = 1, 2, ., n, atunci previziunea pentru perioada n + 1 rezulta astfel:
![]()
![]()
![]() (7.4)
(7.4)
In relatia (7.4) nivelul
perturbatiei ![]() se determina in
prealabil pe baza relatiei (5.4)
fiind, de fapt, rezultatul diferentelor
se determina in
prealabil pe baza relatiei (5.4)
fiind, de fapt, rezultatul diferentelor ![]()
In general, un proces ARMA(p, q): ![]()
![]() conduce la prognoze
conduce la prognoze ![]() de eroare patratica
minima. Astfel, situandu-ne in momentul n
, rezulta ca, pentru momentul viitor n
+ v obtinem:
de eroare patratica
minima. Astfel, situandu-ne in momentul n
, rezulta ca, pentru momentul viitor n
+ v obtinem:
![]()
![]() (7.5)
(7.5)
Recomandari:
-
pentru valorile necunoscute ![]() (de exemplu,
(de exemplu, ![]() pentru a obtine
valoarea prognozata pentru
pentru a obtine
valoarea prognozata pentru ![]() ) utilizam valorile prognozate
) utilizam valorile prognozate ![]()
-
valorile variabilei reziduale ![]() (
(![]() ) utilizate pentru a obtine prognoze sunt cele ajustate,
) utilizate pentru a obtine prognoze sunt cele ajustate, ![]() , dar, pentru
, dar, pentru ![]()
![]() se considera ca
acestea sunt egale cu zero, fiind tratate ca rezultand dintr-un proces de
zgomot alb.
se considera ca
acestea sunt egale cu zero, fiind tratate ca rezultand dintr-un proces de
zgomot alb.
In cazul seriilor nestationare este necesar ca previziunile finale sa includa si componenta tendinta. Ca urmare, este necesar sa se procedeze, ori de cate ori tendinta a fost eliminata prin calculul diferentelor de diferite ordine, la efectuarea unui calcul invers celui care a dus la eliminarea trendului. Deci o insumare a fiecarui rezultat obtinut ca o prognoza "stationarizata" cu nivelul anterior obtinut in conditiile mentinerii tendintei.
Concret, in cazul in care modelul este de tip ARIMA(1,1,1), prognoza nivelului stationarizat pentru perioada n + 1 rezulta astfel:
![]() (7.6)
(7.6)
unde:
![]() = estimatii ale
parametrilor.
= estimatii ale
parametrilor.
![]() (7.7)
(7.7)
Pentru perioada n+2 prognoza stationarizata rezulta astfel:
![]()
intrucat:![]()
Rezulta ca:
![]() (7.8)
(7.8)
Pentru n+3 prognoza este:
![]() (7.9)
(7.9)
Seria
fiind nestationara de ordinul intai (d=1)
rezulta ca fiecare nivel obtinut constituie, de fapt, o diferenta de tip ![]() . Rezulta ca obtinerea
valorii
. Rezulta ca obtinerea
valorii ![]() care sa includa
tendinta presupune insumarea diferentei
care sa includa
tendinta presupune insumarea diferentei ![]() cu nivelul anterior
cu nivelul anterior ![]() . Pentru previziunile care, evident, depasesc perioada n, este necesar nivelul empiric, care
include trendul,
. Pentru previziunile care, evident, depasesc perioada n, este necesar nivelul empiric, care
include trendul, ![]() , astfel incat, adaugand acestuia valorile stationarizate ale
prognozei, sa putem obtine previziuni care includ tendinta[11].
, astfel incat, adaugand acestuia valorile stationarizate ale
prognozei, sa putem obtine previziuni care includ tendinta[11].
1)
Pentru datele prezentate in tabelul 5.1 exemplificam modalitatea de elaborare a
prognozelor. In acest caz modelul ARIMA(1,1,1)
a fost confirmat ca valid in urma etapei de verificare. Reamintim ca ![]()
![]() . Consideram, de asemenea,
. Consideram, de asemenea, ![]()
![]()
![]()
![]() , intrucat include media.
, intrucat include media.
Previziunile pentru urmatoarele perioade rezulta astfel:
pentru ![]()
![]() Þ
Þ ![]()
Includem
tendinta, insumand anterioarei valori ![]() (vezi tabelul 5.1 -
randul 1) prognoza obtinuta:
(vezi tabelul 5.1 -
randul 1) prognoza obtinuta:
y12*
-
pentru t = n + 2 = 11 + 2 = 13 avem in vedere faptul ca v>p, v>q,
in sensul ca "v" a devenit 2, iar
ordinul lui p si q este 1. Ca urmare, ![]()
Rezulta ca:
![]()
Includem
tendinta, insumand anterioarei valori (![]() ) ultimul rezultat prognozat
) ultimul rezultat prognozat ![]() in vederea obtinerii
prognozei
in vederea obtinerii
prognozei ![]()
y13*
![]()
![]()
![]()
De mentionat ca prognozele tind sa se stabilizeze in jurul unui anumit nivel (in cazul exemplificat acest nivel este 24). Asadar, modificarile in timp, dupa ce depasim prima, eventual a doua si a treia perioada de prognoza, devin tot mai putin "prognozabile". Pe termen lung, previziunile bazate pe modele care includ factori (vezi Capitolele III si IV) sunt mai credibile.
2) In tabelul 7.1 sunt redate previziunile privind productia de otel precum si vanzarile de aparate de radio in Romania. Modelele utilizate sunt:
pentru productia de otel
![]()
- evolutia vanzarilor de aparate de radio
![]()
Tabel 7.1
|
Perioada de prognoza |
Productia de otel (mii t) |
Vanzari de radioreceptoare (mii buc.) |
||
|
Previziuni |
Date reale |
Previziuni |
Date reale |
|
|
n n n n |
|
|
|
|
Calitatea modelului din punct de vedere al preciziei prognozelor poate fi verificata pe baza unor prognoze "de proba" avandu-se in vedere urmatoarele etape:
a) etapa specificarii, ca si cea a estimarii, se refera la seria de date pentru intervalul considerat, mai putin ultimele 5-6 perioade. Acest interval reprezinta "secventa martor";
b) pe baza modelului ales, sau a doua, trei variante de model, sunt obtinute previziuni
privind evolutia in cele 5-6 perioade care formeaza secventa martor;
c) se procedeaza la compararea prognozelor elaborate pentru fiecare
varianta de model cu datele reale care compun secventa martor. In acest fel,
putem aprecia care varianta este mai performanta. Indicatorul pe care l-am
simbolizat cu RMS (relatia (6.2))
poate fi util si pentru aceasta verificare si, pe baza lui, vom accepta acea
varianta de model pentru care am obtinut cea mai mica valoare a respectivului
indicator. Desigur, in relatia (6.2 ) nivelul
ajustat, ![]() , este inlocuit cu valoarea sa prognozata
, este inlocuit cu valoarea sa prognozata ![]() (t = n+1, n+2.). Varianta de model considerata
drept cea mai buna in urma unei astfel de verificari urmeaza sa fie utilizata
pentru intreaga serie
(t = n+1, n+2.). Varianta de model considerata
drept cea mai buna in urma unei astfel de verificari urmeaza sa fie utilizata
pentru intreaga serie![]()
"Familia" modelelor stochastice de prognoza continua sa se diversifice luand in atentie noi manifestari din economie cum sunt cele legate de sezonalitate (SARIMA), inconstanta in timp a dispersiei valorilor reziduale (ARCH), fractionarea decalajului in timp din modelele ARIMA (ARFIMA). In cele ce urmeaza ne vom referi la aceste din urma modele.
MODELUL ARCH (Autoregressive Conditional Heteroscedasticity) urmareste includerea manifestarii repetabile, observata in seriile cronologice privind indicatorii financiari - monetari (rata inflatiei, cursul de schimb, pretul activelor, preturile speculative), care consta in aparitia de erori de prognoza relativ mari in unele secvente de timp, in alternanta cu secvente in care erorile sunt mici. Este vorba deci de o inegala imprastiere (heteroscedasticitate) a valorilor variabilei reziduale manifestata pe secventele de timp care compun seria cronologica. Succesiunea de erori de prognoza mari, urmata de succesiunea de erori mult mai mici, poate fi intalnita atat in situatiile in care apreciem precizia previziunilor, cat si in situatiile in care analizam comportamentul valorilor variabilei reziduale pentru seria initiala de date. O dependenta manifestata sub forma autocorelatiei poate fi, deci, invocata. Econometricianul englez F. R. Engle a urmarit includerea in modelul stochastic de prognoza a unui astfel de comportament al valorilor reziduale, considerand ca dispersia erorii poate fi privita ca fiind dependenta de valorile lui yt-i sau ut-i inregistrate in trecut. In acest sens, este propusa functia
![]()
ca si varianta:
![]()
Spre
deosebire de modelul AR, in care eroarea, u, este considerata aleatoare, normal
distribuita, de medie egala cu zero si de dispersie ![]() , iar media conditionata a valorilor lui yt este dependenta de timp, M(yt/yt-1) =
a yt-1 , in versiunea propusa de Engle si dispersia erorii este
dependenta de timp, pierzandu-si calitatea de a fi
, iar media conditionata a valorilor lui yt este dependenta de timp, M(yt/yt-1) =
a yt-1 , in versiunea propusa de Engle si dispersia erorii este
dependenta de timp, pierzandu-si calitatea de a fi
![]()
O varianta simpla a modelului poate fi redata astfel:
![]() (7.13)
(7.13)
![]() (7.14)
(7.14)
![]()
Intre variantele modelului ARCH mentionam expresia generalizata propusa de Bollerslev (GARCH), in care "memoria" procesului este raspandita pe mai multe date observate pentru trecut
![]()
Restrangand efectul intarzierii la o singura unitate de timp t - 1, obtinem modelul GARCH(1,1):
![]() (7.16)
(7.16)
unde:
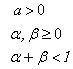
Mentionam de asemenea, varianta integrata, IGARCH, in
care valorile lui yt devin
stationare dupa calculul diferentelor de ordinul intai
varianta in care efectul dependentei dispersiei, ![]() , in raport cu timpul apare la nivelul valorilor medii ale
procesului, ARCH-M varianta exponentiala, E GARCH, in care dispersiei
conditionate de
valorile lui
, in raport cu timpul apare la nivelul valorilor medii ale
procesului, ARCH-M varianta exponentiala, E GARCH, in care dispersiei
conditionate de
valorile lui ![]() sau
sau ![]() din trecut ii este
impusa restrictia de a fi nenegativa prin considerarea logaritmilor valorilor
lui
din trecut ii este
impusa restrictia de a fi nenegativa prin considerarea logaritmilor valorilor
lui ![]() ca fiind dependente de
valorile reziduale din trecut [7].
ca fiind dependente de
valorile reziduale din trecut [7].
Daca abordam modelul ARCH sub aspect operational precum
si prin prisma utilitatii sale in analiza si prognoza, mentionam, in primul
rand, criteriile care confirma sau infirma optiunea pentru un astfel de model.
Ele constau in verificarea semnificatiei parametrilor din ecuatia (7.11) :![]() (pentru
(pentru ![]() optiunea pentru ARCH
este infirmata), sau in aplicarea testului F, caz in care, pentru
optiunea pentru ARCH
este infirmata), sau in aplicarea testului F, caz in care, pentru ![]() χ2 (p
= numarul de termeni), optiunea pentru ARCH este confirmata.
χ2 (p
= numarul de termeni), optiunea pentru ARCH este confirmata.
Estimarea parametrilor poate fi realizata iterativ
incepand cu aplicarea M.C.M.M.P. modelului "de baza" (vezi relatia (7.13)). Se continua cu obtinerea de
valori ajustate, ![]() , determinarea valorilor variabilei reziduale si a dispersiei
acesteia,
, determinarea valorilor variabilei reziduale si a dispersiei
acesteia, ![]() . In etapa urmatoare, cunoscand
. In etapa urmatoare, cunoscand ![]() , se poate proceda la estimarea parametrilor
, se poate proceda la estimarea parametrilor ![]() din relatia (7.14) si, in cazul in care
din relatia (7.14) si, in cazul in care ![]() difera semnificativ de
zero, heteroscedascitatea este confirmata. Ca urmare, varianta ponderata a
M.C.M.M.P. este recomandata. Ea consta in impartirea valorilor
difera semnificativ de
zero, heteroscedascitatea este confirmata. Ca urmare, varianta ponderata a
M.C.M.M.P. este recomandata. Ea consta in impartirea valorilor ![]() la
la ![]() si reluarea aplicarii
M.C.M.M.P. pentru obtinerea valorilor ajustate,
si reluarea aplicarii
M.C.M.M.P. pentru obtinerea valorilor ajustate, ![]() ("imbunatatite"), urmata de determinarea noilor erori,
("imbunatatite"), urmata de determinarea noilor erori, ![]() , a dispersiei acestora si de estimarea parametrilor din
ecuatia (7.14). Reluarea procesului
are loc pana cand parametrul
, a dispersiei acestora si de estimarea parametrilor din
ecuatia (7.14). Reluarea procesului
are loc pana cand parametrul ![]() devine nesemnificativ
in sensul testului t.
devine nesemnificativ
in sensul testului t.
Intre avantajele abordarii modelarii prin prisma ARCH
mentionam perspectiva oarecum diferita in care este pusa problema autocorelarii
variabilei reziduale. In cazul in care existenta autocorelarii este confirmata
prin testul D-W, aceasta s-ar putea datora, fie faptului ca ![]() depinde de
depinde de ![]() , fie faptului ca dispersia valorilor variabilei reziduale,
calculata pe segmente ale sirului de valori,
, fie faptului ca dispersia valorilor variabilei reziduale,
calculata pe segmente ale sirului de valori, ![]() , este dependenta de trecut. S-ar putea afirma, in aceasta
din urma situatie, ca autocorelarea semnalata de testul D-W este, de fapt,
heteroscedascitate. In ceea ce priveste modelul ARCH si prognoza, mentionam ca
predictiile se bazeaza pe o informatie suplimentara prin luarea in calcul a
inconstantei in timp a dispersiei valorilor reziduale, ceea ce, cel putin sub
aspect teoretic, creeaza premise pentru obtinerea de prognoze mai precise.
, este dependenta de trecut. S-ar putea afirma, in aceasta
din urma situatie, ca autocorelarea semnalata de testul D-W este, de fapt,
heteroscedascitate. In ceea ce priveste modelul ARCH si prognoza, mentionam ca
predictiile se bazeaza pe o informatie suplimentara prin luarea in calcul a
inconstantei in timp a dispersiei valorilor reziduale, ceea ce, cel putin sub
aspect teoretic, creeaza premise pentru obtinerea de prognoze mai precise.
MODELUL ARFIMA
("Autoregressive Fractionally Integrated Moving Average") reprezinta o
varianta a modelului ARIMA(p,d,q), in care coeficientul "d", care semnaleaza ordinul diferentei,
reprezinta o fractiune din unu. Asadar, o fractiune a decalajului in timp 0<d<1 este suficienta pentru a
stationariza seria. Se poate afirma ca modelul ARIMA pentru care d=1, (![]() ) sau d=2 (
) sau d=2 (![]() ) etc., "d"
reprezentand doar valori intregi, devine un caz particular al clasei mai largi
de modele ARFIMA.
) etc., "d"
reprezentand doar valori intregi, devine un caz particular al clasei mai largi
de modele ARFIMA.
Din perspectiva economiei, acceptarea ordinului de integrare reprezentat de o fractiune din unu se justifica daca avem in vedere componentele inertiale "subterane" care se manifesta ca o tendinta de perioada indelungata, avand inceputul dincolo de primul termen al seriei pe care o analizam si pentru care diferentele de ordinul intai ar fi prea mari [3]. Astfel de procese precum: nivelarea consumului, rasplata investitiilor in actiuni, punerea de acord a salariilor cu preturile, formarea traditiilor in consum dar si in productie sau investitii, ar fi indicate pentru o abordare in sensul modelelor ARFIMA. Procesele de acest gen necesita "modele de memorie foarte lunga", capabile sa retina aspecte legate de persistenta unor factori in economie cum ar fi: acumularile de capital fie uman, fie de natura tehnologica, traditiile, tendinta de "mai bine" etc. Modelele bazate pe conceptul de radacina unitara (vezi Capitolul VI), dar si mai recentul model ARFIMA sunt destinate descrierii unor astfel de procese de persistenta.
Exprimarea formala a modelului se poate baza pe expresia "fractionata" a perturbatiei pentru variabila timp, considerata de tip discret:
![]() (7.17) unde:
(7.17) unde:
d = numar
real ![]()
B = operator de "trimitere" in trecut (vezi tabelul 2.1).
Daca consideram dezvoltarea binomiala a elementului ![]() , aceasta devine:
, aceasta devine:
![]() (7.18)
(7.18)
Daca se adauga si componentele AR si MA expresiei mentionate, se ajunge la modelul ARFIMA, a carui forma generala poate fi exprimata astfel:
![]() (7.19)
(7.19)
![]()
unde a, b si B au aceeasi semnificatie ca si in relatia (5.4).
Estimarea, in principiu, presupune, intr-o prima faza, determinarea marimii fractiunii "d", dupa care se trece la estimarea parametrilor modelului ARMA la care s-a ajuns.
Incheiem prezentarea generala a modelului ARFIMA mentionand ca acest model a intrat in atentia economistilor doar in ultimul timp, oferind un domeniu de cercetare si aplicare prea putin exploatat.
BIBLIOGRAFIE
Box, G., E., P., Jenkins,
G., M., - Time Series Analysis,
Forecasting and Control, HoldenDay,
Cuthbertson, K., Hall, S., - Applied Econometrics Techniques, Whreatons Ltd., 1995
Fomby, T., B., Rhodes, G.,.
- Advances in Econometrics, JAI
Gress,
Granger, C., W., J., - Spectral Analysis of Economic Time Series,
Gujarati, D., - Basic Econometrics, McGraw-Hill Inc., N. Y., 1995
Harvey, A., C., - Time Series Models, Howester, N. Y.,1993
Maddala, G., S., - Introduction to Econometrics, McMillan Publ., 1988
Pecican, E., S., - Econometrie, Editura All, Bucuresti,1994
Ploeg, F.(edit) - Advanced Lectures in Quantitative Econometrics, Acad. Press, 1990
Stewart, J., - Econometrics, Allan Th., 1991
Tertisco, M., Stoica, P., Popescu, Th.., - Modelarea si predictia seriilor de timp, Editura Academiei, Bucuresti, 1985
Expresia zgomot alb este utilizata pentru a caracteriza procesele pur aleatoare in care nici o componenta (de frecventa) nu prezinta o mai mare importanta decat altele. Starea de "deplina egalitate" face ca procesul sa prezinte analogii cu acea unda de lumina in care nu predomina nici o componenta pentru a-i da culoarea, ea ramanand alba. Mai concret, daca M(u) = 0, su = finita, valorile lui ut nu sunt autocorelate, afirmam ca procesul generator de valori ut este de zgomot alb, iar daca, in plus, erorile ut sunt independente, afirmam ca procesul este strict de zgomot alb.
Prin indicele k (k = 1, 2, 3 .) consemnam intarzierea dupa care se "simte" influenta (lagul) erorii din trecut.
Relatia de calcul (1.2) nu difera semnificativ de modul de calcul al coeficientului
de corelatie. Deosebirea consta in faptul ca, in loc de "x" apare yt-k.
Intrucat in cazul proceselor stationare ![]() , numitorul devine:
, numitorul devine:
![]() (numarul gradelor de libertate se simplifica).
(numarul gradelor de libertate se simplifica).
Denumirea de medie mobila are in vedere
faptul ca suma algebrica a elementelor ![]() (k = 1, 2, ., q)
reprezinta numaratorul unei medii ponderate ipotetice, ponderile fiind
(k = 1, 2, ., q)
reprezinta numaratorul unei medii ponderate ipotetice, ponderile fiind ![]() , ai carei
termeni gliseaza pe masura ce "t"
creste. Ulterior, conditia
, ai carei
termeni gliseaza pe masura ce "t"
creste. Ulterior, conditia ![]() a fost "uitata",
astfel incat modelul
a fost "uitata",
astfel incat modelul ![]() reprezinta un agregat
de q elemente cu rol semnificativ in
evolutia variabilei y.
reprezinta un agregat
de q elemente cu rol semnificativ in
evolutia variabilei y.
Semnul negativ al parametrului b este pur simbolic. Parametrul va avea semnul rezultat in urma estimarii.
In unele lucrari este utilizat termenul "identificare" in sensul atribuit de noi specificarii. Intrucat identificarea apare intr-un capitol urmator ca etapa distincta in modelarea econometrica, preferam sa utilizam notiunea de specificare a variabilelor, a functiei sau de elaborare a modelului.
Explicatia acestei reguli are in vedere
faptul ca, intrucat ![]() pentru
pentru ![]() rezulta ca, pentru
expresiile valorilor lui
rezulta ca, pentru
expresiile valorilor lui ![]() si
si ![]() se obtine
se obtine ![]() ceea ce aminteste de
ceea ce aminteste de ![]() Deci,
Deci, ![]() , pentru
, pentru ![]() si
si ![]() , pentru
, pentru ![]() . Intrucat coeficientul de autocorelatie
. Intrucat coeficientul de autocorelatie ![]() , rezulta ca si coeficientii de autocorelatie
, rezulta ca si coeficientii de autocorelatie ![]() sunt egali cu zero
pentru
sunt egali cu zero
pentru ![]() .
.
Modul in care s-a ajuns la aceste relatii este aratat in paragraful anterior (vezi relatiile (3.23) - (3.29).
Reamintim in modelul MA sau ARMA semnul
minus din fata parametrului b este
pur simbolic. In calcule avem in vedere rezultatele estimarii. In exemplul
considerat: ![]()
In ce priveste
intervalul de prognoza avem in vedere limitele stabilite pe baza relatiei: ![]() , in care:
, in care: 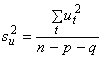
![]() = ponderi reprezentate
de parametrii estimati pentru varianta transformata a modelului ARMA in model
MA de ordin infinit (vezi paragraful care se refera la reductibilitatea
procesului AR la un proces MA).
= ponderi reprezentate
de parametrii estimati pentru varianta transformata a modelului ARMA in model
MA de ordin infinit (vezi paragraful care se refera la reductibilitatea
procesului AR la un proces MA).