Generatorul Van de Graaff,Acceleratorul liniar,Ciclotronul - Accelerator de particule

Acceleratoare de particule

Realizarea si studiul reactiilor nucleare nu pot fi facute decat daca particula-proiectil va primi o energie cinetica suficienta pentru a initia reactia. Ca urmare, se construiesc acceleratoare de particule capabile sa furnizeze energia necesara. Pot fi accelerate in mod direct doar particule cu sarcina, in acest scop utilizandu-se diverse combinatii de campuri electrice si magnetice, statice sau variabile, omogene sau neomogene. Dezvoltarea acceleratoarelor incepe dupa 1962, ca urmare directa a descoperirii reactiilor nucleare. In tab.1 sunt cuprinse principalele date privind acceleratoarele de particule.

Primul tip de accelerator este cel electrostatic sau direct. El se compune dintr-un generator de inalta tensiune (continua), o sursa de particule, un tub de accelerare si o tinta. Aceste parti componente pot fi gasite, cu mici modificari, la toate tipurile de acceleratoare. Generatorul de inalta tensiune, poate fi o masina electrostatica, un transformator ridicator de tensiune urmat de un grup de redresori, sau instalatii special construite, cum ar fi generatorul Van de Graaff sau generatorul de cascada, de tipul Cocroft-Walton. Tensiunea inalta pe care o furnizeaza generatorul se aplica unor electrozi ce formeaza un condensator. Unul dintre electrozi contine sursa de particule, iar pe celalalt se pune tinta formata din nucleele pe care dorim sa le bombardam. In cursul acelerarii particulele trec printr-un tub vidat, numit tub de accelerare. Tubul este astfel construit, incat particulele sa formeze un fascicul convergent pe tinta. Daca tensiunea inalta aplicata este V, atunci energia pe care o va castiga o particula in acceleratorul direct va fi E=qV, unde q este sarcina electrica pe care o poseda particula. Se vede ca pentru aceeasi tensiune de accelerare, energia particulei este cu atat mai mare, cu cat sarcina q este mai mare. Ca atare, accelerarea directa este convenabila mai ales pentru particulele grele, cu sarcina mare (ioni multiplu ionizati). Intensitatea fasciculului de particule aceelerat se masoara de obicei prin curentul electric corespunzator. Spre exemplu, un curent de protoni de 1 mA corespunde unui flux de 6*10¹⁶ particule pe secunda.  

a) Generatorul Van de Graaff este o masina electrostatica prin influenta, care permite producerea a milioane de volti. In fig 1 se poate vedea schema unui astfel de generator. El este format dintr-o sfera metalica, goala in interior, de raza R, ce formeaza o cusca Faraday si care prin intermediul colectorului (B) culege sarcinile de pe banda transportoare (C). Banda transportoare primeste, la randul ei, sarcina de la un generator obisnuit, de inalta tensiune (10 - 20 kV), prin intermediul unor varfuri ascutite (a). Pentru realizarea transportului, banda se confectioneaza din cauciuc sau un alt material izolant si este pusa in miscare de catre un motor electric, in sensul indicat in figura, cu viteza constanta v. Sursa de inalta tensiune se aplica (borna pozitiva) unui sistem de varfuri ascutite, plasate in fata benzii transportoare, care, pe partea cealalta, are un electrod la borna negativa. In jurul varfurilor se produce un fenomen de ionizare intens, datorita campului electric foarte mare ce exista in preajma lor. Ca urmare, pe banda transportoare se vor proiecta ionii pozitivi respinsi de varfurile ascutite (efect Corona), fiind astfel antrenate cu viteza uniforma v, si dusa in interiorul sferei. Ajungand in punctul B din interior, sarcina va fi colectata de catre sfera, prin intermediul sistemelor de perii legate electric de ea. Datorita efectului de cusca Faraday, sarcina se va raspandi pe suprafata sferei, de unde nu mai poate reveni. Sfera, avand o capacitate C (=4 pe R fata de Pamant), pe masura ce se va incarca cu sarcina electrica, isi va ridica tensiunea conform relatiei U=Q/C. Limita superioara pe care poate sa o atinga tensiunea este data pe deoparte de raza sferei, pe de alta parte de rigiditatea dielectrica a mediului in care este plasata sfera (limita de strapungere prin scanteie a mediului dielectric). Pentru aer, valoarea maxima a campului electric, in conditii normale, este de E_d=30kV/cm. Deoarece intensitatea campului la suprafata sferei va fi E=U/R , valoarea maxima a tensiunii ce poate fi atinsa este:

U_max =R*E_d

se vede ca tensiunea maxima creste cu cresterea razei sferei.

Pentru a mari tensiunea acceleratoare, se poate cupla doua generatoare Van de Graaff, incarcate cu sarcini opuse, dublandu-se astfel tensiunea. Acest ansamblu se numeste tandem. Un generator Van de Graaff cu raza sferei de 1 m, cu o banda de 50 cm latime, antrenata cu o viteza de 20 m/s va produce o tensiune maxima (teoretica) de 3 MV si un curent maxim de 0,5 mA.

b) Acceleratorul liniar face parte din grupul de acceleratori de rezonanta sau ciclici, deoarece accelerarea se face prin trecerea repetata a particulelor printr-o zona acceleratoare. Existenta unui astfel de ciclu va cere, dupa cum se va vedea, respectarea unei conditii de sincronism. Acceleratorul liniar este construit (fig 2) dintr-o incinta vidata, in care este plasata o sursa de ioni si o serie de cilindri metalici (tuburi de fuga), asezati unul dupa altul, centrati si de lungime crescanda. La capatul lor se aseaza tinta ce va fi bombardata. Alimentarea tuburilor se face de la o sursa de inalta frecventa si inalta tensiune. Accelerarea se petrece in zona dintre tuburi, iar in interiorul tuburilor particulele se misca liber (inertial). Conditia de sincronism (de rezonante sau de ciclitate) se pune astfel: pentru a fi accelerata, particula trebuie sa gaseasca la iesirea din tub un potential accelerator (tubul sa aiba o polaritate inversa semnului sarcinii acceleratoare). Cum viteza va creste la fiecare treapta de accelerare, rezulta ca lungimea acestor tuburi va trebui sa creasca in mod proportional, deoarece frecventa tensiunii aplicate este constanta (f). Daca tensiunea generatorului este U₀ , la fiecare regiune de accelerare, energia particulei va creste cu qU₀ , iar daca n este numarul de astfel de tuburi, energia totala va fi:

E=n*q*U₀

q fiind sarcina particulei accelerate. La prima accelerare particula isi va creste energia de la zero la qU₀ . In mod corespunzator, viteza particulei va fi data de legea de conservare a energiei care, in limita neralitivista (E< mc)² , este

v₁=

In intervalul de timp T/2=1/(2*f) particula va trebui sa se miste in interiorul tubului, timp in care se va petrece schimbarea polaritatii tubului astfel ca la iesirea din primul tub sa-l gaseasca pe cel de-al doilea cu o polaritate convenabila pentru accelerare. De aici rezulta:

l₁=v₁*=

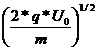
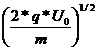
In urmatoarea zona accelerare, particula isi va creste energia de la q*U₀ la 2*q*U₀ , iar viteza ei va deveni:

;

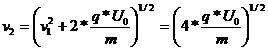
Generalizand aceasta relatie, vedem ca la iesirea din cel de-al n-lea tub, particula va avea viteza 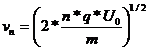, de unde relatia ce ne da lungimea celui de al n-lea tub,

l_n=

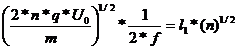
In acest fel se vede ca lungimea tuburilor creste cu (n)^1/2 din care cauza obtinerea energiilor mari necesita lungimi de kilometri. Relatia dintre parametrii geometrici (constructivi) ai acceleratorului si frecventa tensiunii de alimentare. Pentru o energie data, lungimea tuburilor scade cu cresterea frecventei tensiunii de accelerare, motiv pentru care ele se alimenteaza cu tensiuni ce au frecvente de ordinul a 1000 -10000 MHz.

Daca particula accelerata este electronul, atunci ea devine repede relativista si conditia de sincronism nu mai este indeplinita. Variatia masei cu viteza arata ca un electron de 1 MeV (cu viteza de v=0.93*c) are o masa de aproape patru ori mai mare ca masa de repaus.

c) Ciclotronul este tot un accelerator ciclic, de rezonanta in care particulele nu se misca rectiliniu, ci circular, folosindu-se in acest scop campuri magnetice omogene. Ca urmare, dimensiunea ciclotronului este mult mai mica ca a unui accelerator liniar. In centrul sistemului si in camp magnetic se gaseste o sursa de particule. Tot in acest camp se gasesc si doi electrozi de o forma speciala, numiti duanti (au forma asemanatoare literei D). Particulele sunt accelerate la trecerea intre duanti, iar in interiorul lor se misca liber, ca si in tuburile de fuga ale acceleratorului liniar. Conditia de sincronism va cere ca intotdeauna la iesirea din duant, particula sa aiba in fata polaritatea acceleratoare. Miscarea unei particule de masa m, sarcina q si viteza v, intr-un camp de intensitate B, se va face pe o traiectorie circulara de raza r, perioada T si pulsatia w dete de relatiile

r = m*v/(q*B) T=2*p*m/(q*B) w = q*B/m

Deoarece perioada de rotatie nu depinde de energia particulei (in limite neralitiviste), conditia de sincronism va fi data de f=2/T, f fiind frecventa tensiunii alternative, aplicata pe duanti. Traiectoria particulei va fi o succesiune de semicercuri cu raze treptat crescatoare. In momentul in care particula atinge raza maxima de rotatie, un electrod special asigura scoaterea ei de pe traiectorie si din ciclotron si o indreapta catre tinta. Energia maxima va fi data de raza maxima R,

E_c = p²/(2*m) = (q*B*R)²/(2*m),

Energia maxima atinsa in mod obisnuit este de 20-30 MeV.

Conditia de sincronism contine masa particulei; deci, pentru particule ce devin rapid relativiste, ciclotronul nu va fi un accelerator potrivit. Ca atare, el va fi bun pentru accelerarea particulelor grele (particule alfa, protoni, deutroni ioni grei) dar nu si pentru electroni.0

Pentru a accelera electroni, va trebui sa variem fie frecventa, fie campul magnetic, fie ambele, pe masura ce particula isi creste energia. Corespunzator celor trei situatii, vor exista trei tipuri de acceleratori:

sincrotronul , la care campul magnetic variaza, astfel incat raportul m*v/B sa fie constant;

sincrociclotronul (fazotronul), la care frecventa variaza, astfel incat produsul m*v*f sa fie constant;

sincrotronul de protoni (sincrofazotronul), la care se produce atat variatia frecventei, cat si variatia campului magnetic, astfel incat m*f/B sa fie constant. 

Malaescu Marius-Claudiu

clasa a XII a G