1. DETERMINANTI

2.1. Definitia determinantului de ordin n4

Fie A= o matrice patratica. Vom asocia acestei matrici un numar notat det(A) numit determinantul matricii A.

Definitie. Daca A= este o matrice patratica de ordinul intai, atunci

det(A) =.

Definitie. Determinantul matricii 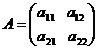este numarul

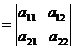
si se numeste determinant de ordin 2. Termenii , se numesc termenii dezvoltarii determinantului de ordin 2.

Definitie. Determinantul matricii

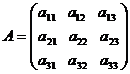este numarul

si se numeste determinant de ordin 3. Termenii care apar in formula se numesc termenii dezvoltarii determinantului.

Pentru calculul determinantului de ordin trei se utilizeaza trei tehnici simple:

Regula lui Sarrus

Fie determinantul de ordin 3, Pentru a calcula un astfel de determinant se utilizeaza tabelul de mai jos.

(am scris sub determinant

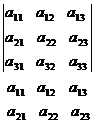
primele doua linii)

Se face produsul elementelor de pe diagonale. Produsul elementelor de pe o diagonala descendenta este cu semnul plus. Avem trei astfel de produse: .

Produsul elementelor de pe o diagonala ascendenta este cu semnul minus. Avem trei astfel de produse: .

Suma celor sase produse da valoarea determinantului d de ordin 3. Acest procedeu de calcul se numeste „regula lui Sarrus”.

Regula triunghiului

Am vazut ca determinantul de ordin trei are in dezvoltarea sa sase termeni, trei cu semnul plus si alti trei cu semnul minus.

Primul termen cu plus se gaseste inmultind elementele de pe diagonala principala, iar ceilalti doi, inmultind elementele situate in varfurile celor doua triunghiuri care au o latura paralela cu cu diagonala principala. Dupa aceeasi regula, referitoare la diagonala secundara, se obtin termenii cu minus.

Obs.: Atat „regula lui Sarrus” cat si „regula triunghiului” se aplica numai determinantilor de ordin 3.

Exemplu. Sa se calculeze prin cele doua metode de mai sus determinantul

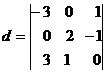
R. Regula lui Sarrus.

Regula triunghiului

Recurent (sau dezvoltare dupa o linie sau o coloana)

Determinantul de ordin 3 are 6 ( = 3!) termeni dintre care trei sunt cu semnul plus, iar ceilalti cu semnul minus.

Are loc urmatoarea proprietate:

, (1)

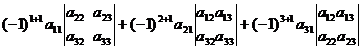= . (2)

Observatii

1) Egalitatea (1) se mai numeste dezvoltarea determinantului dupa elementele liniei intai, iar egalitatea (2) se numeste dezvoltarea determinantului dupa elementele coloanei intai.

2) Formulele (1) si (2) sunt relatii de recurenta, deoarece determinantul de ordin 3 se exprima cu ajutorul unor deteminanti de ordin inferior (2).

2.2. Definitia determinantului de ordin n

Voi defini in continuare determinantul de ordin n prin recurenta cu ajutorul determinantilor de ordin n – 1. Pentru aceasta sunt necesare unele precizari.

Fie A=.

Definitie1. Se numeste minor asociat elementului determinantul matricii patratice de ordin n – 1 obtinut prin suprimarea liniei i si coloanei j din matricea A. Se noteaza acest minor prin sau .

Definitie2. Se numeste complement algebric al elementului numarul . Exponentul al lui (–1) este suma dintre numarul liniei i si coloanei j pe care se afla .

Definitie. Determinantul matricii A=de ordin n este suma produselor elementelor din prima linie cu complementii lor algebrici adica

.

Observatii

1) Elementelor, liniilor si coloanelor matricii A le vom spune de asemenea elementele, liniile si coloanele determinantului

.

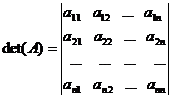2) Formula din definitie spunem ca reprezinta dezvoltarea determinantului de ordin n dupa elementele primei linii.

3) Definitia determinantului de mai sus este inca putin eficienta (o voi ilustra mai jos pentru n = 4). De aceea se impune stabilirea unor proprietati ale determinantilor care sa fie comode atat din punct de vedere al teoriei si din punct de vedere calculatoriu. Aceste proprietati le prezint in paragraful urmator.

4) Continuand cu explicitarea determinantilor de ordin n – 1 din definitie se obtine pentru o suma de produse de elemente din determinant, fiecare produs continand elemente situate pe linii si coloane diferite.

5) Determinantul este o functie .

Exemplu Sa se calculeze determinantul de ordin 4:

.

R. Aplicam definitia data mai sus pentru n = 4 si dezvoltam determinantul dupa elementele liniei intai. Avem:

=

=,

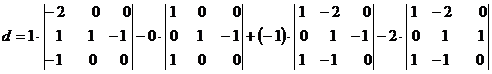unde determinantii de ordin 3 i-am calculat prin una din metodele prezentate la determinantii de ordin 3.