Rezolvarea ecuatiilor de gradul III si IV

Cardano s-a nascut intr-o localitate nu departe de Milano. Tatal sau era jurisconsult. Conform izvoarelor istorice el era un om luminat si de viata.Cunostea mai multe limbi straine, se ocupa de matematica, filosofie si traduceri.

Fazzio Cardano(acesta era numele tatalui lui Girolamo) s-a ocupat indeaproape de educatia fiului. Cardano a ales insa sa studieze medicina. In 1524,an in care moare Fazzio, Cardano primeste titlul de doctor in medicina al Universitatii din Padova. Se duce sa profeseze medicina la Milano.Acolo insa, Colegiul de Medicina al orasului ii refuza autorizatia de practica: motivul era acela ca Girolamo era in realitate fiul lui Fazzio. Evident, era vorba de un pretext, in fapt, colegii de breasla ai lui Cardano erau speriati probabil de acesta, datorita multiplelor sale cunostinte, personalitatii sale iesite din obisnuit.

In 1534,Cardano incearca din nou sa obtina o slujba la Milano,dar abia peste un an reuseste sa i se dea dreptul de practicare a medicinei in acest oras.

La Milano,Cardano are norocul sa vindece cateva personalitati de seama si astfel incepe ascensiunea sa si inceputurile unei vieti materiale mai bune, care-i permite sa se dedice exclusiv stiintei.

Astfel,in 1539,publica la Nurnberg (in limba latina) ,,Arimetica practica'',lucrare bine primita in Franta si Germania. In 1545 apare principala lucrare a lui Cardano in domeniul matematicii,intitulata ,,Ars magna sive de Regulis Algebraicis''(,,Marea arta sau despre regulile algebrice''),in care sunt incluse solutiile ecuatiilor generale de gradul III si IV,ultima problema fiind rezolvata de elevul sau Lodovico Ferrari.

Cardano mai calatoreste in Scotia ca medic al arhiepiscopului John Hamilton ,pe care reuseste sa-l vindece de o boala grea.

Trebuie mentionat ca in tot decursul vietii Cardano a fost preocupat de astrologie,ajungand datorita cunostintelor (de astronomie,de fapt) un fel de astrolog oficial al papei.Regele Frantei si regina Scotiei l-au luat si ei la randul lor sub protectie,ceea ce este o dovada ca gloria sa stiintifica de medic si astrolog practicant era destul de mare.

Astrologia ii va aduce totusi neplaceri lui Cardano. In 1554 scrie o carte intitulata ,,Asupra semnificatiei stelelor'' in care are proasta inspiratie sa includa un horoscop al lui Iisus Hristos (alcatuit de el insusi).

Inchizitia reuseste pe aceasta baza sa obtina in 1570 intemnitarea sa. La interventia unor prieteni supusi este eliberat peste doua luni ;mai ispaseste un ,,arest la domiciliu'' de trei luni si primeste recomandarea de a nu mai preda sau a mai scrie carti.

Cardano pleaca la Roma sa se puna direct sub protectia papei. In 1573,papa ii acorda o pensie suficienta pentru a se putea dedica activitatii stiintifice. In acesti ultimi ani ai vietii Cardano s-a scufundat printre manuscrisele sale.N-a mai predat,n-a mai publicat nimic,n-a mai practicat medicina. A lasat foarte multe lucrari nepublicate,printre care si o ,,Autobiografie'', extrem de interesanta prin modul in care Cardano surprinde caracteristici ale epocii respective.

In 1576, dupa unii biografi, Cardano s-a sinucis pentru a dovedi forta sa de astrolog prooroc,acesta fiind anul in care ar fi trebuit sa moara. Totusi, se pare ca Girolamo isi proorocise disparitia exact la 5 decembrie 1573-deci cu trei ani mai devreme.

Revenind la problema ecuatiei de gradul III, putem spune ca in realitate Cardano ,,n-a furat'' solutia lui Tartaglia, incluzand-o fara voia acestuia in Ars Magna.Practic el a descoperit la Bologna manuscrisul lui del Ferro,dar care ulterior pierzandu-se,s-a crezut ca Girolamo a mintit relativ la existenta acestuia.Aproape patru secole mai tarziu, profesorul italian Ettore Bortolotti a redescoperit manuscrisul lui del Ferro si astfel,specialistii au putut avea revelatia faptului ca ,,magicianul Cardano " a fost acuzat oarecum pe nedrept .

Cardano are insa meritul de a fi investigat ecuatia de gradul III mai profund decat Tartaglia.

Este poate util sa recapitulam-pe puncte-aceasta incalcita istorie:

1.-in jurul anului 1515,Scipione del Ferro, profesor la Universitatea din Bologna, da regula generala a rezolvarii ecuatiei:

2.-secretul nu este divulgat decat la doua persoane(una dintre ele:

Antonio Fior).

3.-in 1530 are loc un turnir matematic (initiat de Giovanni Colla) la care se propun spre rezolvare ecuatii particulare de tipul:

.

4.-participa la turnir Niccolo Tartaglia care rezolva problemele in timp record

5.-in 1535 Antonio Fior lanseaza si el un turnir, provocandu-l pe Tartaglia

-s-au propus ecuatii de tipul:

6.-Tartaglia rezolva din nou problemele si propune alte ecuatii pe care insa Fior nu este in stare sa le solutioneze

7.-apare Cardano:scria in acest timp ,,Ars Magna" si roaga pe Tartaglia sa-i divulge secretul formulei

-acesta refuza

-ulterior cedeaza,dar sub rezerva nepublicarii acesteia

8.-in 1539,impreuna cu Lodovico Ferrari,Cardano publica in ,,Ars Magna" solutia lui del Ferro-Tartaglia

9.-Cardano da in plus reducerea unei ecuatii cubice complete la o ecuatie cubica doar cu trei termeni

10.-socotit multa vreme ,,delapidator" al lui Tartaglia , Cardano este ,,reabilitat" prin redescoperirea,in 1923,a manuscrisului original al lui del Ferro

11.-in ,,Ars Magna" ,apare pentru prima oara solutia generala a ecuatiei de gradul IV ,solutie data de Ferrari

Ecuatia de gradul III, desi aparent simpla,ascunde in sine mare bogatie de idei matematice.

Sa intram putin in lumea ecuatiei de gradul III. In mod normal ar trebui sa incepem cu rezolvarea ei.

Fie deci:

Cu ajutorul transformarii , facem sa dispara termenul in

Ecuatia de gradul III se poate scrie in final :

Cea mai utilizata metoda de rezolvare a acestei ecuatii este cea data de matematicianul olandez J. Hudde (1628-1704), care, printre altele, a fost si primar al Amsterdamului.

Ideea lui a fost sa scrie radacina sub forma x=u+v si sa scrie apoi identitatea:

Se vede deci ca trebuie sa avem

sau de fapt:

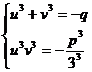
Alcatuim asadar ecuatia de gradul al doilea II cu radacinile:

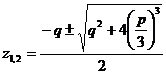
pe care le scriem astfel:

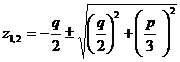
Obtinem imediat:

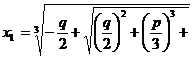
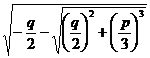
Celelalte doua radacini sunt si fiind radacinile cubice ale unitatii.

Ceea ce am scris mai sus poarta numele de FORMULA LUI CARDANO.

Expresia:

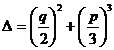
poarta numele de ,,discriminantul ecuatiei de gradul III " si ea joaca un rol important in stabilirea naturii radacinilor acestei ecuatii. Sa examinam pe rand situatiile posibile.

CAZUL D =0. Evident, cel mai simplu, dar instructiv. Atunci:

care se mai poate scrie:

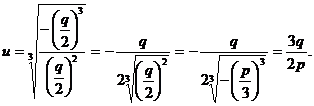
deoarece daca ,  atunci:

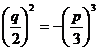
Din rezolvarea ecuatiei , stim ca :

      deci

adica:

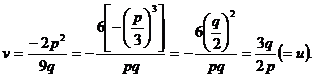
Prin urmare x₁ =u+u=2u=3q/p.

Sa facem urmatoarea observatie: daca este o radacina cubica a unitatii, adica atunci si deci:

Cum aici u=v,avem deci x₂ =-u si x₃ =-u ,adica

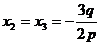
Iata deci ca in cazul D=0, radacinile ecuatiei pot fi scrise direct,si anume,

EXEMPLU (L.Ya. Okunev, 1951):ecuatia are radacinile x₁ =-4 si x₂=x₃ =2 . Intr-adevar :

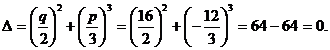
deci

2)CAZUL >0. De fapt ,ca si in cazul <0 exista trei radacini distincte.O demonstratie frumoasa este prin reducere la absurd. Presupunem ca radacinile nu ar fi distincte ,deci cel putin doua ar coincide: si

Atunci relatiile lui Viete dau:

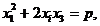
Avem deci:

.

Prin urmare:

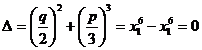
ceea ce contrazice ipoteza D0.

Precizarea in plus la cazul nostru (D>0) este aceea ca numai o singura radacina este reala. Daca q>0, atunci aceasta radacina este negativa; iar daca q<0 atunci ea este pozitiva .

Sa dovedim aceste fapte.Avem deci :

Fie acum p>0.Atunci:

si deci u este pozitiv ,iar      

este evident negativ.

Daca q>0, avem:

iar daca q<0, avem inegalitatea ,,pe dos".

Prin urmare ,daca q>0, atunci si deci va fi negativ; daca q<0 atunci si deci va fi pozitiv .

Sa vedem ce se intampla daca p<0. Ei bine, situatia se mentine, deci concluzia enuntata mai sus ramane valabila.

3)CAZUL <0 furnizeaza trei radacini reale distincte .

Demonstratia e relativ simpla , dar nu banala.

Daca <0, atunci fie

(A real pozitiv), atunci:

Intrucat avem de-a face cu un numar complex,

,

sa-ncercam sa-l scriem sub forma trigonometrica.

Evaluam mai intai modulul:

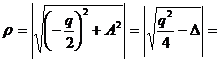
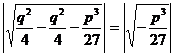
Functiile argumentului sunt :

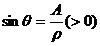
Asadar:

, unde k=0,1,2.

Se observa deci ca modulul lui u este

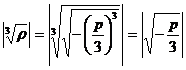
Patratul sau este . Dar deci implicit v=u, deoarece stim ca in general .

Asadar :

In final, se obtin solutiile ecuatiei de gradul III sub forma trigonometrica:

unde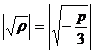

Dupa cum bine se vede, x₁, x₂ , x₃ R si x₁ x₂ x₃. In plus, daca q>0 avem doua radacini pozitive , iar daca q<0 avem o singura radacina pozitiva.

Direct se procedeaza astfel: se considera binecunoscuta formula:

care se scrie si asa:

Se alege ca necunoscuta x = in x³ +px+q=0 si se obtine:

Identificand cele doua ecuatii gasim imediat:

Prima relatie este satisfacuta daca se ia:

In timp ce a doua ne furnizeaza:

Existenta ,,legala" a lui este asigurata daca p<0 si:

Dar aceasta din urma relatie se mai scrie:

sau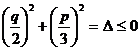

Evident, <0 trebuie sa implice p<0, deci solutii sub forma trigonometrica nu se pot da decat in cazul <0.

EXEMPLU (Kahane ,1958): Sa se rezolve trigonometric ecuatia

x³ -21x-20=0

Formula lui Cardano ne da:

unde

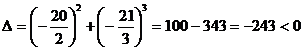
Se va alege :

in care:

,

Asadar:

si

unde k=0,1,2.

Radacinile sunt deci:

Avem:

Rezulta din tabele :

Atunci :

Exista si alte metode de rezolvare a ecuatiei de gradul III.

Intr-un curs mai vechi de algebra al lui Niewenglowski(1921)am gasit un procedeu care foloseste asa-numitul ,,Hessian" al polinomului de gradul III.

LODOVICO FERRARI

si infrangerea ecuatiei de gradul IV

Rezolvarea ecuatiei complete de gradul IV are loc relativ cam in aceeasi perioada cu aceea a ecuatiei de gradul III.

Conform scrierilor istorice,Cardano infiaza practic pe un elev al sau ,pe nume Lodovico Ferrari din Bologna ,talent ,matematic de mare forta.

Ferrari(1522-1565), a fost, in limbaj modern, asistentul lui Cardano.L-a insotit pe acesta in calatoriile sale stiintifice, l-a ajutat in redactarea monumentalei ,,Ars Magna" in care de fapt Cardano a si inclus metoda lui Ferrari de rezolvare a ecuatiei de gradul IV.

Ferrari a ajuns la solutia generala a ecuatiei de gradul IV tot in urma unei intreceri publice.

Conform cu Pietro Cossali(1748-1815), care a scris prin 1797 o istorie a algebrei, Giovanni Colla a propus lui Tartaglia o problema ce conduce la urmatorul sistem de ecuatii:

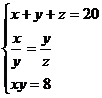
Prin eliminarea lui y si z, Tartaglia obtine ecuatia de gradul IV

Venind in contact cu disputa intre Colla si Tartaglia ,Cardano il atrage pe Ferrari in rezolvarea problemei. Acesta o rezolva in timp record, Cardano avand timpul necesar sa includa metoda in celebra ,,Ars Magna" (1545).

Practic, Ferrari a considerat o ecuatie de tipul:

p, q, n R

pe care, dupa o serie de artificii convenabile, o aduce la o asa-numita rezolventa de gradul III:

Sa consideram acum ecuatia de gradul IV sub forma uzuala:

x⁴ +px² +qx+r=0

Pentru orice real, are loc identitatea:

Il vom determina pe astfel incat sa aiba loc relatia:

(adica discriminantul trinomului din paranteza dreapta sa fie nul).

Ecuatia respectiva este de gradul III (rezolventa 1), deci odata determinat se poate scrie:

Asadar ecuatia de gradul IV se reduce la

sau adica la doua ecuatii simple de grad II .

Consideram polinomul general de grad IV P(x)=x⁴ +ax³ +bx² +cx+d si dorim sa-l transformam astfel ca acesta sa poata fi scris ca diferenta a doua patrate perfecte:

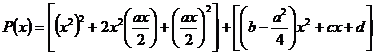
sau

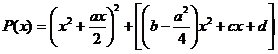
Introducem o necunoscuta auxiliara z in felul urmator :

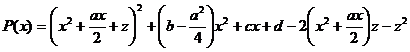
sau inca:

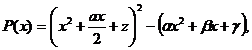
unde evident:

Bineinteles, polinomul este un patrat perfect, daca adica:

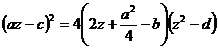
care nu este altceva decat rezolventa in cazul general.

Facem o observatie interesanta: daca z₀ este o radacina rationala a rezolvantei de mai inainte si expresiile:

sunt numere rationale, atunci polinomul P(x)= x⁴ +ax³ +bx² +cx+d este reductibil in campul numerelor rationale.

EXEMPLU: fie polinomul P(x)=6x⁴ -7x³ +x² -2.

Consideram polinomul inrudit :

si alcatuim rezolvarea acestuia:

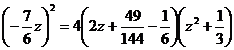
sau, prin substitutia 2z=u, obtinem rezolventa 180u³ -18u² +144u+25=0

Aceasta ecuatie are radacina rationala deci

Calculam pe rand expresiile:

Polinomul nostru se poate scrie in final ,

deci este reductibil.

TRUICA GEORGIANA MADALINA