Transformari omotetice

Fie o dreapta orientata d si un numar real nenul u. Daca fixam un punct W I d, atunci transformarea ce asociaza fiecarui punct O I d punctul M definit de relatia

WM = u WO (H)

se numeste omotetie de centru W si raport u pe d. Daca u > 0, omotetia este directa, iar daca u < 0, se numeste indirecta. Omotetia inversa omotetiei (H) asociaza fiecarui punct M I d punctul O definit de relatia

WO = WM (H')

Daca presupunem definit un sistem de coordonate S : d R cu originea W si notam coordonatele punctelor O si M cu t = S(O), s = S(M), atunci omotetiile (H) si (H') au reprezentarea analitica

s = u t

si respectiv

t = s

Omotetia poate fi privita ca o miscare. De exemplu, sa consideram punctul O' definit de relatia

OO' = a OM (H₁)

a fiind un numar pozitiv subunitar. Daca fixam punctul A dat de egalitatea

OA = OM

si definim sistemul de coordonate S_A : d R cu proprietatea S_A(O) = 0, S_A(A) = 1, atunci punctelor O' si M li se asociaza coordonatele s₁ = S_A(O'), s = S_A(M) intre care exista relatia

s₁ = a s (*)

aceasta fiind expresia analitica a omotetiei (H₁) de centru O si raport a in sistemul de coordonate S_A. Pe de alta parte, daca in (*) efectuam schimbarea de coordonate

s = u t (**)

si notam v = a u, atunci (*) devine

s₁ = v t (***)

Prin ultimele doua relatii, omotetia (H₁) de centru O si raport a = depinde de coordonata t = S(O). Daca t parcurge multimea R₊ a numerelor reale pozitive, atunci punctele O, O' si M parcurg semidreapta pozitiva cu originea W in sistemul de coordonate S, iar punctele O' si M parcurg semidreapta pozitiva cu originea O in sistemul de coordonate S_A. Deci putem vorbi de o miscare (deplasare) duala a punctelor O, O', M - sau a omotetiei (H₁) - pe dreapta d. Deplasarea "externa" a omotetiei (H₁) in sistemul de referinta S o numim "absoluta", iar deplasarea "interna" a omotetiei (H₁) in sistemul de coordonate S_A o numim "relativa".

Asa cum rezulta din relatiile (**) si (***), in sistemul de coordonate S_A miscarea se exprima prin doua tipuri de coordonate, unele variabile, dependente de punctul caruia i se asociaza si altele fixe, independente de aceste puncte. Este vorba despre coordonatele s = S_A(M), s₁ = S_A(O') si respectiv t = S(O). Pe de alta parte, in primul caz unitatile de masura au valori fixe, independente de punctele considerate, iar in al doilea caz acestea au valori variabile, care depind de punctele considerate. Este vorba despre unitatea de masura cu valoare unitara definita in sistemul de coordonate S_A si respectiv de unitatile de masura de marime v si u care au rezultat in urma schimbarilor de coordonate. Mai precis, daca pe multimea S a segmentelor definim o masura S_m : S R₊ cu proprietatea S_m(OO) = 0, S_m(OA) = 1, atunci in cazul unitatii de masura m = OA definita de punctul unitate A avem S_m(m) = 1, iar in cazul unitatilor de masura definite de relatiile

h = OM, h₁ = OO'

din (**), (***) si relatiile

OM = s m = t h, OO' = s₁ m = t h₁

rezulta h = u m, h₁ = v m, deci S_m(h) = u, S_m(h₁) = v.

Daca unitatile de masura si coordonatele fixe le numim "absolute", iar pe cele care depind de punctul considerat le numim "relative", atunci putem afirma ca miscarea in sistemul de coordonate S_A se exprima atit printr-un numar relativ de unitati absolute, cit si printr-un numar absolut de unitati relative. Aceasta reprezentare duala a miscarii relative a omotetiei (H₁) definita de punctele O, O', M in sistemul de coordonate S_A este datorata faptului ca omotetia (H) include (subordoneaza) omotetia (H₁). Daca nu tinem cont de aceasta subordonare, atunci utilizam relatiile (*) pentru a exprima analitic omotetia (H₁).

Putem relua observatiile de mai sus, daca ne referim la omotetia inversa (H'). De exemplu, daca fixam punctul B dat de egalitatea

OB = OM

si definim sistemul de coordonate T_B : d R cu proprietatea T_B(O) = 0, T_B(B) = 1, atunci punctelor O' si M li se asociaza coordonatele t₁ = T_B(O'), t = T_B(M) intre care exista relatia

t₁ = a t (*')

aceasta fiind expresia analitica a omotetiei (H₁) de centru O si raport a in sistemul de coordonate T_B. Pe de alta parte, daca in (*') efectuam schimbarea de coordonate

t = s

si avem in vedere ca a = , atunci (*') devine

t₁ = s

Prin ultimele doua relatii, omotetia (H₁) de centru O si raport a = depinde de coordonata s = S(M). Daca s parcurge multimea R₊ a numerelor reale pozitive, atunci punctele O' si M parcurg semidreapta pozitiva cu originea O in sistemul de coordonate T_B, iar omotetia (H₁) parcurge semidreapta pozitiva cu originea W in sistemul de coordonate S. Deci putem vorbi de o miscare absoluta a omotetiei (H₁) pe dreapta d, exprimata prin coordonata absoluta s = S(M), cit si de o miscare relativa a omotetiei (H₁) pe dreapta d, exprimata prin coordonatele relative t₁ = s si t = s.

Reluam observatiile de mai sus, pornind de la un segment oarecare OM I d. Fie o dreapta orientata d si fie puctele O < A < B I d. Daca pe dreapta d definim un sistem carezian de coordonate S_A : d R cu proprietatea S_A(O) = 0, S_A(A) = 1, cit si un sistem cartezian de coordonate T_B : d R cu proprietatea T_B(O) = 0, T_B(B) = 0, iar pe multimea S a segmentelor definim o masura S_m : S R₊ cu proprietatea S_m(OO) = 0, S_m(OA) = 1, cit si o masura T_h : S R₊ cu proprietatea T_h(OO) = 0, T_h(OB) = 1, atunci spunem ca pe dreapta d am definit un sistem de referinta cu originea O, sau ca punctului O i-am asociat un sistem de referinta. Notam cu S acest sistem de referinta si cu m = OA, h = OB unitatile de masura definite de punctele unitate A si B.

Intr-un sistem de referinta exista urmatoarea relatie de echivalenta intre unitatile de masura definite in sistemul de referinta respectiv si coordonatele care se asociaza unui punct: fixarea in mod arbitrar a unitatilor de masura si determinarea in mod canonic a coordonatelor este echivalent cu fixarea in mod arbitrar a coordonatelor si determinarea in mod canonic a unitatilor de masura.

Intr-adevar, daca notam cu s = S_A(M), t = T_B(M) coordonatele care se asociaza unui punct M de pe semidreapta pozitiva cu originea O, atunci segmentului OM i se asociaza masurile s = S_m(OM), t = T_h(OM) si putem scrie

OM = s m = t h (a)

intre unitatile de masura m, h exista relatiile

h = u m, m = h (b)

unde u = S_m(h), = T_h(m), iar conform (a) si (b) rezulta ca intre coordonatele s, t exista relatiile

s = u t, t = s (1)

Invers, din (a) si (1) rezulta (b), deci schimbarile de unitati de masura (b) sint echivalente cu schimbarile de coordonate (1).

Unitatile de masura fixate in mod arbitrar sint definite de punctele unitate A si B din sistemele de coordonate S_A si respectiv T_B, iar coordonatele determinate in mod canonic sint coordonatele s = S_A(M), t = T_A(M). Coordonatele "importate" fixate pe axele de coordonate ale sistemelor carteziene S_A si T_B, t si respectiv s, cit si unitatile de masura h si respectiv m definite de acestea (h este un segment de marime u determinat de coordonata t pe axa sistemului cartezian S_A, iar m este un segment de marime determinat de coordonata s pe axa coordonatelor sistemului cartezian T_B), reprezinta cordonatele fixate in mod arbitrar si respectiv unitatile de masura determinate in mod canonic.

Prin "schimbarea" unitatilor de masura sau a coordonatelor se inlocuieste, in dublu sens, un anumit tip de unitati de msura sau coordonate cu un alt tip de unitati de masura si respectiv coordonate. Daca utilizam termenii de "relativ" si "absolut" in loc de "determinat in mod canonic" si respectiv de "fixat in mod arbitrar", atunci putem afirma ca intr-un sistem de referinta, un segment se reprezinta atit printr-un numar relativ de unitati absolute, cit si printr-un numar absolut de unitati relative. Un exemplu, in acest sens, este segmentul OM descris de relatiile (a). Un alt exemplu este dat in continuare.

Sa consideram segmentul OO' I OM definit de relatia

OO' = a OM (H₁)

unde a este un numar pozitiv subunitar. Daca amplificam relatiile (a), (b) si (1) cu factorul a si efectuam notatiile m₁ = a m, h₁ = a h, s₁ = a s, t₁ = a t, v = a u, atunci segmentul OO' se reprezinta printr-un numar relativ de unitati absolute si printr-un numar absolut de unitati relative conform relatiilor

OO' = s₁ m = t h₁, OO' = t₁ h = s m₁ (a₁)

unde unitatile de masura relative se exprima in functie de cele absolute conform relatiilor

h₁ = v m , m₁ = h (b₁)

iar coordonatele relative se exprima in functie de cele absolute conform relatiilor

s₁ = v t, t₁ = s (2)

Sa mai remarcam ca daca schimbam originea sistemului de referinta S din punctul O in punctul O', atunci coordonatele s₂, t₂ care se asociaza punctului M in raport cu noua origine a sistemului de referinta S sint date de relatiile

s₂ = s - v t, t₂ = t - s (3)

Desigur ca exista un punct W < O si un sistem de coordonate S : d R cu originea in punctul W astfel ca punctele W, O si M definesc omotetiile de centru W exprimate de relatile

WM = u WO, WO = WM (H)

avind reprezentarea analitica (1) in sistemul de coordonate S. Daca notam cu m unitatea de masura in cazul sistemului de coordonate S, aceasta poate fi determinata pe baza relatiei

s m = (s - t) m

sau, echivalent, pe baza relatiei

t h = (s - t) m

acestea rezultind pe baza egalitatii

OM = WM - WO

in care am tinut cont de (a) si de faptul ca WO = t m, WM = s m.

Se constata ca daca pornim de la un segment arbitrar OM I d, prin intermediul sistemului de referinta S asociat puctului O putem determina omotetiile din care face parte acest segment - in acest caz am pus in evidenta omotetiile de centru W si raport u si respectiv , definite de relatiile (H) in sistemul de coordonate S, cit si omotetiile de centru O si raport a = definite de relatia (H₁) in sistemele de coordonate S_A, T_B.

Vom spune ca in sistemul de referinta S fixat prin coordonatele absolute t = S(O), s = S(M), schimbarile de coordonate (1), (2) si (3) definesc miscarea relativa a punctelor O', M in in raport cu punctul O, respectiv miscarea relativa a punctului M in raport cu punctul O' in sistemele de cordonate S_A si T_B cu originea O.

Relatiile (3) au fost deduse in ipoteza ca O < O' si deci O'M = OM - OO'. Daca am fi pornit de la ipoteza ca O' < O (in cazul omotetiei (H₁) indirecte, a < 0), atunci ar fi trebuit sa luam in considerare egalitatea

O'M = O'O + OM (~)

si am fi obtinut relatiile

s₂ = s + v t, t₂ = t + s (3₁)

in locul relatiilor (3). Putem sa exprimam acest caz, daca schimbam punctele O si O' intre ele, adica punctul O il notam cu O', iar punctul O' il notam cu O. Ca urmare, relatia (~) devine

OM = OO' + O'M

iar relatia (H₁) se scrie

OO' = a O'M (H₂)

In acest caz, sistemul de referinta asociat punctului O' il notam cu S', acesta fiind definit de sistemele de coordonate S'_A, T'_B cu originea O', iar coordonatele s, t, s₁, t₁, s₂ si t₂ le notam cu s', t', s'₁, t'₁, s'₂ si respectiv t'₂ (unitatile de masura m, h nu sint afectate de aceste notatii). Va rezulta ca in sistemul de referinta S' asociat punctului O', fixat prin coordonatele absolute t' = S(O'), s' = S(M) in sistemul de coordoate S cu originea W, schimbarile de coordonate

s' = u t', t' = s' (1')

si respectiv

s'₁ = v t', t'₁ = s' (2')

definesc miscarea relativa a punctelor O, M in raport cu punctul O' in sistemele de cordonate S'_A si T'_B cu originea O', iar schimbarile de coordonate

s'₂ = s' + v t', t'₂ = t' + s' (3')

definesc miscarea relativa a punctului M in raport cu punctul O in aceste sisteme de coordonate. Acum putem compara coordonatele asociate punctului M in raport cu punctul O in sistemele de referinta S si S', asadar coordonatele s, t date de (1) cu coordonatele s'₂, t'₂ date de (3') (in cazul relatiilor (3) si (3₁), aceasta comparare ar fi fost mai dificila). Va rezulta sistemul de ecuatii

s = k (s' + v t'), t = k (t' + s') (4)

care, rezolvat in raport cu s', t', conduce la solutiile

s' = k (s - v t), t' = k (t - s) (4')

daca factorul k are valoarea

k = 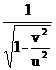(5)

Constatam ca daca factorul k are valoarea data de (5), atunci ecuatiile (4) sint solutiile sistemului de ecuatii (4'). Pe de alta parte, constatam ca (4') sint relatiile dintre coordonatele s', t' si s₂, t₂ asociate punctului M in raport cu punctul O' in sistemele de de coordonate S' si respectiv S. In concluzie, transformarle omotetice (4) si (4') exprima legatura dintre omotetiile distincte (H₁) si (H₂), diferenta dintre acestea constind in faptul ca una este reala si cealalta virtuala, deci una dintre aceste omotetii exita in realitate, iar cealalta exista doar ca posibilitate.

Exemplu. Daca presupunem ca O, O', M sint trei puncte materiale aflate in miscare uniform-rectilinie pe o directie comuna, care au pornit in acelasi moment de timp si din acelasi loc din spatiu, astfel ca punctele O' si M se deplaseaza in acelasi sens in sistemul de referinta S asociat punctului O, iar punctele O si M se depaseaza in sensuri opuse in sistemul de referinta S' asociat punctului O', atunci putem utiliza relatiile de mai sus pentru descrierea acestor miscari, respectiv relatiile (1), (2) (3) si (1'), (2'), (3'). In primul caz, intre punctele O, O', M exista intervalele spatiu-tip (s, t), (s₁, t₁), (s₂, t₂) in locul-moment (s, t) in care se afla sistemul de referinta S, iar in al doilea caz, intre acestea exista intervalele spatiu-timp (s', t'), (s'₁, t'₁), (s'₂, t'₂) in locul-moment (s', t') in care se afla sistemul de referinta S'. In aceste cazuri, sistemului de referinta ii atribuim dublul rol de instrument de masura atit pentru spatiu, cit si pentru timp. Prin urmare, pe axa coordonatelor sistemului de referinta reprezentam atit coordonatele de spatiu, acestea fiind determinate de un segment m considerat unitate de masura pentru spatiu, cit si coordonatele de timp, acestea fiind determinate de un segment h considerat unitate de masura pentru timp. Asa cum am remarcat, intr-un sistem de referinta raportul unitatilor de masura este egal cu raportul coordonatelor asociate unui punct si poate fi orice numar real - deci daca fixam mai intii unitatile de masura (caz in care se presuupun necunoscute coordonatele), determinam ulterior coordonatele respective, iar daca fixam mai intii coordonatele (caz in care coordonatele se presupun cunoscute), determinam ulterior unitatile de masura. De exemplu, daca sint cunoscute coordonatele asociate punctului M, raportul acestora fiind un numar c > u, atunci schimbarea de coordonate s = c t implica schimbarea de unitati de masura h = c m. Ca urmare, unul dintre segmentele m = OA sau h = OB va avea o marime diferita de cele considerate in cazul precedent (in care s = u t).

Intr-un exemplu concret, sistemele de referinta S si S' pot fi considerate o sosea rectilinie si o platforma care se deplaseaza pe sosea cu viteza constanta v, iar punctul M, un observator care se deplaseaza in acelasi sens cu platforma, cu viteza constanta u pe sosea - caz in care acesta va avea viteza u - v fata de platforma, sau cu viteza u pe platforma - caz in care acesta va avea viteza u + v fata de sosea. Alegerea variantei de deplasare cu viteza constanta u - pe sosea sau pe platforma - este o decizie a observatorului pe care acesta o poate lua atit in locul-moment initial (in care incepe miscarea), cit si in orice alt loc-moment. Asa cum se constata din relatiile (4), (4'), intervalul spatiu-timp real parcurs de observator intr-un sistem de referinta poate fi cel mult proportional cu intervalul spatiu-timp virtual parcurs de observator intr-un alt sisem de referinta. Din acest motiv, schimbarea sistemului de referinta - sau trecerea dintr-un sistem de referinta in altul - afecteaza (fizic) observatorul cu factorul de inertie k dat de (5).