Notiunea de lege de compozitie prezinta un mare grad de generaliate.
In definitia unei legi de compozitie j pe o multime M se ignora atat natura elementelor multimii M cat si modul efectiv in care j actioneaza pe M+M. Singura restricti pusa este ca j sa asocieze la un cuplu ordonat (x, y) de elemente din M un element j(x, y) din M si numai unul. Din acest motiv studiul legilor de compozitie bazat doar pe definitia lor este foarte sarac in rezultate. S-a dovedit fertila ideea de a studia legi de compozitie ce au proprietati care pot fi semnalate in multe exemple concrete.
Asociativitatea
![]()
Vom presupune in
continuare ca M este o multime nevida echipata cu o lege de compozitie ,,*'',
Expresia x*y se citeste : x compus cu y sau x stea y.
Definitiile si rezultatele vor fi date folosind aceasta notatie urmand sa fie facute precizarile ce se impun si in alte notatii pentru legea de compozitie
Fie x,y,z apartinand lui M. Prezenta parantezelor in expresia (x*y)*z cere urmatoarea procedura de calcul: se afla intai compusul lui x cu y si apoi x*y se compune cu z, obtinandu-se in final elementul (x*y)*z care apartine lui M. Prezenta parantezelor in expresia x*(y*z) impune sa aflam intai y*z si sa-l compunem apoi cu x, obtinandu-se astfel elementul x*(y*z) care apartine lui M.
Definitie: O lege de compozitie M+M cu vaori in M, (x,y) cu valori in x*y se numeste asociativa daca:
(x*y)*z=x*(y*z), ( x,y,z apartinand lui M.
Daca legea de compozitie este data in notatie aditiva (multiplicativa) atunci proprietatea de asociativtate a acesteia se scrie:
(x+y)+z=x+(y+z)
respectiv
(x y) z=x (y z) ( ) x,y,z apartinand lui M.
Exemple:
1.Adunare si inmultirea numerelor reale sunt legi de compozitie asociative pentru ca:
(x+y)+z=x+(y+z) si (x y) z=x (y z).
2.Adunarea si inmultirea matricilor din M (R) sunt legi de compozitie asociative, caci:
(A+B)+C=A+(B+C) si (AB)C=A(BC).
3.Reuniunea si intersectia partilor unei multimi E sunt legi de compozitie asociative, caci:
(XUY)UZ=XU(YUZ).
4.Compunerea functiilor unei multimi E in ea insasi este o lege de compozitie asociativa, caci:
(f*g)*h=f*(g*h).
Comutativitatea
Proprietatea de asociativitate largest mult aria posibilitatilor in perfectarea calcului algebric. O alta sursa in acest sens este data de legile de compozitie pentru care produsul a doua elemente oarecare este independent de ordinea in care se face compunerea acestora. Mai precis:
Definitie: O lege de compozitie M+M cu valori in M, (x, y) cu valori in x*y
se numeste comutativa, daca:
x*y=y*x, ( ) x,y e M.
Adunarea si inmultirea numerelor reale,reuniunea si intersectia partilor unei multimi sunt legi de compozitie comutative.
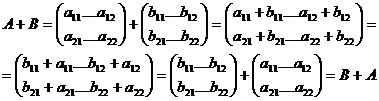
Numeroase legi de compozitie se
definesc cu ajutorul altora deja cunoscute. Asemenea operatii pot prelua unele
proprietati de la cele de plecare prin mecanismul dat chiar de definitia lor.
Astfel comutativitatea adunariimatricelor din M (R) este o consecinta a proprietatii de
comutativitate a adunarii numerelor reale. Intradevar, daca A, B apartin lui M (R), A=(aij), B=(bij), atunci:
Sa observam ca inmultirea matricilor din M (R) nu este comutativa,cu toate ca inmultirea numerelor reale este comutativa. Aceasta rezulta din exemplul urmator:
![]()
Deci daca A,B e M (R) atunci A B B A.
Element neutru
Numerele reale 0 si 1 au pruprietatiile:
0+x=x+0=x, ( ) xeR,
respectiv
1 x=x 1=x, ( ) xeR.
Daca E este o multime si 1E:E E este aplicatia identica a lui E, atunci:
1E f=f E=f, ( ) feF(E).
De asemenea, pentru orice matrice A e M (R) avem:
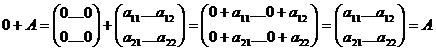
si analog A+0=A.
Definitie:Un element eeM se numeste element neutru pentru o lege de . compozitie M M M, (x, y) x*y, daca
e*x=x*e=x, ( ) xeM.
Teorema:Daca o lege de compozitie are element neutru, atunci acesta este unic.
Demonstratie:Fie e si e` doua elemente neutre pentru o lege de compozitie M M M, (x, y) x*y. Avem e*e`=e` caci e este element neutru.De asemenea, e*e`=e caci si e` este element neutru, de unde e=e`.
Asadar, elementul neutru,in caz ca exista,este unic determinat.
In notatie aditiva elementul neutru se noteaza de regula cu 0 si se numeste elementul zero, iar in notatie multiplicativa elementul neutru se noteaza cu 1 sau chiar cu e si poarta numelede elementul unitate. Avem
0+x=x+0=x, ( ) xeM,
respectiv
1 x=x 1=x, ( ) xeM.
Exemple:
1.Numarul real 0este elementul neutru al adunarii numerelor reale, numarul real 1 este elementul neutru al inmultirii numerelor reale.
2.Aplicatia identica 1E a multimii E este elementul neutru al operatiei de compunere a functiilor din F(E).
3.Multimea 2N= a numerelor naturale pare o parte stabila a lui N in raport cu inmultirea si legea de compozitie indusa de catre aceasta pe 2N nu admite element neutru.
Element simetrizabil
Ca si pana acum, Meste o multime nevida inzestrata cu o lege de compozitie
M M M, (x, y) x*y
Vom presupune in plus ca aceasta lege de compozitie este asociativa si ca admite element neutru, fie acesta e.
Definitie:Uu element xeM se numeste simetrizabil in raport cu legea de . compozitie (asociativa si cu element neutru) M M M,(x,y) x*y, . daca exista x`eM astfel incat:
x`*x=x*x`=e.
x``*x=x*x``=e
atunci x`=x``. Intr-adevar
x`=x`*e=x`*(x*x``)=(x`*x)*x``=e*x``=x``.
Daca xeM este simetrizabil, atunci unicul element x`eM cu proprietatea x`*x=x*x`=e se numeste simetricul lui x.
In notatia multiplicativa simetricul lui x, in caz ca exista, se noteaza de regula cu x` si se numeste inversul lui x; in notatia aditiva se noteaza cu -x si se numeste opusul lui x. Asadar,
x`x=xx`=1,
respectiv
(-x)+x=x+(-x)=0.
Exemple
1.Cum e*e=e, rezulta ca elementul neutru este si simetrizabil si simetricul lui e este tot e. In notatie multiplicativa avem 1`=1, iar in notatie aditiva -0=0.
2.Orice numar intreg este simetrizabil in raport cu adunarea numerelor intregi; numerele intregi simetrizabile fata de inmultire sunt 1 si -1, 1`=1,
3.Consultand tabla operatiilor induse pentru compunerea functiilor din F(E), unde E=, se observa ca e e=e si f f=e, deci functiile e si f sunt simetrizabile (inversabile) si e`=e, f`=f.
compozitie M M M,(x, y) x*y (asociativa si cu element neutru
atunci x*y si x` sunt simetrizabile.Mai mult:
1) (x*y)`=y`*x`,
(x`)`=x
Demonstratie:
Avem:
(y`*x`)*(x*y)=y`*(x`*(x*y))=y`*((x`*x)*y)=y`*(e*y)=y`*y=e
si analog (x*y)*(y`*x`)=e. Rezulta ca x*y este simetrizabil si (x*y)`=y`*x`. A doua afirmatie este imediata.
Proprietatile 1) si 2) din enuntul teoremei precedente se transcriu multiplicativ astfel:
1) (x y)`=y` x`, 2) (x`)`=x,
iar in notatia aditiva
1) -(x+y)=(-y)+(-x), 2) -(-x)=x.
![]()
Se face urmatoarea conventie de notatie
Aplicatii.
1.Pe multimea Z a numerelor intregi defnim legea de compozitie
Z Z Z, (x, y) x y=x+y-xy,
Numita compunerea circulara. Sa se arate ca legea de compozitie este asociativa si comutativa.
a)(x y) z=(x+y-xy) z=x+y-xy+z-(x+y-xy)z=x+y+z-xy-yz-zx+xyz
x (y z)=x (y+z-yz)=x+y+z-yz-x(y+z-yz)=x+y+z-xy-yz-zx+xyz
T(x y) z=x (y z)
b)x y=x+y-xy=y+x-yx=y x
2.Fie M si N doua multimi, * o lege de compozitie pe M, o lege de compozitie pe N si f:M N o functie surjectiva astfel incat
f(x*y)=f(x) f(y), ( ) x, y eM.
a)Daca legea de compozitie * este asociativa (comutativa) atunci legea de compozitie este asociativa (comutativa).
b)Functia f:Z Z, f(x)=1-x are proprietatea
f(xy)=f(x) f(y), ( ) x, y eZ
unde xy este produsul uzual in Z, iar este compunerea circulara.
a)Fie u, v, w eN.
f surjectiva T ) x, y, z eM a. i. u=f(x), v=f(y), w=f(z).
u v=f(x) f(y)=f(x*y)=f(y*x)=f(y) f(x)=v u
(u v) w=(f(x) f(y)) f(z)=f(x*y) f(z)=f((x*y)*z)=
=f(x*(y*z))=f(x) f(y*z)=f(x) (f(y) f(z))=u (v w)
b)( )x, y eZ T
Tf(x) f(y)=f(x)+f(y)-f(x)f(y)=1-x+1-y-(1-x)(1-y)=
=2-x-y-1+y+x-xy=1-xy=f(xy).
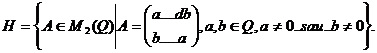
3.Fie d un numar intreg liber de patrate si:
a)H este o parte stabila a lui M (Q) in raport cu inmultirea matricelor.
b)( ) matrice AeH este inversabila in raport cu operatia indusa.
![]()
![]()
a)Fie A, B e
H,
![]()
a``=aa`+dbb` e Q, b``=ba`+ab` e Q
daca AB e HTa`` 0 sau b`` 0.
Pp. a``=0 si b``=0
Tx=a` si y=b` sol a sist:
![]()
d este liber de patrate si a 0 sau b 0 T det A 0 caci altfel d e Q.Contradic
Dar din det A 0 T sol sist este x=y=0
T a`` 0 sau b`` 0
T AB e H.
![]()
b)I e H si
A e
H. Arat ca exista X e
H
![]()
a.i. XA=AX=I

Cum a 0
sau b 0
Tx 0 sau
y 0.
Asadar:
Se verifica si egalitatea XA=I , deci A` exista si A`=X e H.
4.Fie M=N N.Pe multimea M introducem legile de compozitie:
(x, y)+(z, w)=(x+z, y+w),
(x, y)(z, w)=(xz+yw, xw+yz)
oricare ar fi perechile (x, y) si (z, w) din M. Aratati ca aceste legi de compozitie sunt asociative, comutative si cu element neutru.
Asociatiovitatea:
a=(x, y), b=(z, w), g=(u, t) e M.
,,+'' (a+b)+g=[(x+z, y+w)]+(u, t)=((x+z)+u, (y+w)+t)=(x+z+u, y+w+t)=
=(x+(z+u), y+(w+t))=(x, y)+(z+u, w+t)=a+(b+g)
,, '' (ab)g=(xz+yw, xw+yz)(u, t)=
=(xzu+ywu+xwt+yzt, xzt+ywt+xwu+yzu)
a(bg)=(x, y)(zu+wt, zt+wu)=
=(xzu+xwt+yzt+ywu, xzt+xwu+yzu+ywt)
Comutativitatea:
a+b=(x, y)+(z, w)=(x+z, y+w)=(z+x, w+y)=b+a
ab=(x, y)(z, w)=(xz+yw, xw+yz)=(zx+wy, wx+zy)=ba
Element neutru:
( ) e e M a.i. a+e =e +a=a, ( ) a e M
e =(0, 0) a+e =(x, y)+(0, 0)=(x, y)=a Te =(0, 0) el. Neutru pt ,,+''
( ) e e M a.i. ae =e a=a, ( ) a e M
e =(1, 0) ae =(x, y)(1, 0)=(x, y)=a Te =(1, 0) el. Neutru pt ,, ''
5.Fie a, b, c e Z, b 0. Pe Z definim legea de compozitie ,,*''
x*y=axy+b(x+y)+c, ( ) x, y e Z.
a)Aratati ca * este lege de compozitie asociativa daca si numai daca
![]()
b)Cand are loc a) legea de compozitie * are el. Neutru daca si numai daca b/c.
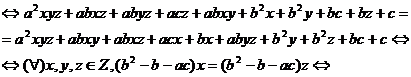
a)* asociativa
( )
x, y, z e
Z, (x*y)*z=x*(y*z)
![]()
b),,T''( ) e e Z
a.i. x*e=e*x=x, ( )
x e
Z
Tx*e=x
axe+b(x+e)+c=x
(ae+b-1)x+be+c=0
Tae+b-1=0 si be=-c Te=-c/b e Z Tb divide pe c.
,, ''( ) k e Z a.i. c=kb, ( ), x e Z,
x*(-k)=-axk+b(x-k)+c=x(-ak+b)+c-kb=x(-ac/b+b)=
=x(b-ac)/b=xb/b=x
T -k el. neutru.
6.Pe R se defineste letea de compozitie
*:R R R, (x, y) x*y=xy+2ax+by.
Determinati a si b astfel incat legea de compozitie sa fie comutativa si asociativa.
* comutativa
Tx*y=y*x xy+2ax+by=yx+2ay+bx
2a(x-y)=b(x-y)
2a=b
* asociativa
T(x*y)*z=x*(y*z)
(x*y)*z=[xy+bx+by]*z=xyz+bxy+byz+b(xy+bx+by+z)=
=xyz+bxz+byz+bxy+b x+b y+bz.
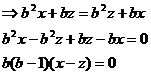
x*(y*z)=x*[yz+by+bz]=xyz+bxy+bxz+bx+byz+b y+b z.
Tb=0 sau b=1
Ta=0, b=0
a=1/2, b=1.
7.Pe R = definim legile de compozitie:
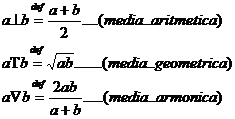
Aratati ca aceste legi de3 compozitie sunt comutative si nu sunt asociative. Admit element neutru?
Comutativitatea
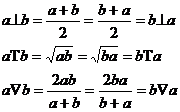
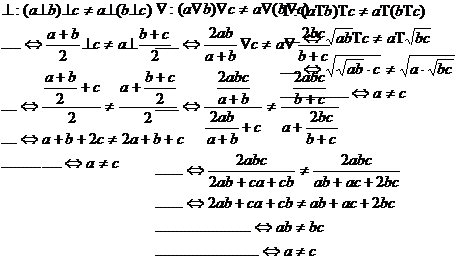
Non asociativitatea
Element neutru:
:( ) e e R a.i. a e=e a=a, ( ) a e R
T(a+e)/2=a
Ta+e=2a
Te=a fals, a variabil, e unic.
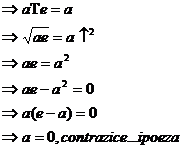
T:( )
e e
R a.i. aTe=eTa=a, ( )
a e
R
8.Pe M (R) se defineste legea de compozitie *
A*B=AB+BA, ( ) A,B e M (R)
Studiati daca legea de compozitie * este asocitiva, comutativa si daca admite element neutru.
asociativitatea
(A*B)*C=(AB+BA)*C=ABC+BAC+CAB+CBA
A*(B*C)=A*(BC+CB)=ABC+ACB+BCA+CBA
(A*B)*C A*(B*C)
T* nu este asociativa
comutativitatea
A*B=AB+BA=BA+AB=B*A
T* este comutativa
el. neutru
( ) E e M (R) a.i. A*E=E*A=A, ( ) A e M (R)
A*E=A
TAE+EA=A
TE=I /2.
9.Fie n>0 un numar intreg si
M=
a)Daca (a, b), (c, d) e MT(ac, ad+bc) e M
b)Legea de compozitie * definita pe M prin:
(a, b)*(c, d)=(ac, ad+bc)
este comutativa si asociativa.
c)Determinati elementul neutru si elementele simetrizabile.
a)(a, b) e M; (c, d) e M; a,b,c,d e Z
(a, n)=1 T (c, n)=1
a e Z; c e Z T ac e Z T(ac, n)=1
a e Z; d e Z; b e Z; c e Z Tad+bc e Z
T(ac, ad+bc) e M
b)(a, b)*(c, d)=(ac, ad+bc)=(ca, cb+da)=(c, d)*(a, b)
T* este comutativa
[(a, b)*(c, d)]*(g, h)=(ac, ad+bc)*(g, h)=(acg, ach+adg+bcg)
(a, b)*[(c, d)*(g, h)]=(a, b)*(cg, ch+dg)=(acg, ach+adg+bcg)
T* este asociativa
c)el. neutru
( ) e=(x, y) e M a.i. (a, b)*(x, y)=(x, y)*(a, b)=(a, b), ( ) (a, b) e M
(a, b)*(x, y)=(a, b)
(ax, ay+bx)=(a, b)
Tax=a T x=1
Tay+bx=b Tay+b=b Tay=0 Ty=0
T(x, y)=(1, 0)
el. simetrizabil
( ) (a, b) e M, ( ) (a`, b`) e M a.i. (a, b)*(a`, b`)=(1, 0)
(aa`, ab`+ba`)=(1, 0)
Taa`=1 Ta`=1/a a` e Z Ta`= 1
Tab`+ba`=0 Tb`=b
T(a`, b`)=( 1,b)