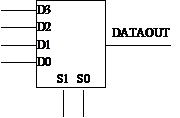ANALIZA ŞI SINTEZA DISPOZITIVELOR NUMERICE

curs
Bibliografie

1. Circuite de comutare aplicate în calculatoarele electronice, V. Pop, Volker Popovici, ed. Facla, 1976

2. Circuite integrate digitale, Gh. Ştefan, I. Drăghici, T. Mureşan, E. Barbu, EDP, 1983

3. De la poarta TTL la microprocesor, I. Sztojanov ş.a., ET, 1987

4. Proiectarea cu circuite logice MSI şi LSI standard, T.R. Blakeslee, ET, 1988

5. Circuite integrate digitale, Gh. Stefan, V. Bistriceanu, Probleme, proiectare, EDP, 1992

6. Circuite integrate digitale, Gh. Stefan, V. Bistriceanu, Probleme, proiectare, Ed. Albastră, 2000

7. Automatizări discrete în industrie, Culegere de probleme, N. Sprânceană, R. Dobrescu, Th. Borangiu, ET, 1978

8. Sisteme numerice cu circuite integrate, Culegere de probleme, Sanda Maican, ET, 1980

9. Analiza şi sinteza dispozitivelor numerice, I.A. Leţia, Îndrumător de laborator, I.P. Cluj-Napoca, 1985

10.Analiza şi sinteza dispozitivelor numerice, A. Neţin, O. Creţ, Îndrumător de laborator, UT Press. Cluj-Napoca, 1998

Curs 1

CAPITOLUL I

ELEMENTE DE ALGEBRĂ BOOLEANĂ

1.1. Generalităţi

Transferul, prelucrarea şi păstrarea datelor numerice sau nenumerice în interiorul unui calculator se realizează prin intermediul circuitelor de comutare. Aceste circuite se caracterizează prin faptul că prezintă două stări stabile care se deosebesc calitativ între ele. Stările sunt puse în corespondenţă cu valorile binare “0” şi “1” sau cu valorile logice “adevărat” şi “fals” (din acest motiv se mai numesc şi circuite logice). Pornind de la aceste considerente, un domeniul al logicii matematice, (ştiinţa care utilizează metode matematice în soluţionarea problemelor de logică) numit “algebra logicii” şi-a găsit o largă aplicare în analiza şi sinteza circuitelor logice. Algebra logicii operează cu propoziţii care pot fi adevărate sau false. Unei propoziţii adevărate i se atribuie valoarea “1”, iar unei propoziţii false i se atribuie valoarea “0”. O propoziţie nu poate fi simultan adevărată sau falsă, iar două propoziţii sunt echivalente d.p.d.v. al algebrei logice, dacă simultan ele sunt adevărate sau false. Propoziţiile pot fi simple sau compuse, cele compuse obţinându-se din cele simple prin legături logice de tipul conjuncţiei Ù, disjuncţiei Ú sau negaţiei Ø.

Bazele algebrei logice au fost puse de matematicianul englez George Boole (1815-1864) şi ca urmare ea se mai numeşte şi algebră booleană. Ea a fost concepută ca o metodă simbolică pentru tratarea funcţiilor logicii formale, dar a fost apoi dezvoltată şi aplicată şi în alte domenii ale matematicii. În 1938 Claude Shannon a folosit-o pentru prima dată în analiza circuitelor de comutaţie.

1.2. Definirea axiomatică a algebrei booleene

Algebra booleană este o algebră formată din:

- elementele {0,1};

- 2 operaţii binare numite SAU şi SI, notate simbolic + sau Ú şi × sau Ù;

- 1 operaţie unară numită NU negaţie, notată simbolic sau Ø.

Operaţiile se definesc astfel:

SI SAU NU

0 × 0 = 0 0 + 0 = 0 0 = 1

0 × 1 = 0 0 + 1 = 1 1 = 0

1 × 0 = 0 1 + 0 = 1

1 × 1 = 1 1 + 1 = 1

Axiomele algebrei booleene sunt următoarele:

Fie o mulţime M compusă din elementele x₁, x₂,…x_n, împreună cu operaţiile × şi +. Această mulţime formează o algebră dacă:

1) Mulţimea M conţine cel puţin 2 elemente distincte x₁ ¹ x₂ (x₁,x₂Î M);

2) Pentru " x₁ Î M, x₂ Î M avem:

x₁ + x₂ Î M şi x₁ × x₂ Î M

3) Operaţiile × şi + au următoarele proprietăţi:

a. sunt comutative

x₁ × x₂ = x₂ × x₁

x₁ + x₂ = x₂ + x₁

b. sunt asociative

x₁ × (x₂ × x₃) = (x₁ × x₂) × x₃

x₁ + (x₂ + x₃) = (x₁ + x₂) + x₃

c. sunt distributive una faţă de cealaltă

x₁ × (x₂ + x₃) = x₁ × x₂ + x₁ × x₃

x₁ + (x₂ × x₃) = (x₁ + x₂) × (x₁ + x₃)

4) Ambele operaţii admit câte un element neutru cu proprietatea:

x₁ + 0 = 0 + x₁ = x₁

x₁ × 1 = 1 × x₁ = x₁

unde 0 este elementul nul al mulţimii, iar 1 este elementul unitate al mulţimii.

5) Dacă mulţimea M nu conţine decât două elemente, acestea trebuie să fie obligatoriu elementul nul 0 şi elementul unitate 1; atunci pentru " x Î M există un element unic notat cu x cu proprietăţile:

x × x = 0 principiul contradicţiei

x + x = 1 principiul terţului exclus

x este inversul elementului x.

În definirea axiomatică a algebrei s-au folosit diferite notaţii. În tabelul următor se dau denumirile şi notaţiile specifice folosite pentru diverse domenii:

Matematică	Logică	Tehnică
Prima lege de compoziţie x1 + x2	Disjuncţie x1 Ú x2	SAU x1 + x2
A doua lege de compoziţie x1 × x2	Conjuncţie x1 Ù x2	SI x1 × x2
Elementul invers x	Negare Øx	NU x

1.3. Proprietăţile algebrei booleene

Plecând de la axiome se deduc o serie de proprietăţi care vor forma reguli de calcul în cadrul algebrei booleene. Aceste proprietăţi sunt:

1) Principiul dublei negaţii

x = x dubla negaţie duce la o afirmaţie

2) Idempotenţa

x × x = x

x + x = x

3) Absorbţia

x₁ × (x₁ + x₂) = x₁

x₁ + (x₁× x₂) = x₁

4) Proprietăţile elementelor neutre

x × 0 = 0 x × 1 = x

x + 0 = x x + 1 = 1

5) Formulele lui De Morgan

x₁ × x₂ = x₁ + x₂

x₁ + x₂ = x₁ × x₂

Aceste formule sunt foarte utile datorită posibilităţii de a transforma produsul logic în sumă logică şi invers.

Formulele pot fi generalizate la un număr arbitrar de termeni:

x₁ × x₂ × … × x_n = x₁ + x₂ + … + x_n

x₁ + x₂ + … + x_n = x₁ × x₂ × … × x_n

6) Principiul dualităţii – dacă în axiomele şi proprietăţile algebrei booleene se interschimbă 0 cu 1 şi + cu ×, sistemul de axiome rămâne acelaşi, în afara unor permutări.

Verificarea proprietăţilor se poate face cu ajutorul tabelelor de adevăr şi cu observaţia că două funcţii sunt egale dacă iau aceleaşi valori în toate punctele domeniului de definiţie. Prin tabelul de adevăr se stabileşte o corespondenţă între valorile de adevăr ale variabilelor şi valoarea de adevăr a funcţiei.

Obs. Comutativitatea şi asociativitatea pot fi extinse la un număr arbitrar, dar finit, de termeni, indiferent de ordinea lor.

1.4. Funcţii booleene

O funcţie f: Bⁿ ® B, unde B = {0,1} se numeşte funcţie booleană. Această funcţie booleană y = f(x₁, x₂,…,x_n) are drept caracteristică faptul că atât variabilele cât şi funcţia nu pot lua decât două valori distincte, 0 sau 1. Funcţia va pune în corespondenţă fiecărui element al produsului cartezian n dimensional, valorile 0 sau 1. Astfel de funcţii sunt utilizate pentru caracterizarea funcţionării unor dispozitive (circuite) construite cu elemente de circuit având două stări (ex.: un întrerupător închis sau deschis, un tranzistor blocat sau în conducţie; funcţionarea unui astfel de circuit va fi descrisă de o variabilă booleană x_i).

1.4.1. Funcţii booleene elementare

Revenim la forma generală a unei funcţii booleene de n variabile:

y = f(x₁, x₂,…,x_n)

Domeniul de definiţie este format din m = 2ⁿ puncte. Deoarece în fiecare din aceste puncte funcţia poate lua doar valorile 0 şi 1 rezultă că numărul total al funcţiilor booleene de n variabile este N = 2^m.

Vom considera în continuare funcţiile elementare de 1 variabilă. Pentru n = 1 avem m = 2 şi N = 4. Funcţia are forma y = f(x) şi cele 4 forme ale ei se găsesc în tabelul următor:

fi x	0	1	Reprezentare	Denumire
f0	0	0	0	Constanta 0
f1	0	1	x	Variabila x
f2	1	0	x	Negaţia lui x
f3	1	1	1	Constanta 1

La fel se pot realiza toate funcţiile cu ajutorul unor funcţii de bază. Acestora le vor corespunde şi nişte circuite logice elementare, cu ajutorul cărora se poate realiza practic orice tip de circuit. Ţinând cont de faptul că circuitele logice de comutaţie au 2 stări stabile LOW (L) şi HIGH (H), asignând lui L ¬ 0 şi lui H ¬ 1 se poate întocmi un tabel al funcţiilor elementare.

Denumire	Funcţie	Simbol	Tabel de adevăr	Tabel de definiţie
Inversor – NOT	f = x	x f = x	x f 0 1 1 0	x f L H H L
Poartă SI – AND	f = x1 × x2	x1 x2 f=x1×x2	x1 x2 f 0 0 0 0 1 0 1 0 0 1 1 1	x1 x2 f L L L L H L H L L H H H
Poartă SAU – OR	f = x1 + x2	x1 x2 f=x1+x2	x1 x2 f 0 0 0 0 1 1 1 0 1 1 1 1	x1 x2 f L L L L H H H L H H H H
Poartă SI-NU – NAND	f = x1 × x2	x1 x2 f=x1×x2	x1 x2 f 0 0 1 0 1 1 1 0 1 1 1 0	x1 x2 f L L H L H H H L H H H L
Poartă SAU-NU – NOR	f = x1 + x2	x1 x2 f=x1+x2	x1 x2 f 0 0 1 0 1 0 1 0 0 1 1 0	x1 x2 f L L H L H L H L L H H L
SAU EXCLUSIV – XOR	f = x1 + x2	x1 x2 f=x1 + x2	x1 x2 f 0 0 0 0 1 1 1 0 1 1 1 0	x1 x2 f L L L L H H H L H H H L
COINCIDENŢĂ	f = x1 × x2	x1 x2 f=x1 × x2 =x1 + x2	x1 x2 f 0 0 1 0 1 0 1 0 0 1 1 1	x1 x2 f L L H L H L H L L H H H

1.4.2. Reprezentarea funcţiilor booleene

Există două moduri de reprezentare a funcţiilor booleene: grafică şi analitică.

1. Modalităţi grafice - se caracterizează printr-o reprezentare intuitivă, uşor de reţinut, dar sunt inadecvate pentru funcţii booleene cu un număr de variabile mai mare decât 4;

2. Modalităţi analitice - sunt mai greoaie, dar permit metode automate, deci algoritmi de simplificare a funcţiei; se folosesc în general pentru funcţii booleene cu numărul variabilelor mai mare decât 5.

1.4.2.1. Modalităţi de reprezentare grafică

Modalităţile de reprezentare grafică sunt: tabel de adevăr, diagramă Karnaugh, schemă logică, diagramă de timp.

1. Tabel de adevăr – se marchează într-un tabel corespondenţa dintre valorile de adevăr ale variabilelor de intrare şi valoarea de adevăr a funcţiei, în fiecare punct al domeniului de definiţie.

Pentru o funcţie cu n variabile de intrare vom avea 2ⁿ combinaţii.

Există situaţii în care, pentru anumite combinaţii ale variabilelor de intrare, valoarea funcţiei nu este specificată. Aceste funcţii se numesc incomplet definite. În tabel, în locul în care funcţia nu este specificată, se notează cu “X”. Dacă o funcţie booleană este incomplet definită pentru “m” combinaţii ale variabilelor de intrare se pot defini 2^m funcţii noi prin alegerea arbitrară a valorilor incomplet definite.

2. Diagramă Karnaugh

O diagramă Karnaugh pentru o funcţie booleană de n variabile se desenează sub forma unui pătrat sau dreptunghi împărţit în 2ⁿ compartimente. Fiecare compartiment este rezervat unui termen canonic al funcţiei, respectiv unuia dintre vârfurile cubului n dimensional din reprezentarea geometrică a funcţiei (2n n-uple ale funcţiei).

Diagrama Karnaugh este organizată astfel încât două compartimente vecine pe o linie sau pe o coloană corespund la doi termeni canonici care diferă numai printr-o singură variabilă, care apare în unul adevărată, iar în celălalt negată (la două n-pluri adiacente). Se consideră vecine şi compartimentele aflate la capetele opuse ale unei linii, respectiv coloane.

Diagrama Karnaugh se notează fie indicând domeniul fiecărei variabile, fie indicând pe linie şi coloană n-uple de zerouri şi unităţi corespondente unui compartiment din diagramă şi ordinea variabilelor. Prima notaţie se foloseşte în cazul în care se reprezintă funcţia prin forma ei canonică sau normală. A doua notaţie se foloseşte în cazul în care funcţia se reprezintă prin tabel de adevăr. Pentru a putea reprezenta uşor funcţii exprimate în mod convenţional prin indicii termenilor canonici se poate nota fiecare compartiment cu indicele termenului corespondent, ţinând cont de o anumită ordine a variabilelor.

Exemple:

1) Diagrama Karnaugh pentru funcţia de 2 variabile:

f(x₁, x₂) = x₁×x₂ + x₁×x₂

	x2 x1	0	1	x2 x1	0	1
	0	x1x2	x1x2	0	0	1
x2	1	x1x2	x1x2	1	1	0

x₁

sau

x₁

00

01

11

10

x₂

Obs. Numerotarea liniilor şi coloanelor se face în cod Gray (cod binar reflectat)

Cod binar direct	Cod Gray
0000	0000
0001	0001
0010	0011
0011	0010
0100	0110
0101	0111
0110	0101
0111	0100
1000	1100
1001	1101
1010	1111
1011	1110
1100	1010
1101	1011
1110	1001
1111	1000

2) Diagrama Karnaugh pentru funcţia de 3 variabile:

y = f(x₁,x₂,x₃)

Domeniul de definiţie este format din 2³ = 8 puncte şi reprezintă vârfurile unui cub cu latura 1:

x₁

001 101

011 111

000 100 x₃

010 110

x₂

Diagramele Karnaugh corespunzătoare pot fi reprezentate astfel:

x₂

	x1 x2x3	00	01	11	10
	0	^0	^1	^3	^2
x1	1	^4	^5	^7	^6

x₃

sau

			x3
	x1x2 x3	0	1
	00	^0	^1
	01	^2	^3	x2
x1	11	^6	^7
	10	^4	^5

3) Diagrama Karnaugh pentru funcţia de 4 variabile:

y = f(x₁,x₂,x₃,x₄)

			x4
	x1x2 x3x4	00	01	11	10
	00	^0	^1	^3	^2
	01	^4	^5	^7	^6	x2
x1	11	^12	^13	^15	^14
	10	^8	^9	^11	^10

x₃

Prin săgeţi am marcat vecinătăţile punctului de coordonate 0010.

4) Diagramele Karnaugh pentru funcţii de mai mult de 4 variabile se construiesc din diagrame de 4 variabile considerate ca diagrame elementare.

3. Schemă logică – reprezentare cu ajutorul simbolurilor circuitelor logice.

4. Diagramă de timp – reprezentare utilă pentru studiul unor forme tranzitorii de hazard în circuitele logice. Se reprezintă funcţii logice în a căror evoluţie intervine timpul.

Exemplu: f = x₁×x₂

x₁

x₂

f

Curs 2

1.4.2.2. Modalităţi de reprezentare analitică

1) Formele canonice

Fie o funcţie booleană f(x), unde x = (x₁,x₂,…,x_n). Se defineşte numărul i = x₁×2⁰ + x₂×2¹ + … + x_n×2^n-1 ca număr de combinaţii.

Exemplu:

x₁ x₂ x₃ f

0 0 0

0 0 1

0 1 0 ® i = 0×2² + 1×2¹ + 0×2⁰ = 2

0 1 1

Fie funcţia P_i definită pe Bⁿ ® B, deci P_i : Bⁿ ® B

P_i(x₁,x₂,…,x_n) = 1 dacă numărul de combinaţii este i

0 în caz contrar

Această funcţie se numeşte constituent al unităţii. Se poate arăta că orice funcţie booleană dată prin tabelul de adevăr se poate scrie ca o sumă de constituenţi ai unităţii.

f(x₁, x₂,…,x_n) = Pi₁ + Pi₂ + … + Pi_p = S Pi_j

i,jÎM₁

unde M₁ = mulţimea tuturor combinaţiilor argumentelor pentru care funcţia ia valoarea 1. Această formă de scriere se numeşte forma canonică disjunctivă FCD, iar termenii constituenţi se numesc termeni canonici conjunctivi sau mintermi (se mai numeşte şi forma sumă de produse).

Funcţia booleană se mai poate scrie şi sub forma S_i : Bⁿ ® B unde B = {0,1}.

S_i(x₁,x₂,…,x_n) = 0 dacă numărul de combinaţii este i

1 în caz contrar

Se poate demonstra că orice funcţie booleană poate fi adusă la forma:

f(x₁, x₂,…,x_n) = Si₁ × Si₂ × … × Si_q = P Si_j

i,jÎM₀

unde M₀ = mulţimea tuturor combinaţiilor argumentelor pentru care funcţia ia valoarea 0. Această formă de scriere se numeşte forma canonică conjunctivă FCC, iar factorii constituenţi se numesc termeni canonici conjunctivi sau maxtermi (se mai numeşte şi forma produs de sume).

Se poate demonstra că S_i = P_i.

Algoritmi de obţinere a formelor canonice pe baza tabelului de adevăr sau a diagramei Karnaugh:

FCD

- se determină toate combinaţiile variabilelor pentru care valoarea funcţiei este 1;

- se scriu mintermii corespunzători (o variabilă apare nenegată dacă are valoarea 1 şi negată dacă are valoarea 0);

- se însumează mintermii obţinuţi anterior.

FCC

- se determină toate combinaţiile variabilelor pentru care valoarea funcţiei este 0;

- se scriu maxtermii corespunzători prin însumarea variabilelor (o variabilă apare nenegată dacă are valoarea 0 şi negată dacă are valoarea 1);

- se înmulţesc maxtermii obţinuţi anterior.

Exemplu:

x₁ x₂ x₃ f

0 0 0 0

0 0 1 1 mintermul este x₁×x₂×x₃

0 1 0 0 maxtermi sunt (x₁+x₂+x₃)×(x₁+x₂+x₃)

Trecerea dintr-o formă canonică în alta se poate face în două moduri:

- cu ajutorul tabelului de adevăr;

- prin aplicarea dublei negaţii şi a teoremelor lui De Morgan.

Teorema lui Shannon

Complementul unei funcţii booleene se obţine prin complementarea fiecărei variabile şi interschimbarea operatorilor ŞI cu SAU şi reciproc.

f(x₁,x₂,…,x_n)_+,× = f(x₁,x₂,…,x_n)_×,+

Teorema de expansiune

Fie funcţia booleană f(x₁,x₂,…, x_i-1, x_i, x_i+1,…,x_n) care se expandează după variabila x_i. Avem atunci:

f(x₁,x₂,…, x_i-1, x_i, x_i+1,…,x_n) = x_i×f(x₁,x₂,…, x_i-1, 1, x_i+1,…,x_n) + x_i×f(x₁,x₂,…, x_i-1, 0, x_i+1,…,x_n)

Funcţia duală este:

f = [x_i + f(x₁,x₂,…, x_i-1, 0, x_i+1,…,x_n)]×[x_i + f(x₁,x₂,…, x_i-1, 1, x_i+1,…,x_n)]

2) Forma elementară

La formele canonice ale funcţiilor booleene termenii conţin toate variabilele independente de intrare, negate sau nenegate. Termenii formei elementare nu conţin toate variabilele de intrare. Această formă se obţine din formele canonice prin minimizare.

3) Forma neelementară

Forma neelementară conţine variabile sau grupuri de variabile comune mai multor termeni. Se obţine din celelalte forme prin aplicarea algebrei booleene. Este folosită la implementarea funcţiilor logice deoarece permite reducerea numărului de intrări în circuitele logice. Are dezavantajul măririi numărului de nivele logice.

1.4.3. Minimizarea funcţiilor booleene

Algebra booleană se foloseşte la analiza şi sinteza dispozitivelor numerice (circuite de comutaţie). Între gradul de complexitate al circuitului şi cel al funcţiei care îl descrie există o legătură directă. Aceasta este motivaţia pentru care, în etapa de sinteză a circuitelor de comutaţie, după definirea acestora, urmează în mod obligatoriu etapa de minimizare a funcţiei, având drept scop obţinerea unor forme echivalente mai simple (forma minimă).

Soluţia minimă obţinută în urma minimizării ar trebui să fie cea mai avantajoasă (economie de porţi logice, obţinerea unei scheme mai fiabile, mai ieftine). În realitate nu este întotdeauna aşa. De exemplu, dorinţa de a obţine un sistem uşor depanabil poate duce la obţinerea unei soluţii neminimale, dar care prezintă proprietăţi interesante de simetrie şi regularitate.

Prin aplicarea metodelor de minimizare (de simplificare) se ajunge la expresii minimale sub forma unor SAU-uri de SI-uri (reuniune minimală) ori a unor SI-uri de SAU-uri (intersecţie minimală).

Criteriile utilizate în vederea minimizării sunt:

- reducerea numărului de variabile;

- reducerea numărului de termeni;

- reducerea pe ansamblu a variabilelor şi termenilor, astfel ca suma lor să devină minimă.

Minimizarea constă în principal în transformarea formelor canonice şi a formelor elementare parţial simplificate în forme elementare minimale.

Metodele de minimizare pot fi grupate în metode algebrice şi metode grafice.

1.4.3.1. Minimizarea grafică

1. Diagrama Karnaugh

Minimizarea se bazează pe proprietatea de adiacenţă a codului binar reflectat (Gray) cu ajutorul căruia se numerotează liniile şi coloanele diagramei Karnaugh. În vederea minimizării se aleg suprafeţele maxime (subcuburi) formate din constituenţi ai unităţii, respectiv din constituenţi ai lui 0, suprafeţe (subcuburi) având ca dimensiune un număr de pătrate (compartimente) egal întotdeauna cu puteri ale lui 2. Aceste suprafeţe vor corespunde termenilor canonici, termenii vecini fiind adiacenţi (diferă printr-un singur bit). Ca urmare, în urma grupării lor se vor reduce variabilele pe baza relaţiei: x₁×x₂ + x₁×x₂ = x₁.

Metoda de minimizare:

- se realizează grupări de compartimente (subcuburi) care sunt puteri ale lui 2. Un compartiment poate fi membru al mai multor suprafeţe. O suprafaţă cu 2^m celule vecine va elimina 2^m variabile de intrare.

- se scriu ecuaţiile corespunzătoare fiecărei suprafeţe, obţinându-se astfel termenii elementari.

- se realizează forma disjunctivă minimă (FDM) prin însumarea termenilor elementari obţinuţi prin gruparea constituenţilor lui 1 sau forma conjunctivă minimă (FCM) prin înmulţirea termenilor elementari obţinuţi prin gruparea de constituenţi ai lui 0; funcţiile minimale obţinute sunt identice, ele diferind numai prin forma de prezentare.

Pentru a se obţine forma minimală a unei funcţii booleene este util să se minimizeze ambele forme canonice, FCC şi FCD. Apoi, în funcţie de disponibilitatea componentelor şi de numărul de conexiuni care rezultă, se poate alege forma minimală a funcţiei booleene care va fi implementată.

Exemplu:

f(x₁,x₂,x₃,x₄) = S (3, 7, 8, 9, 12, 13, 15)

			x4
	x1x2 x3x4	00	01	11	10
	00	0	0	1	0
	01	0	0	1	0	x2
x1	11	1	1	1	0
	10	1	1	0	0

x₃

Pentru FDM a funcţiei se obţin două variante, după cum se aleg suprafeţele pentru minimizare:

f_FDM1 = x₁×x₃ + x₁×x₃×x₄ + x₁×x₂×x₄ sau

f_FDM2 = x₁×x₃ + x₁×x₃×x₄ + x₂×x₃×x₄

Implementarea cu porţi de tip SI-NU arată astfel:

f_FDM1 = x₁×x₃ + x₁×x₃×x₄ + x₁×x₂×x₄ = = x₁×x₃ × x₁×x₃×x₄ × x₁×x₂×x₄

Minimizarea funcţiei negate va fi:

f_FDM = x₁×x₃ + x₃×x₄ + x₁×x₂×x₃

La fel se procedează şi la minimizarea funcţiei prin folosirea constituenţilor de 0:

			x4
	x1x2 x3x4	00	01	11	10
	00	0	0	1	0
	01	0	0	1	0	x2
x1	11	1	1	1	0
	10	1	1	0	0

x₃

Forma minimizată conjunctivă a funcţiei FCM este:

f_FCM = (x₁+x₃)×(x₃+x₄)×(x₁+x₂+x₃)

2. Diagrame Karnaugh pentru funcţii incomplet definite

Funcţiile incomplet definite sunt cele care în anumite puncte ale domeniului de definiţie pot lua valoarea 0 sau valoarea 1. Avem două posibilităţi:

- combinaţii de intrare pentru care funcţia are valori indiferente (nedefinite);

- combinaţii ale variabilelor care nu pot să apară din punct de vedere fizic; în aceste situaţii trebuie studiat dacă combinaţiile sunt susceptibile să se producă în urma unei manevre false sau în urma unui defect de funcţionare; pentru a evita funcţionarea greşită, în locaţiile corespunzătoare se impun valori pentru funcţie, astfel încât să nu se perturbe funcţionarea normală.

Valorile nespecificate precum şi locaţiile corespunzătoare din diagrama Karnaugh se numesc “indiferente” sau “arbitrare” sau “redundante”. Ele se notează cu “x” şi vor fi considerate în timpul minimizării ca având valoarea 1 sau 0, în funcţie de situaţie, pentru a se obţine o minimizare cât mai bună.

			x4
	x1x2 x3x4	00	01	11	10
	00		x	1
	01	x	1		x	x2
x1	11	1	1	1
	10	1	x	1	x

x₃

Ca să minimizăm funcţia în FDM considerăm că x au valoarea 1 şi grupăm aceşti x numai cu valorile de 1, nu şi între ei (o grupare între ei nu are nici o semnificaţie).

Se obţine: f_FDM = x₁×x₂ + x₂×x₃ + x₁×x₄ + x₂×x₄

Obs. În cazul funcţiilor incomplet definite, funcţia complementară simplificată prin grupări de 0 nu coincide întotdeauna cu complementul funcţiei.

3. Diagrame Karnaugh cu expresii

a. Superpoziţia funcţiilor booleene

Fie o funcţie booleană f(X) cu X = (x₁,x₂,…, x_i, x_i+1,…,x_n). Dacă considerăm X₁ = (x₁,x₂,…, x_i) şi X₂ = (x_i+1,…,x_n) şi dacă funcţia f(X) poate fi scrisă ca o funcţie f(X) = f₃[f₁(X₁), f₂(X₂)] atunci spunem că f(X) a fost obţinută prin superpoziţia funcţiilor f₁(X₁) şi f₂(X₂).

Dacă X₁ÇX₂ = F atunci avem o superpoziţie disjunctă, iar dacă X₁ÇX₂ ¹ F avem o superpoziţie nedisjunctă.

x₁

f

x_n

După superpoziţie avem:

x₁

f₁

x_i

f₃ f

x_i+1

f₂

x_n

b. Decompoziţia funcţiilor booleene

Dacă se dă o funcţie booleană şi un set de funcţii se cere să se realizeze o “spargere” a funcţiei booleene. S-a reuşit decompoziţia funcţiei booleene dacă:

f = f_m [f_m-1(X_m-1), f_m-2(X_m-2),…,f₁(X₁),X₀] unde X_i Ì X

Dacă f poate fi scrisă ca f = f₂[f₁(X₁),X₀] decompoziţia este simplă.

_m-1

Decompoziţia este nedisjunctă dacă: ÇXi = F

^i=j

_m-1

Decompoziţia este disjunctă dacă: ÇXi ¹ F

^i=j

Exemplu:

f(x₁,x₂,x₃,x₄) = S(0, 2, 3, 7, 9, 10, 11, 14)

			x4
	x1x2 x3x4	00	01	11	10
	00	1		1	1
	01			1		x2
x1	11				1
	10		1	1	1

x₃

f_FDM = x₁×x₂×x₄ + x₁×x₃×x₄ + x₁×x₃×x₄ + x₁×x₂×x₄ = x₂(x₁ × x₄) + x₃(x₁ + x₄) =

= x₂×G + x₃×G unde G = x₁ + x₄ şi deci f se poate scrie:

f = f₂[G(x₁,x₄), x₂,x₃]

Pornind de la această formă pentru f, facem o minimizare.

f = x₂×G + x₃×G = x₂×G×(x₃ + x₃) + x₃×G×(x₂ + x₂) =

= x₂x₃G + x₂x₃G + x₂x₃G + x₂x₃G = x₂x₃ + x₂x₃G + x₂x₃G

Diagrama Karnaugh corespunzătoare este:

	x2 x3	0	1
	0	G	1
x2	1	0	G
			x3

În general o diagramă Karnaugh cu “n” expresii (sau variabile) are 2ⁿ locaţii. Prin înglobarea în diagramă a “m” expresii (variabile) dimensiunea diagramei se reduce, numărul de locaţii devenind 2^n-m.

Pentru a minimiza o funcţie prin diagrame Karnaugh cu expresii se fac următorii paşi:

1) se consideră toate variabilele din diagramă ca şi cum ar fi 0 şi se formează suprafeţe (subcuburi) cu constituenţii lui 1;

2) se consideră toate locaţiile cu 1 indiferente şi se formează suprafeţe (subcuburi) cu variabilele înglobate;

3) se consideră intersecţia variabilelor înglobate cu grupările obţinute în pasul 2;

4) se face reuniunea termenilor din paşii 1 şi 3;

5) pentru mai mult de o variabilă înglobată se tratează pe rând conform paşilor 1 - 4 numai câte o variabilă, celelalte fiind considerate 0, iar apoi se scrie reuniunea tuturor termenilor obţinuţi.

Exemplu:

Să se minimizeze funcţia cu variabile înglobate:

x1 x2x3	00	01	11	10
0		a+b	1	c
1	1		1	x

Pasul 1.

x1 x2x3	00	01	11	10
0			1
1	1		1	x

Se obţine x₂×x₃ + x₁×x₃

Pasul 2 şi 3.

x1 x2x3	00	01	11	10
0		a+b	x	c
1	x		x	x

Se obţine c×x₂ + (a+b)×x₁×x₃

Pasul 4. f = x₂×x₃ + x₁×x₃ + c×x₂ + (a+b)×x₁×x₃

Curs 3

1.4.3.2. Minimizarea algebrică

Minimizarea algebrică a funcţiilor booleene se face cu ajutorul teoremelor algebrei booleene.

În cazul în care numărul de variabile este mai mare decât 6 se utilizează metoda de minimizare Quine-Mc Cluskey. Această metodă are avantajul că algoritmul este uşor de implementat pe calculator. Pentru prezentarea metodei vom lua ca exemplu funcţia:

f = S (0, 2, 3, 5, 7, 8, 10, 11, 13, 15)

Etapele de minimizare sunt:

1. Se grupează termenii canonici astfel încât termenii din fiecare grupă să conţină acelaşi număr de 1, respectiv 0.

TC x₁ x₂ x₃ x₄

0 0 0 0 0

2 0 0 1 0

8 1 0 0 0

3 0 0 1 1

5 0 1 0 1

10 1 0 1 0

7 0 1 1 1

11 1 0 1 1

13 1 1 0 1

15 1 1 1 1

2. Se compară fiecare termen dintr-o grupă cu toţi cei din grupa următoare, aplicând relaţia de reducere: x₁×x₂ + x₁×x₂ = x₁. Se grupează termenii care diferă printr-o singură variabilă (o singură poziţie binară). Termenul obţinut prin combinare va conţine pe poziţia respectivă semnul -.

Comparare Rezultatul comparării

între x₁ x₂ x₃ x₄

0, 2 0 0 - 0

0, 8 - 0 0 0

2, 3 0 0 1 -

2, 10 - 0 1 0

8, 10 1 0 - 0

3, 7 0 - 1 1

3, 11 - 0 1 1

5, 7 0 1 - 1

5, 13 - 1 0 1

10, 11 1 0 1 -

7, 15 - 1 1 1

11, 15 1 - 1 1

13, 15 1 1 - 1

În continuare se repetă procedeul de comparare până când nu mai este posibilă nici o reducere.

Comparare Rezultatul comparării

între x₁ x₂ x₃ x₄

0, 2, 8, 10 - 0 - 0

2, 3, 10, 11 - 0 1 -

3, 7, 11, 15 - - 1 1

5, 7, 13, 15 - 1 - 1

Termenii rezultanţi, (0, 2, 8, 10), (2, 3, 10, 11), (3, 7, 11, 15) şi (5, 7, 13, 15) se numesc implicanţi primi IP.

3. Se aleg acei implicanţi primi IP care asigură acoperirea minimală a termenilor canonici TC. Pentru aceasta se construieşte un tabel de acoperire, în care pe coloane se notează termenii canonici TC, iar pe linii implicanţii primi IP. În intersecţii se notează acei termeni canonici TC acoperiţi de fiecare implicant prim IP.

IP TC	0 2 3 5 7 8 10 11 13 15
0, 2, 8, 10	x x x x
2, 3, 10, 11	x x x x
3, 7, 11, 15	x x x x
5, 7, 13, 15	x x x x

Unii dintre implicanţii primi sunt implicanţi primi esenţiali pentru că acoperă cel puţin un termen canonic al funcţiei, care nu este acoperit de alt implicant prim. Implicanţii primi esenţiali vor face parte în mod obligatoriu din expresia minimizată a funcţiei. În cazul nostru implicanţi primi esenţiali sunt (0, 2, 8, 10) şi (5, 7, 13, 15). Pentru termenii canonici care au rămas neacoperiţi, 3 şi 11, se observă că pot fi aleşi 2 implicanţi primi, (2, 3, 10, 11) şi (3, 7, 11, 15), deci există 2 soluţii de minimizare.

f = (0, 2, 8, 10) + (5, 7, 13, 15) + (2, 3, 10, 11) = x₂x₄ + x₂x₄ + x₂x₃ şi

f = (0, 2, 8, 10) + (5, 7, 13, 15) + (3, 7, 11, 15) = x₂x₄ + x₂x₄ + x₃x₄

1.4.4. Minimizarea sistemelor de funcţii booleene

Sistemele de funcţii booleene sunt exprimate prin f: Bⁿ ® B^m unde B ={0, 1}. Argumentele pot fi de n variabile şi sunt mai multe funcţii de acest tip: f₁, f₂,…, f_m.

Pentru a minimiza sistemele de funcţii se caută implicanţi primi pentru f₁, f₂,…, f_m şi pentru produsele f₁×f₂, f₁×f₃…, f₁×f_m, … f₁×f₂×f₃,…, f₁×f₂×f₃×f₄,…, … f₁×f₂×…×f_m. Soluţia aleasă pentru implementarea sistemului de funcţii booleene va fi cea care va fi cea mai avantajoasă din punct de vedere al circuitelor disponibile şi al preţului.

Exemplu:

f₁(x₁,x₂,x₃) = S (1, 5, 6, 7)

f₂(x₁,x₂,x₃) = S (1, 4, 5, 6)

f₃(x₁,x₂,x₃) = S (0, 2, 5, 6, 7)

1. Calculăm funcţiile produs:

f₁×f₂ = S (1, 5, 6)

f₁×f₃ = S (5, 6, 7)

f₂×f₃ = S (5, 6)

f₁×f₂×f₃ = S (5, 6), identică cu f₂×f₃

2. Determinăm implicanţii primi din funcţiile simple şi din produsele determinate la punctul 1. Pentru determinarea implicanţilor primi se folosesc diagrame Karnaugh în care se iau toate acoperirile posibile.

Pentru f₁:

x1 x2x3	00	01	11	10
0		1
1		1	1	1

Pentru f₂:

x1 x2x3	00	01	11	10
0		1
1	1	1		1

Pentru f₃:

x1 x2x3	00	01	11	10
0	1			1
1		1	1	1

Pentru f₁×f₂:

x1 x2x3	00	01	11	10
0		1
1		1		1

Pentru f₁×f₃:

x1 x2x3	00	01	11	10
0
1		1	1	1

Pentru f₂×f₃ şi f₁×f₂×f₃:

x1 x2x3	00	01	11	10
0
1		1		1

3. Construim un tabel în care capetele de linii vor reprezenta funcţiile, iar coloanele vor fi implicanţii primi.

Funcţia	Implicanţi primi
	Indici	Expresii	Notaţii
f1	1,5 6,7 5,7	x2x3 x1x2 x1x3	- - -
f2	1,5 4,5 4,6	x2x3 x1x2 x1x3	- i h
f3	0,2 2,6 6,7 5,7	x1x3 x2x3 x1x2 x1x3	g f - -
f1×f2	1,5 6	x2x3 x1x2x3	e -
f1×f3	5,7 6,7	x1x3 x1x2	d c
f2×f3 = f1×f2×f3	5 6	x1x2x3 x1x2x3	b a

4. Se notează IP pe coloana a patra din tabel începând cu ultimul, iar cei care apar dublaţi nu se mai notează.

5. Se construieşte un tabel al acoperirilor funcţiilor f₁, f₂, f₃.

Notaţii

Indicii

Funcţia de unde au rezultat

f1

f2

f3

1

5

6

7

1

4

5

6

0

2

5

6

7

a

6

f1×f2×f3

x

x

x

b

5

f1×f2×f3

x

x

x

c

6, 7

f1×f3

x

x

x

x

d

5, 7

f1×f3

x

x

x

x

e

1, 5

f1×f2

x

x

x

x

f

2, 6

f3

x

x

g

0, 2

f3

x

x

h

4, 6

f2

x

x

i

4, 5

f2

x

x

6. Determinăm acoperirile optime ale funcţiilor f₁, f₂, f₃.

A(f₁) = e,c + e,d,a = A₁ + A₂ cu e implicant prim esenţial

A(f₂) = e,h + e,i,a = B₁ + B₂ cu e implicant prim esenţial

A(f₃) = g,c,b + g,c,d, + g,f,d + g,a,d = C₁ + C₂ + C₃ + C₄ cu g implicant prim esenţial

7. Se scriu toate acoperirile posibile pentru sistemul de funcţii şi se alege acea acoperire care realizează condiţiile de preţ minim şi disponibilitate de piese. Se face tabelul pentru acoperiri:

Acoperiri	Elementele acoperirii	Număr de termeni	Cost
A1B1C1	e,c,h,g,b	5	11
A1B1C2	e,c,h,g,d	5	10
A1B1C3	e,c,h,g,f,d	6
A1B1C4	e,c,h,g,a,d	6
A1B2C1	e,c,i,a,g,b	6
A1B2C2	e,c,i,a,g,d	6
A1B2C3	e,c,i,a,g,f,d	7
A1B2C4	e,c,i,a,g,d	6
A2B1C1	e,d,a,h,g,c,b	7
A2B1C2	e,d,a,h,g,c	6
A2B1C3	e,d,a,h,g,f	6
A2B1C4	e,d,a,h,g	5	11
A2B2C1	e,d,a,i,g,c,b	7
A2B2C2	e,d,a,i,g,c	6
A2B2C3	e,d,a,i,g,f	6
A2B2C4	e,d,a,i,g	5	11

Avem acoperiri minimale cu 5 termeni. Pentru a calcula costul unei acoperiri se face suma costurilor implicanţilor primi din acoperirea considerată. Costul unui implicant prim de n variabile din care lipsesc r variabile este n-r, pentru că fiecare variabilă prezentă necesită un contact, o legătură.

_n-1

C = S g_r ×(n-r)

^r=0

unde g_r este numărul subcuburilor din care lipsesc r variabile.

Pentru acoperirea A₁B₁C₂, care are elementele e,c,h,g,d, avem costul:

₂

C = S g_r ×(3-r) = g₀×3 + g₁×2 + g₂×1 = 0×3 + 5×2 + 0×1 = 10

^r=0

e = x₂x₃

c = x₁x₂

h = x₁x₃

g = x₁x₃

d = x₁x₃

Minimizarea sistemului de funcţii va fi:

f₁ = x₂x₃ + x₁x₂

f₂ = x₂x₃ + x₁x₃

f₃ = x₁x₃ + x₁x₃ + x₁x₂ = x₁x₂ + x₁ + x₃

Datorită reducerii corelate a sistemului de funcţii apar porţi comune mai multor funcţii.

Curs 4

CAPITOLUL II

CIRCUITE LOGICE COMBINAŢIONALE

2.1. Definiţii

Circuitele logice combinaţionale, CLC, sunt un caz particular al sistemelor secvenţiale finite sau al automatelor finite, numite automate de grad 0.

Circuitele logice combinaţionale se caracterizează prin faptul că variabilele de ieşire sunt independente de timp şi de starea internă, fiind determinate numai de variabilele de intrare (starea variabilelor de intrare la momentul considerat).

Legătura dintre starea ieşirii şi starea intrării unui CLC este realizată de funcţia de transfer.

x₁ y₁

x₂ y₂

CLC

x_n y_m

Oricare funcţie de ieşire y (y₁, y₂,…, y_m) este funcţie de toate variabilele de intrare (x₁, x₂,…, x_n). Un CLC se poate descrie astfel:

y₁ = f₁(x₁, x₂,…, x_n)

y₂ = f₂(x₁, x₂,…, x_n)

y_m = f_m(x₁, x₂,…, x_n)

Funcţiile se vor exprima în forma canonică disjunctivă FCD sau în forma canonică conjunctivă FCC.

Independenţa faţă de timp presupune că o dată cu modificarea variabilelor de intrare se modifică simultan şi variabilele de ieşire. Din punct de vedere practic, datorită întârzierilor produse de circuitele logice şi de conexiuni, modificarea simultană nu este posibilă. Ca urmare, pe durata procesului tranzitoriu de stabilire a variabilelor de ieşire, vectorul ieşirilor poate lua valori intermediare diferite de valoarea finală, ceea ce conduce la fenomenul de hazard combinaţional, de care trebuie să se ţină cont la proiectarea unui sistem numeric.

În general, la circuitele logice combinaţionale, vom face abstracţie de proprietăţile fizice ale porţilor logice, de faptul că un impuls teoretic diferă de unul real. Vom analiza aceste fenomene doar în cazul hazardului combinaţional.

2.2. Analiza circuitelor logice combinaţionale

În cadrul analizei CLC se pleacă de la cunoaşterea schemei logice a circuitului şi se urmăreşte stabilirea funcţionării acestuia. Stabilirea expresiei variabilei de ieşire se face de la intrare la ieşire, urmărind transformările variabilelor de intrare.

Definim ca număr de nivele al unui CLC numărul maxim de porţi dintre intrări şi ieşiri. Numerotarea nivelelor se face de la ieşire înspre intrare.

x₅

x₁

x₂

y₁

x₃

x₄ y₂

x₆ x₇

4 3 2 1

Circuitul logic combinaţional din exemplu are 4 nivele.

Există şi următoarea situaţie de legături între porţi:

x₁ y

x₂

x₃

Acest circuit are şi legături inverse. Ultimele porţi nu pot fi numerotate, deci circuitul nu este un CLC.

În CLC sunt admise legăturile inverse (ieşirea unei porţi dintr-un nivel inferior să fie dusă la intrarea unei porţi dintr-un nivel superior) cu condiţia ca definiţia CLC să fie respectată.

Algoritm de determinare a legăturilor inverse în CLC

a. Se numerotează toate porţile logice care au ca intrări un subset din mulţimea variabilelor de intrare ale circuitului logic (de la 1 la k);

b. Se numerotează de la k+1 porţile care au ca intrări fie intrări ale circuitului, fie ieşiri ale porţilor numerotate la punctul a. Dacă am reuşit să numerotăm toate porţile circuitului logic, acesta este fără legături inverse şi este circuit combinaţional. Dacă nu am reuşit numerotarea tuturor porţilor logice, circuitul este de tip secvenţial.

2.3. Sinteza circuitelor logice combinaţionale

În cadrul sintezei circuitelor logice combinaţionale se cunoaşte funcţia pe care trebuie să o îndeplinească circuitul şi se caută să se găsească structura acestuia.

Etapele sintezei circuitelor logice combinaţionale sunt:

1. Enunţul problemei;

2. Alcătuirea tabelului de adevăr, definirea funcţiei sau funcţiilor;

3. Minimizarea funcţiei sau funcţiilor;

4. Desenarea schemei circuitului

Există mai multe metode de implementare a CLC, diferenţiate după nivelul de complexitate al circuitelor integrate folosite.

2.3.1. Sinteza CLC cu circuite integrate SSI

Circuitele integrate de tip SSI – small scale integration – au până la 50 de tranzistoare integrate pe capsulă. Dintre aceste circuite fac parte porţile logice fundamentale: SI-NU (NAND), SAU-NU (NOR), NU (NOT), SI (AND), SAU (OR), SAU-EXCLUSIV (XOR).

După parcurgerea etapelor de sinteză se face implementarea funcţiei sau funcţiilor logice cu ajutorul circuitelor integrate existente. CLC de tip SSI se folosesc mai mult pentru adaptarea la aplicaţie a circuitelor de tip MSI şi LSI standardizate, care nu satisfac cu exactitate cerinţele de proiectare. Ele vor fi utilizate acolo unde circuitele cu grad înalt de integrare nu pot fi folosite.

2.3.2. Sinteza CLC cu circuite integrate MSI

Circuitele integrate de tip MSI – medium scale integration – au până la 500 de tranzistoare integrate. Ele oferă structuri mai complexe, disponibile ca şi structuri standard.

Forma funcţiilor logice pe care dorim să le implementăm cu circuite de tip MSI trebuie să fie corelată cu circuitele disponibile. De obicei nu mai este necesară minimizarea funcţiilor.

Circuite combinaţionale uzuale (specializate)

1. Convertoare de cod

Convertoarele de cod sunt CLC care permit trecerea dintr-un cod binar în altul. La intrarea circuitului se aplică cuvintele unui cod şi la ieşire se obţine alt cod. Convertoarele de cod fac compatibilă funcţionarea a 2 sisteme în care informaţia este codificată în mod diferit.

Exemplu: Conversiile din cod Gray în cod binar-zecimal (BCD) şi invers

1) Cod Gray ® BCD

Cuvintele de cod în cele două coduri sunt:

Gray: g_n, g_n-1,…, g₀

BCD: b_n, b_n-1,…, b₀

Reguli: b_n = g_n

g3	g2	g1	g0	b3	b2	b1	b0
0	0	0	0	0	0	0	0
0	0	0	1	0	0	0	1
0	0	1	1	0	0	1	0
0	0	1	0	0	0	1	1
0	1	1	0	0	1	0	0
0	1	1	1	0	1	0	1
0	1	0	1	0	1	1	0
0	1	0	0	0	1	1	1
1	1	0	0	1	0	0	0
1	1	0	1	1	0	0	1
1	1	1	1	1	0	1	0
1	1	1	0	1	0	1	1
1	0	1	0	1	1	0	0
1	0	1	1	1	1	0	1
1	0	0	1	1	1	1	0
1	0	0	0	1	1	1	1

Se construiesc diagrame Karnaugh pentru determinarea funcţiilor minimizate pentru b₃, b₂, b₁, b₀.

Diagrama Karnaugh pentru b₃:

g3g2 g1g0	00	01	11	10
00
01
11	1	1	1	1
10	1	1	1	1

Obţinem: b₃ = g₃

Diagrama Karnaugh pentru b₂:

g3g2 g1g0	00	01	11	10
00
01	1	1	1	1
11
10	1	1	1	1

Obţinem b₂ = g₂g₃ + g₂g₃ = g₂ + g₃

Diagrama Karnaugh pentru b₁:

g3g2 g1g0	00	01	11	10
00			1	1
01	1	1
11			1	1
10	1	1

Obţinem b₁ = g₁g₂g₃ + g₁g₂g₃ + g₁g₂g₃ + g₁g₂g₃ = g₁(g₂ + g₃) + g₁(g₂ + g₃) = g₁ + g₂ + g₃

Diagrama Karnaugh pentru b₀:

g3g2 g1g0	00	01	11	10
00		1		1
01	1		1
11		1		1
10	1		1

Obţinem b₀ = g₀g₁g₂g₃ + g₀g₁g₂g₃ + g₀g₁g₂g₃ + g₀g₁g₂g₃ + g₀g₁g₂g₃ + g₀g₁g₂g₃ + g₀g₁g₂g₃ + g₀g₁g₂g₃ = g₂g₃(g₀ + g₁) + … = g₀ + g₁ + g₂ + g₃

În general:

b_n = g_n

_i

b_i = 1 dacă + S g_j = 1

^j=n-1

0 dacă nu

2) Conversia din BCD în Gray:

g_n = b_n

g_i = b_i + b_i+1

2. Codificatoare

Codificatoarele sunt CLC la care activarea unei intrări conduce la apariţia unui cuvânt de cod la ieşire.

Exemplu: Codificator din zecimal în BCD (binar codificat zecimal)

Zecimal										BCD
0	1	2	3	4	5	6	7	8	9	2^3	2^2	2^1	2^0
0	1	1	1	1	1	1	1	1	1	0	0	0	0
1	0	1	1	1	1	1	1	1	1	0	0	0	1
1	1	0	1	1	1	1	1	1	1	0	0	1	0
1	1	1	0	1	1	1	1	1	1	0	0	1	1
1	1	1	1	0	1	1	1	1	1	0	1	0	0
1	1	1	1	1	0	1	1	1	1	0	1	0	1
1	1	1	1	1	1	0	1	1	1	0	1	1	0
1	1	1	1	1	1	1	0	1	1	0	1	1	1
1	1	1	1	1	1	1	1	0	1	1	0	0	0
1	1	1	1	1	1	1	1	1	0	1	0	0	1

Intrările sunt active pe 0 logic. De exemplu, dacă este activă (adică 0) intrarea 5, pe ieşire se va obţine codul în BCD pentru 5, adică 0101.

Funcţiile pentru ieşiri sunt:

2³ = 8 × 9

2² = 4 × 5 × 6 × 7

2¹ = 2 × 3 × 6 × 7

2⁰ = 1 × 3 × 5 × 7 × 9

Codificatorul prioritar este un codificator care are mai multe intrări active simultan şi la ieşire se obţine cuvântul de cod care corespunde intrării care este cea mai prioritară. Prioritatea creşte de la cifra 0 înspre cifra 9.

3. Decodificatoare

Decodificatoarele sunt CLC la care se activează doar una dintre ieşiri, pentru combinaţia (codul) corespunzătoare a variabilelor de intrare. Ele au funcţie inversă codificatoarelor. Ieşirile decodificatoarelor sunt active pe 0 logic (funcţionează în logică negativă).

I₁ y₁

Circuite SI-NU

I_n y_m

Numărul ieşirilor distincte este m £ 2ⁿ.

Exemplu: Decodificator pentru 3 cifre binare.

I2	I1	I0	O7	O6	O5	O4	O3	O2	O1	O0
0	0	0	1	1	1	1	1	1	1	0
0	0	1	1	1	1	1	1	1	0	1
0	1	0	1	1	1	1	1	0	1	1
0	1	1	1	1	1	1	0	1	1	1
1	0	0	1	1	1	0	1	1	1	1
1	0	1	1	1	0	1	1	1	1	1
1	1	0	1	0	1	1	1	1	1	1
1	1	1	0	1	1	1	1	1	1	1

Funcţiile pentru ieşiri sunt: O₇ = I₂I₁I₀; O₆ = I₂I₁I₀; O₅ = I₂I₁I₀; O₄ = I₂I₁I₀; O₃ = I₂I₁I₀; O₂ = I₂I₁I₀; O₁ = I₂I₁I₀; O₀ = I₂I₁I₀.

4. Multiplexoare

Multiplexoarele sunt CLC care permit trecerea datelor de pe una din intrări la o ieşire unică. Selecţia intrării se face printr-un cuvânt de cod de selecţie numit şi adresă.

I₀

MUX y

I_n-1

s_m-1 s₀

Cu m linii de selecţie se pot selecta 2^m intrări. Funcţia realizată de ieşire este:

y = I_k unde k este numărul de combinaţii

k = s_m-1 × 2^m-1 + … + s₀ × 2⁰

Aplicaţiile cele mai importante ale MUX sunt la selecţia secvenţială a datelor, conversia paralel-serie a datelor, sisteme de transmisie a datelor pe un singur canal, implementarea circuitelor logice combinaţionale cu o singură ieşire.

Exemple

1) I₀

MUX y

I₁ 2 : 1

s

Multiplexorul de tip 2:1 are 2 semnale de intrare, I₀ şi I₁, un semnal de selecţie s şi o ieşire y. În funcţie de semnalul de selecţie avem pentru ieşire: y = I₀ × s + I₁ × s.

s = 0 ® y = I₀

s = 1 ® y = I₁

Deci multiplexorul lasă să treacă spre ieşire semnalul de pe acea linie de intrare corespunzătoare lui s.

2) I₀

I₁ MUX

I₂ 4 : 1 y

I₃

s₀ s₁

Multiplexorul de tip 4:1 are 4 semnale de intrare, 2 semnale de selecţie şi un semnal de ieşire. Ieşirea va fi:

y = I₀ × s₀ × s₁ + I₁ × s₀ × s₁ + I₂ × s₀ × s₁ + I₃ × s₀ × s₁

Există multiplexoare de tip 8 : 1, 16: 1, 32 : 1. Multiplexoarele integrate au disponibile atât ieşirea adevărată cât şi cea negată. Ele au şi o intrare de “Enable” pentru validare, care permite o funcţie SI suplimentară.

5. Demultiplexoare

Demultiplexoarele sunt CLC care permit transmiterea datelor de pe o intrare de date comună pe una din ieşirile selectate. Selectarea ieşirii se face cu ajutorul unui cuvânt de cod de selecţie numit şi adresă.

y₀

I DEMUX

y_n-1

s_m-1 s₀

Cu m linii de selecţie se pot selecta 2^m ieşiri. Funcţiile de ieşire sunt:

y₀ = s_m-1 × … × s₀ × I

y₁ = s_m-1 × … × s₀ × I

y₂^m = s_m-1 × … × s₀ × I

6. Comparatoare numerice

Comparatoarele numerice sunt CLC care permit determinarea valorii relative a două numere binare. Comparatoarele pot fi de 1 bit sau de mai mulţi biţi.

Exemplu: Comparator pe 1 bit

A_i y₁

y₂

B_i y₃

Funcţiile de ieşire sunt:

y₁ = A_i × B_i pentru A_i < B_i,

y₂ = A_i + B_i pentru A_i = B_i

y₃ = A_i × B_i pentru A_i > B_i

Acest circuit constituie celula de bază pentru compararea numerelor cu mai mulţi biţi.

7. Detectoare-generatoare de paritate

Detectoarele-generatoare de paritate sunt CLC cu rol de a determina şi genera paritatea sau imparitatea numărului de variabile de intrare egale cu 1. Bitul de paritate este utilizat ca metodă de verificare a transferului de date. Sunt posibile 2 situaţii:

a. numărul biţilor de 1 + bitul de paritate = număr par

b. numărul biţilor de 1 + bitul de paritate = număr impar

Realizarea detectoarelor de paritate se bazează pe funcţia logică SAU-EXCLUSIV (0 pentru par şi 1 pentru impar).

8. Sumatoare-scăzătoare

Sumatoarele şi scăzătoarele sunt CLC care realizează adunarea, respectiv scăderea cifrelor binare.

Semisumatorul este un CLC care efectuează suma a 2 numere binare de câte 1 bit, fără a ţine cont de transportul de la bitul de semnificaţie imediat inferioară. Semisumatorul este:

A₀ S₀

1/2 S

B₀ C₀

Valorile pentru suma S₀ şi transportul spre rangul superior C₀ sunt:

S₀ = A₀ × B₀ + A₀ × B₀ = A₀ + B₀

C₀ = A₀ × B₀

Sumatorul pentru bitul de rang n este:

A_n S_n

C_n-1 S

B_n C_n

Valorile pentru suma S_n şi transportul C_n pentru rangul superior sunt:

S_n = A_n × B_n × C_n-1 + A_n × B_n × C_n-1 + A_n × B_n × C_n-1 + A_n × B_n × C_n-1 =

= (A_n + B_n) × C_n-1 + (A_n + B_n) × C_n-1 = A_n + B_n + C_n-1

C_n = A_n × C_n-1 + B_n × C_n-1 + A_n × B_n

Sumatoarele pentru cuvinte binare cu mai mulţi biţi se realizează prin interconectarea sumatoarelor pentru 1 bit. Adunarea se efectuează în paralel, iar propagarea transportului în serie.

Semiscăzătorul de 1 bit are ieşirile:

D₀ = A₀ × B₀ + A₀ × B₀ = A₀ + B₀

I₀ = A₀ × B₀

Scăzătorul complet de rangul n are ieşirile:

D_n = A_n × B_n × I_n-1 + A_n × B_n × I_n-1 + A_n × B_n × I_n-1 + A_n × B_n × I_n-1 = =(A_n + B_n) × I_n-1 + (A_n + B_n) × I_n-1 = A_n + B_n + I_n-1

I_n = A_n × I_n-1 + B_n × I_n-1 + A_n × B_n

Scăzătoarele pentru cuvinte binare cu mai mulţi biţi se realizează prin interconectarea scăzătoarelor pentru 1 bit.

9. Unităţi aritmetico-logice

Unităţile aritmetico-logice sunt CLC care realizează operaţii de tip aritmetic şi operaţii de tip logic.

Curs 5

2.3.2.1. Implementarea funcţiilor booleene cu circuite MSI

Circuitele integrate de tip MSI cum sunt decodificatorul DCD, demultiplexorul DEMUX şi multiplexorul MUX pot fi considerate circuite universale deoarece generează în interior toţi termenii canonici.

Implementarea cu DCD a unei funcţii booleene nu necesită operaţii de minimizare. La ieşirea DCD se obţin toţi termenii canonici negaţi ai formei canonice disjunctive FCD ai funcţiei. Realizarea funcţiei se face cu o poartă logică de tip SI-NU, cu un număr de intrări egal cu numărul de termeni ai funcţiei.

Implementarea cu MUX a unei funcţii booleene se bazează pe relaţia care defineşte funcţionarea sa. De exemplu, pentru un MUX de tip 4:1 avem ecuaţia ieşirii:

y = I₀ × x₁ × x₂ + I₁ × x₁ × x₂ + I₂ × x₁ × x₂ + I₃ × x₁ × x₂

în care se observă că există intrări separate pentru fiecare din cele 4 combinaţii ale variabilelor de selecţie x₁, x₂.

Dacă avem o funcţie booleană de n variabile de intrare se pot da factor variabilele x₁ şi x₂ şi se obţin 4 funcţii de n-2 variabile de intrare, care se vor conecta la intrările I₀ – I₃ ale unui MUX de tip 4:1. Similar, cu un MUX 8:1 se pot elimina 3 variabile de intrare, iar cu un MUX 16:1 se pot elimina 4 variabile de intrare.

Dacă avem o funcţie de 4 variabile se pot elimina 3 variabile prin aplicarea lor pe intrările de selecţie ale unui MUX 8:1. La cele 8 intrări ale MUX se vor conecta cele 8 funcţii de o variabilă. Singurele funcţii posibile de o variabilă sunt: x_i, x_i, 0, 1. Deci putem implementa orice funcţie cu 4 variabile de intrare folosind un singur MUX de 8 căi şi fără porţi adiţionale.

Exemplu

Considerăm funcţia: f = (0, 1, 3, 5, 9, 10, 13, 15) = x₃x₂x₁x₀ + x₃x₂x₁x₀ + x₃x₂x₁x₀ + x₃x₂x₁x₀ + x₃x₂x₁x₀ + x₃x₂x₁x₀ + x₃x₂x₁x₀ + x₃x₂x₁x₀

Folosim un MUX 8:1 şi aplicăm variabilele x₂x₁x₀ pe intrările de selecţie. Pentru a determina intrările multiplexorului, I₀ – I₇, vom face un tabel:

I₀ x₃ x₂x₁x₀

I₁ 1 (x₃ + x₃) × x₂x₁x₀

I₂ x₃ x₂x₁x₀

I₃ x₃ x₂x₁x₀

I₄ 0 x₂x₁x₀

I₅ 1 (x₃ + x₃) × x₂x₁x₀

I₆ 0 x₂x₁x₀

I₇ x₃ x₂x₁x₀

Implementarea funcţiei cu MUX este:

En

x₃

1

x₃

x₃ f

0 f

1

0

x₃ s₂ s₁ s₀

x₂ x₁ x₀

Avantajele implementării cu MUX:

- se poate implementa funcţia cu un sigur circuit de tip MUX;

- intrarea de Enable poate fi folosită ca un SI final cu întreaga funcţie;

- doar o singură variabilă trebuie să fie disponibilă şi adevărată şi negată.

Dezavantajele implementării cu MUX:

- nu se pot folosi termeni în comun în cazul minimizării sistemelor de funcţii (sisteme cu mai multe ieşiri);

- nu se poate face implementarea funcţiilor la care numărul de termeni este mai mare decât numărul intrărilor MUX;

- există multe funcţii care pot fi implementate comod prin utilizarea de porţi logice ® MUX utilizat doar pentru funcţii dificile.

Procedura de implementare cu MUX se poate face plecând de la diagrama Karnaugh. Se construieşte o diagramă Karnaugh în care se defineşte domeniul intrărilor I.

x3x2 x1x0	00	01	11	10
00	I0	I1	I3	I2
01	I4	I5	I7	I6
11	I4	I5	I7	I6
10	I0	I1	I3	I2

x3x2 x1x0	00	01	11	10
00	1	1	1
01		1
11		1	1
10		1		1

Variabila care variază este x₃. Configuraţiile de 1 din diagrama Karnaugh indică modul de conectare a intrărilor MUX, la x₃, x₃, 1 sau 0.

I₀ = x₃; I₁ = 1; I₂ = x₃; I₃ = x₃; I₄ = 0; I₅ = 1; I₆ = 0; I₇ = x₃

2.3.3. Sinteza CLC cu circuite integrate LSI

Circuitele integrate de tip LSI – Large Scale Integration – au peste 500 de tranzistoare integrate pe capsulă. Pentru exemplificarea sintezei CLC se descriu două tipuri de circuite din această categorie: ROM (Read Only Memory) şi PLA (Programmable Logic Array), cu varianta FPLA.

2.3.3.1. Sinteza CLC cu memorii de tip ROM

Memoria de tip ROM este numită şi memorie fixă sau permanentă. Ea este nevolatilă, conţinutul ei nu se modifică în timpul funcţionării. Structura ei este stabilită în procesul de fabricaţie sau este stabilită de utilizator prin programare.

I₀ O₀

DCD Matrice

I_n-1 O_m-1

Memoria ROM este formată din două niveluri de porţi logice: SI (un decodificator) şi SAU-NU (matricea de memorie). DCD din primul nivel primeşte codurile de intrare în binar (n este numărul intrărilor) şi activează pentru fiecare cod o ieşire din cele 2ⁿ. Ieşirile DCD se conectează sau nu se conectează la circuitele de tip SAU-NU şi astfel se memorează un 0 sau un 1 logic.

Vectorii de intrare în ROM se numesc adrese şi reprezintă codurile în binar ale numerelor asociate fiecărui cuvânt de memorie. Ieşirile sunt de obicei “three-state” sau “open colector” pentru a permite legarea în paralel cu ieşirile altor memorii.

Avem notaţiile:

n = numărul de biţi ai vectorului de intrare (adresa)

c = numărul de cuvinte memorate în ROM ® c = 2ⁿ

b = numărul de biţi din fiecare cuvânt

Numărul de cuvinte trebuie să fie putere a lui 2. Modul de organizare a ROM este specificat prin produsul c x b. Capacitatea memoriei se exprimă prin numărul total de biţi memoraţi: C = 2ⁿ x b. Unitatea de măsură pentru capacitatea memoriei este kilobitul (1 Kb = 1024 biţi).

Memoriile au o intrare de “Enable” care permite (E = 0) sau inhibă (E = 1) funcţionarea ROM. Dacă memoria este dezactivată, indiferent de adresare, ieşirile sunt pe semnal logic 1.

Aplicaţiile mai importante ale memoriilor de tip ROM sunt:

- memorarea instrucţiunilor şi datelor în sisteme de calcul şi automate secvenţiale;

- transformări de adresă şi înmagazinarea instrucţiunilor în microprogramare;

- conversii de cod;

- generatoare de caractere;

- generare de secvenţe de impulsuri;

- implementarea CLC cu un număr mare de variabile de intrare şi ieşire.

Implementarea CLC cu un număr mare de variabile de intrare şi ieşire se bazează pe structura internă a memoriei ROM. Pe nivelul de DCD se decodifică toţi termenii canonici. Fiecare cuvânt de la intrarea matricei reprezintă de fapt un termen canonic format din variabilele de intrare. La nivelul următor se adună toţi termenii din expresia oricărei funcţii şi rezultă funcţia de ieşire. Lista de cuvinte din ROM este chiar tabelul de adevăr al CLC. La implementarea cu ROM nu este necesară minimizarea, deoarece sunt memoraţi toţi termenii canonici şi sunt incluse toate posibilităţile de apariţie a acestora în funcţia de ieşire.

Pentru folosirea eficientă a memoriei ROM în sinteza funcţiilor booleene, variabilele de intrare şi ieşire trebuie codate, astfel încât să conţină cât mai multă informaţie. Se poate codifica orice grup de variabile care sunt mutual exclusive, adică doar una dintre ele poate fi activă la un moment dat.

Pentru reducerea numărului de intrări în ROM se utilizează des şi multiplexoarele.

Exemplu: Să se implementeze cu ROM funcţiile:

f₀(x₃,x₂,x₁,x₀) = x₃ × x₂ × x₁ × x₀

f₁(x₃,x₂,x₁,x₀) = x₂ × x₁

f₂(x₃,x₂,x₁,x₀) = x₃ × x₂ × x₁ × x₀ + x₃ × x₂ × x₀ + x₃ × x₂ × x₀ + x₂ × x₁

Memoria folosită este de tipul:

x₃ A₃

x₂ A₂ 16 x 4 biţi

x₁ A₁

x₀ A₀ CS

D₃D₂D₁D₀

f₂ f₁ f₀

Cu A s-au notat intrările de adrese, cu D datele şi cu CS (chip select), intrarea de Enable a circuitului.

Conţinutul înscris în memorie este dat în tabelul următor:

A3	A2	A1	A0	D3	f2	f1	f0
0	0	0	0	0	0	0	0
0	0	0	1	0	1	0	0
0	0	1	0	0	0	0	0
0	0	1	1	0	0	0	0
0	1	0	0	0	0	1	0
0	1	0	1	0	0	1	0
0	1	1	0	0	1	0	0
0	1	1	1	0	1	0	0
1	0	0	0	0	1	0	0
1	0	0	1	0	0	0	0
1	0	1	0	0	1	0	1
1	0	1	1	0	0	0	0
1	1	0	0	0	0	1	0
1	1	0	1	0	1	1	0
1	1	1	0	0	1	0	0
1	1	1	1	0	1	0	0

Scopurile urmărite la implementarea cu ROM sunt:

- utilizarea unui număr minim de circuite integrate;

- folosirea integrală a capacităţii memoriei.

Pentru implementarea CLC cu memorii ROM trebuie urmărite următoarele etape:

- stabilirea dimensiunii memoriei necesare pentru aplicaţia respectivă;

- alegerea tipurilor de circuite de tip ROM cu dimensiuni identice sau cât mai apropiate de cele stabilite anterior;

- dacă nu există memorii cu dimensiuni identice sau apropiate de cele dorite se fac transformări de dimensiuni (modificarea numărului de cuvinte sau numărului de biţi pe cuvânt);

- stabilirea tabelului de adevăr al ROM;

- reducerea dimensiunii ROM atunci când este posibil prin utilizarea codificării intrărilor sau ieşirilor şi a multiplexării intrărilor.

2.3.3.2. Sinteza CLC cu PLA

PLA (Programmable Logic Array) este un CLC cu două nivele de logică programabilă, o matrice de porţi SI şi o matrice de porţi SAU. PLA este de fapt o structură universală, extinsă, de implementare cu 2 nivele de porţi logice. Ambele matrici sunt programabile, în procesul de fabricaţie sau de către utilizator, conform aplicaţiei concrete. PLA este o structură mobilă şi se utilizează eficient pentru sisteme cu mai mult de 8 variabile de intrare.

Deoarece la PLA sunt programabile ambele nivele, implementarea se face pornind de la termenii elementari ai funcţiei, obţinuţi prin minimizarea ei.

Reprezentarea schematică a PLA cu n intrări, m ieşiri şi p termeni elementari realizabili este:

x₁ conexiune programabilă

x₂

x_n

Matrice

SI

1 p

1 f₁

conexiune Matrice

programabilă SAU

f_m

m

conexiune programabilă

CS

Avantajele implementării cu PLA faţă de implementarea cu ROM se referă la posibilitatea programării matricei SI şi a complementării variabilelor de ieşire (variabilele de ieşire pot fi programate individual ca active pe 0 sau pe 1).

Aplicaţii ale PLA sunt la:

- microprogramare;

- conversii de cod;

- generare de caractere;

- realizare de tabele de funcţii;

- implementarea automatelor secvenţiale.

Observaţie. Există circuite integrate cu grad şi mai mare de integrare (VLSI) utilizate în implementare. Amintim dintre acestea FPGA (Field Programmable Gate Array).

2.4. Hazardul combinaţional

Datorită întârzierilor produse de circuitele logice şi de firele de legătură ale unui CLC se poate ca starea ieşirii circuitului în momentul modificării stării variabilelor să nu coincidă cu valoarea funcţiei corespunzătoare valorii intrărilor în momentul considerat. Pentru timp scurt circuitul are o comportare greşită, numită hazard.

Exemplu

f(x₁,x₂,x₃) = x₁ × x₃ + x₂ × x₃

x₁ D₁ f’

x₃ g D₃

f

x₂ D₂

x₃ h

Diagrama Karnaugh pentru funcţie este:

x1 x2x3	00	01	11	10
0	1		1	1
1			1

În practică întârzierile D₁, D₂, D₃ ale porţilor SI-NU nu sunt egale, de aceea poate să apară hazardul combinaţional şi când se pune condiţia ca doar o singură variabilă de intrare să se modifice la un moment dat.

Hazardul apare atunci când starea intrărilor x₁x₂x₃ se modifică de la 010 la 011 sau invers.

x₁

x₂

x₃

D₁

g

D₂

h

f’

f

D₃

t_r

D₂ > D₁ deşi starea ar trebui să fie nemodificată.

După timpul de reacţie t_r = D₁ + D₂ va apare la ieşire un impuls negativ de durată Dt = D₂ - D₁ şi în această durată ieşirea ia o valoare incorectă.

Eliminarea hazardului static se poate face în cazul în care se impune ca la un moment dat să se modifice starea unei singure variabile de intrare. Pentru realizarea funcţiei se consideră şi unii termeni redundanţi din diagrama Karnaugh, astfel încât oricare doi de 1 aflaţi în căsuţe adiacente în diagramă să fie incluşi cel puţin într-un contur luat în considerare la sinteza schemei.

Pentru exemplul dat se va introduce în expresia funcţiei termenul x₁x₂.

f = x₂ × x₁ + x₃ × x₁ + x₃ × x₂

x₁ g D₁

x₃

f’

x₂ h D₂ D₃ f

x₃

x₁ i Dt

x₂

x₁

x₂

x₃

D₁

g

D₂

h

i

f’

f

Observaţii

1. Hazardul static poate să apară şi când D₁ > D₂, la schimbarea 011 în 000.

2. Proiectarea unui CLC când se schimbă mai mult decât o singură variabilă de intrare la un moment dat, fără să apară hazard, este mai dificilă sau chiar imposibil de realizat (hazard de funcţie).

3. Eliminarea sigură a hazardului se poate face luând în considerare ieşirea circuitului după un interval de timp mai mare decât întârzierea maximă din circuit.

Curs 6

CAPITOLUL III

CIRCUITE LOGICE SECVENŢIALE

Circuitele logice secvenţiale, CLS, sunt automate de ordinul 1. Se obţin din automatele de ordinul 0 (CLC) prin introducerea unor reacţii (legături inverse). Sunt alcătuite din circuite logice combinaţionale şi elemente de memorare binară.

Semnalele de ieşire ale CLS depind atât de combinaţia semnalelor aplicate pe intrări cât şi de starea circuitului. Un CLS este caracterizat printr-o secvenţă a semnalelor de ieşire şi o secvenţă a stărilor elementelor de memorie, pentru fiecare secvenţă a semnalelor aplicate pe intrările circuitului.

După modul de funcţionare (modul de transmitere a semnalelor) există 2 categorii principale de CLS:

1. asincrone – comportarea este determinată de aplicarea pe intrări a semnalelor în momente oarecare; starea circuitului depinde de ordinea în care se schimbă semnalele;

2. sincrone – comportarea este determinată de aplicarea pe intrări a semnalelor în momente discrete, bine determinate în timp; sincronizarea se realizează cu ajutorul unor impulsuri date de un generator de tact (ceas).

Exemple de CLS: bistabili, numărătoare, registre, memorii RAM.

3.1. Circuite basculante bistabile

Definiţie. Circuitele basculante bistabile (CBB sau bistabil) sunt circuite logice secvenţiale care au două stări stabile distincte. Trecerea dintr-o stare în alta se face la aplicarea unei comenzi din exterior.

Caracteristica principală a CBB este că sunt sisteme cu memorie (elemente de memorie binară). Un bistabil poate păstra un timp nedefinit informaţia binară şi în acelaşi timp starea sa poate fi citită în orice moment. Se asociază uneia dintre cele 2 stări ale bistabilului funcţia de memorare a cifrei binare 1 şi celei de a doua stări funcţia de memorare a cifrei binare 0. Bistabilul are 2 ieşiri, una care pune în evidenţă cifra binară memorată, numită ieşire adevărată şi a doua, care pune în evidenţă valoarea negată a cifrei binare memorate, denumită ieşire negată.

3.1.1. Bistabilul RS asincron (latch)

Bistabilul RS asincron are 2 intrări de comandă (de date): S (Set) şi R (Reset) şi două ieşiri Q şi Q (complementare).

Simbolul bistabilului RS asincron este:

S Q

R Q

Tabelul de adevăr al bistabilului RS asincron este:

t_n t_n+1

S_n R_n Q_t+1

0 0 Q_t

1 0 1

0 1 0

1 1 *

Din punct de vedere logic nu are sens să se facă simultan înscrierea şi ştergerea informaţiei, ca urmare S_n = 1 şi R_n = 1 va fi o situaţie interzisă (de nedeterminare, pentru că nu se poate prevedea starea finală). Condiţia de bună funcţionare care se pune este S_n × R_n = 0.

Pentru a face sinteza circuitului vom considera semnalul de ieşire Q_t+1 la momentul t_n+1, semnal care depinde de starea intrărilor S_n şi R_n şi de starea Q_t, la momentul t_n. Vom scrie Q_t+1 ca o funcţie de 3 variabile:

Q_t S_n R_n Q_t+1

0 0 0 0

0 0 1 0

0 1 0 1

0 1 1 *

1 0 0 1

1 0 1 0

1 1 0 1

1 1 1 *

Diagramele Karnaugh pentru Q_t+1 şi Q_t+1 sunt următoarele:

Q_t+1:

Qt SnRn	00	01	11	10
0	0	0	x	1
1	1	0	x	1

Q_t+1:

Qt SnRn	00	01	11	10
0	1	1	x	0
1	0	1	x	0

Dacă minimizăm funcţiile în FCC obţinem:

Q_t+1 = R_n × (S_n + Q_t)

Q_t+1 = S_n × (R_n + Q_t)

Deducem funcţiile pentru schema cu porţi de tip SAU-NU:

Q_t+1 = Q_t+1 = R_n × (S_n + Q_t) = R_n + (S_n + Q_t)

Q_t+1 = Q_t+1 = S_n × (R_n + Q_t) = S_n + (R_n + Q_t)

R Q

S Q

Schema bistabilului RS asincron realizat cu porţi de tip SI-NU se bazează pe funcţiile în forma FCD obţinute din diagramele Karnaugh:

Q_t+1 = S_n + (Q_t × R_n)

Q_t+1 = R_n + (Q_t × S_n)

Q_t+1 = S_n + (Q_t × R_n) = S_n × (Q_t × R_n)

Q_t+1 = R_n + (Q_t × S_n) = R_n × (Q_t × S_n)

S Q

R Q

Pentru S_n = R_n = 1 rezultă Q = 0 şi Q = 0, cele două ieşiri nefiind complementare. Circuitul îşi pierde în acest caz caracterul de circuit bistabil, cu două stări distincte stabile.

Bistabilul RS asincron este cel mai simplu element de memorare care poate fi realizat cu circuite logice elementare.

Observaţie. O aplicaţie tipică a bistabilului RS asincron este utilizarea acestuia la eliminarea oscilaţiilor ce apar la contactele mecanice.

3.1.2. Bistabilul RS sincron (latch cu ceas)

Bistabilul RS sincron se obţine din bistabilul RS asincron prin adăugarea unor porţi logice suplimentare cu scopul de a răspunde la semnalele de intrare R şi S numai sub acţiunea unui semnal de comandă numit impuls de tact (ceas).

S_a

S Q

CLK

R Q

R_a

Ieşirile bistabilului RS sincron se modifică doar când semnalul de tact (ceas) CLK este activ. Simbolul bistabilului RS sincron este:

S Q

CLK

R Q

Diagrama de timp pentru bistabilul RS sincron este:

CLK

R

S

Q

Funcţionarea este descrisă de funcţiile:

Q_t+1 = S + R × Q_t

Q_t+1 = R + S × Q_t

S × R = 0

Şi la acest bistabil situaţia intrărilor în care S = R = 1 introduce o nedeterminare, de aceea ea trebuie evitată.

Cât timp CLK este 0, intrările de date nu influenţează bistabilul. Când CLK = 1 bistabilul urmăreşte modificările intrărilor de date. Când CLK redevine 0 bistabilul se zăvorăşte (de aceea se numeşte latch), păstrează informaţia avută anterior pe ieşire.

Introducem noţiunea de funcţie de excitaţie, caracteristică pentru fiecare bistabil. Ea pune în evidenţă cum trebuie să fie intrările bistabilului (ce stare trebuie să aibă) pentru a se realiza o tranziţie specifică.

Tabelul de excitaţie pentru bistabilul RS sincron este:

Q_t Q_t+1 R S

0 0 x 0

0 1 0 1

1 0 1 0

1 1 0 x

Observaţie. În afara intrărilor sincrone, la bistabilul RS sincron se introduc şi intrări asincrone, R_a şi S_a, la nivelul bistabilului RS asincron (porţile SI-NU). Aceste intrări sunt utilizate cu scopul forţării la 0, prin R_a, sau la 1, prin S_a, a ieşirii bistabilului. Apariţia unor comenzi pe aceste intrări se execută independent de prezenţa sau absenţa tactului. Din acest motiv intrările asincrone ale unui bistabil sunt prioritare în raport cu intrările sincrone.

3.1.3. Bistabilul D sincron (delay)

Bistabilul D sincron are o singură intrare, D şi cele 2 ieşiri complementare, Q şi Q. Starea următoare a bistabilului D este determinată de modificarea intrării D. El întârzie cu un tact informaţia pe care o primeşte pe intrare (circuit elementar de întârziere). Sunt cele mai răspândite bistabile în registrele de date. Simbolul bistabilului D sincron:

S

D Q

CLK

Q

R

Bistabilul D se obţine din bistabilul RS sincron:

D Q

CLK

Q

Funcţiile bistabilului D sunt:

Q_t+1 = D

Q_t+1 = D

Tabelul de adevăr al bistabilului D este:

D Q

0 0

1 1

Tabelul de excitaţie al bistabilului D este:

Q_t Q_t+1 D

0 0 0

0 1 1

1 0 0

1 1 1

Starea următoare a bistabilului de tip D sincron este dependentă doar de semnalul aplicat pe intrare, ea fiind independentă de starea actuală a bistabilului.

Există două tipuri de bistabile de tip D sincron, unele care comută pe front (atunci când se schimbă tactul) şi altele care comută pe nivel (atunci când tactul este pe nivel).

3.1.4. Bistabilul JK sincron

Bistabilul JK sincron elimină situaţia de nedeterminare pe ieşiri, prezentă la bistabilul RS sincron, la combinaţia S = R = 1 pe intrări. Se folosesc reacţii (legături inverse) suplimentare.

Tabelul de adevăr al bistabilului JK sincron este:

J K Q_t+1

0 0 Q_t

0 1 0

1 0 1

1 1 Q_t

Tabelul de excitaţie al bistabilului JK sincron este:

Q_t Q_t+1 J K

0 0 0 x

0 1 1 x

1 0 x 1

1 1 x 0

Funcţiile pentru bistabilul de tip JK se determină din diagrama Karnaugh, pe baza tabelului de adevăr în forma detaliată:

Q_t J K Q_t+1

0 0 0 0

0 0 1 0

0 1 0 1

0 1 1 1

1 0 0 1

1 0 1 0

1 1 0 1

1 1 1 0

Q_t+1:

Qt JK	00	01	11	10
0			1	1
1	1			1

Q_t+1 = J × Q_t + K × Q_t

Q_t+1 = J × Q_t + K × Q_t

Un bistabil de tip JK sincron se obţine din bistabilul RS sincron prin efectuarea legăturilor care permit eliminarea condiţiei R × S = 0.

R = K × Q_t

S = J × Q_t

Q

J

CLK sau

K Q

S

J Q

CLK

K Q

R

Intrările S şi R sunt intrările asincrone, care acţionează la ultimul nivel de porţi logice, nu depind de semnalul de tact şi sunt prioritare faţă de intrările sincrone J şi K (adică în momentul în care una dintre ele se activează, bistabilul va funcţiona în regim asincron).

Simbolul utilizat pentru bistabilul JK sincron este:

S

J Q

CLK

K Q

R

O analiză mai atentă a bistabilului JK sincron arată că atât timp cât intrarea de tact (CLK) rămâne pe 1 logic după stabilirea noii stări, bistabilul intră în oscilaţie (îşi tot schimbă starea). Pentru a exista o singură comutare, durata impulsului pe CLK trebuie să fie mai mare decât timpul de propagare a semnalului printr-o poartă logică şi mai mică decât timpul de propagare a semnalului prin două porţi logice.

3.1.5. Bistabilul T sincron (Toggle)

Bistabilul T sincron se obţine din bistabilul JK sincron prin legarea intrărilor J şi K împreună. Bistabilul schimbă starea (comută) când pe intrare are semnal logic 1.

S

T Q

CLK

Q

R

Tabelul de adevăr al bistabilului T sincron este:

T Q_t+1

0 Q_t

1 Q_t

Tabelul de excitaţie al bistabilului T sincron este:

Q_t Q_t+1 T

0 0 0

0 1 1

1 0 1

1 1 0

Pentru determinarea funcţiilor bistabilului T sincron utilizăm diagrama Karnaugh de 2 variabile:

Qt T	0	1
0		1
1	1

Q_t+1 = T × Q_t + T × Q_t = T + Q_t

Q_t+1 = T × Q_t + T × Q_t = T + Q_t = T × Q_t

Bistabilul T sincron are aceleaşi deficienţe ca şi bistabilul JK sincron, legate de durata impusă a semnalului de tact.

Bistabilul T sincron este util în aplicaţiile de numărătoare binare.

Concluzie. Deficienţa principală a structurilor de bistabile studiate este că nu se poate face o distincţie netă între intrările care condiţionează momentul comutării şi cele care determină modul comutării (nu se face distincţie netă între când şi cum).

3.1.6. Bistabile master-slave MS

Bistabilele de tip master-slave introduc un tip de structură care permite rezolvarea comutării bistabilelor. Acest principiul master-slave poate fi aplicat oricărui circuit bistabil.

Structura master-slave este compusă din 2 celule de memorie, una “master” şi cealaltă “slave”.

Master Slave

S S_M Q_M S_S Q_S Q

CLK CLK

R R_M Q_M R_S Q_S Q

CLK

Impulsul de tact are două fronturi, unul pozitiv (de urcare de la 0 la 1, în logica pozitivă) şi unul negativ ¯ (de coborâre de la 1 la 0, în logica pozitivă).

La bistabilele master-slave pe frontul crescător al semnalului de tact se face înscrierea informaţiei în master, slave fiind practic deconectat. Pe frontul descrescător următor se face transferul informaţiei din master în slave şi informaţia va apare la ieşiri după frontul descrescător al impulsului de tact. Se asigură astfel o bună separare între intrările de date şi ieşirile bistabilelor.

S 1 3 Q

2 4 Q

R

CLK

M S

2 3

CLK 1 4 5

Q

t_S t_H

t_S este timpul de set-up = perioada în care datele trebuie să fie pregătite înainte de impulsul de tact.

t_H este timpul de holding.

Pe perioada 1 – 2 a impulsului de ceas, porţile de la intrare nu sunt încă deschise, iar porţile 3,4 se blochează şi astfel izolează slave de master.

Pe zona 2 – 3 porţile de intrare 1,2 se deschid şi informaţia trece în master. Porţile 3,4 sunt închise şi slave îşi păstrează vechea informaţie.

Pe zona 3 – 4 porţile 1,2 se închid şi porţile 3,4 nu se deschid încă: master este izolat de intrare şi de slave.

Pe perioada 4 – 5 porţile 3,4 se deschid, în timp ce porţile 1,2 sunt blocate şi informaţia apare pe ieşire.

Perioada critică este cea de menţinere a datelor la intrare, t_H, pe perioada 4 – 5.

Memorarea se face pe frontul descrescător al impulsului de tact.

Curs 7

3.2. Aplicaţii ale circuitelor basculante bistabile

3.2.1. Numărătoare

Numărătoarele sunt circuite logice secvenţiale care înregistrează numărul de impulsuri aplicate la intrare. Ele se realizează prin asocierea circuitelor basculante bistabile, având rol de celule de memorie binară, cu circuite logice combinaţionale, care determină modul corect în care urmează ca numărătorul să-şi schimbe starea la fiecare nou impuls aplicat la intrare.

Clasificare

Clasificarea numărătoarelor se face după anumite criterii:

1. modul de funcţionare (comutare a bistabililor):

- asincrone – celulele de memorie din care este construit numărătorul nu comută simultan ci aleator;

- sincrone – celulele de memorie din care este construit numărătorul comută simultan sub acţiunea unui impuls de tact aplicat simultan tuturor celulelor.

2. modul de modificare a stărilor (conţinutului):

- directe – îşi cresc conţinutul cu o unitate la fiecare impuls aplicat la intrare;

- inverse – conţinutul scade cu o unitate la fiecare impuls aplicat la intrare;

- reversibile – numără direct sau invers, în funcţie de o comandă aplicată din exterior.

3. modul de codificare a informaţiei:

- binare

- binar-zecimale

- modulo “p” etc.

Numărătoarele se pot realiza cu celule de memorie de tip T care realizează o divizare cu 2. Prin interconectarea a “n” celule de memorie se obţine un numărător cu un număr de stări distincte. Fiecărei stări îi vom asocia câte un cuvânt de cod binar de lungime “n”, reprezentând conţinutul celor “n” celule binare pentru starea dată a numărătorului. Codul în care numără un numărător va fi dat de succesiunea cuvintelor de cod binar asociate stărilor numărătorului.

Numărul stărilor stabile distincte posibile ale unui numărător format din “n” celule binare este 2ⁿ. Dacă din aceste stări se elimină “k” stări rezultă un numărător cu p = 2ⁿ – k stări distincte. Matematic, operaţia realizată de numărător este o operaţie modulo “p”.

Definiţii:

Capacitatea numărătorului = numărul stărilor sale distincte.

Factorul de divizare = raportul dintre numărul de impulsuri de la intrare şi numărul impulsurilor de la ieşire.

Observaţie. Un numărător funcţionează de fapt şi ca un divizor de frecvenţă.

Tipuri de numărătoare

1. Numărător binar asincron direct

Schema logică a numărătorului este realizată prin conectarea în cascadă a bistabililor de tip JK în configuraţie de bistabili de tip T:

Q₀ Q₁ Q₂

J₀ Q₀ J₁ Q₁ J₂ Q₂

CLK₀ CLK₁ CLK₂

K₀ Q₀ K₁ Q₁ K₂ Q₂

1 1 1 R

Q₀, Q₁, Q₂, ieşirile numărătorului, ne dau starea lui la un moment dat.

R este semnalul de Reset, folosit pentru aducerea numărătorului în starea iniţială, la 000.

Intrările bistabililor JK sunt toate legate la “1” logic, deci bistabilii vor comuta la fiecare impuls de tact.

Tact exterior se aplică doar pe intrarea primului bistabil.

Formele de undă pentru numărătorul binar asincron direct sunt:

CLK

Q₀

Q₁

Q₂

Q₂ 0 0 0 0 1 1 1 1

Q₁ 0 0 1 1 0 0 1 1

Q₀ 0 1 0 1 0 1 0 1

Numărătorul este modulo 8, numărând direct în binar, de la 000 la 111. El basculează pe fronturile descrescătoare ale impulsurilor de tact.

Dacă dorim să obţinem valorile numărului în zecimal putem utiliza ieşirile numărătorului, Q₀, Q₁, Q₂, ca şi intrări într-un decodificator binar zecimal.

Dezavantajul numărătorului asincron este că timpul de comutare, în cel mai defavorabil caz, este egal cu suma timpilor de comutare a tuturor bistabililor care îl compun. Avantajul lui constă în simplitatea schemei, realizată doar cu bistabile, prin interconectări directe.

2. Numărător binar asincron invers

Schema logică a numărătorului este:

Q₀ Q₁ Q₂

J₀ Q₀ J₁ Q₁ J₂ Q₂

CLK₀ CLK₁ CLK₂

K₀ Q₀ K₁ Q₁ K₂ Q₂

1 1 1 R

Formele de undă pentru numărătorul binar asincron invers sunt:

CLK

Q₀

Q₁

Q₂

Q₂ 0 1 1 1 1 0 0 0 0

Q₁ 0 1 1 0 0 1 1 0 0

Q₀ 0 1 0 1 0 1 0 1 0

Numărătorul este modulo 8, numărând invers în binar, de la 111 la 000. El basculează pe fronturile descrescătoare ale impulsurilor de tact.

3. Numărător binar asincron reversibil

Numărătorul binar asincron reversibil are celula de memorie de bază ca şi numărătoarele asincrone anterioare, dar între celulele de memorie se intercalează multiplexoare de tip 2:1 prin care se comandă sensul de numărare.

Q₀ Q₁ Q₂

J₀ Q₀ A Mux J₁ Q₁ A Mux J₂ Q₂

CLK₀ 2:1 Y CLK₁ 2:1 Y CLK₂

K₀ Q₀ B K₁ Q₁ B K₂ Q₂

1 1 1 R

S

Pentru S = 0 numărătorul numără direct, iar pentru S = 1 numărătorul numără invers.

4. Numărător binar sincron serie şi paralel

Realizarea numărătoarelor de tip sincron are ca scop creşterea vitezei de comutare a numărătorului în ansamblu.

Funcţionarea acestor numărătoare este sincronă, bistabilii, de tip JK, având intrările de CLK legate împreună. Pe baza tabelului de adevăr se obţine logica combinaţională suplimentară, care asigură funcţionarea corectă a numărătorului.

Nr.	Q0	Q1	Q2	Q3
0	0	0	0	0
1	1	0	0	0
2	0	1	0	0
3	1	1	0	0
4	0	0	1	0
5	1	0	1	0
6	0	1	1	0
7	1	1	1	0
8	0	0	0	1
9	1	0	0	1
10	0	1	0	1
11	1	1	0	1
12	0	0	1	1
13	1	0	1	1
14	0	1	1	1
15	1	1	1	1

Schema logică pentru numărătorul binar sincron serie este:

Q₀ Q₁ Q₂ Q₃

1

S S S S

J Q J Q J Q J Q

CLK CLK CLK CLK

K Q K Q K Q K Q

R R R R

Reset

Intrările J şi K ale primului bistabil sunt legate la 1 “logic” şi vor comuta bistabilul la fiecare tact (conform tabelului de adevăr). Al doilea bistabil comută doar din 2 în 2 impulsuri de tact, adică atunci când Q₀ trece din 1 în 0, deci pot fi legate la ieşirea primului bistabil. Al treilea bistabil basculează din 4 în 4 impulsuri şi va fi comandat de funcţia SI între ieşirile Q₁ × Q₀, iar al patrulea bistabil comută din 8 în 8 impulsuri şi va fi comandat de funcţia SI între ieşirile Q₂ × Q₁ × Q₀. În cazul numărătorului binar sincron de tip serie porţile logice de tip SI utilizate vor fi toate cu 2 intrări, ca în schema logică anterioară.

Pentru mărirea vitezei de răspuns a numărătorului se vor folosi porţi logice de tip SI cu numărul de intrări necesar funcţiei SI implementate, ca în schema de mai jos, corespunzătoare unui numărător binar sincron paralel.

Q₀ Q₁ Q₂ Q₃

1

S S S S

J Q J Q J Q J Q

CLK CLK CLK CLK

K Q K Q K Q K Q

R R R R

CLK

Reset

Timpul de comutare al numărătorului binar sincron paralel este mai mic decât la cel serie, dar există porţi de tip SI cu un număr mai mare de intrări.

5. Numărător binar sincron reversibil

Pentru realizarea reversibilităţii numărătorului binar sincron se folosesc 2 intrări suplimentare, Count-Up (numără direct) şi Count-Down (numără invers). Aceste numărătoare vor avea şi ieşiri pentru transport (Carry) şi împrumut (Borrow), care vor permite legarea în cascadă a numărătoarelor.

Sinteza numărătoarelor modulo p

Pentru a face sinteza unui numărător cu p ¹ 2ⁿ trebuie determinat numărul minim de celule de memorie binară necesare. Relaţia folosită este: 2ⁿ ³ p. Celulele de memorie se interconectează apoi astfel încât să se omită (2ⁿ – p) stări. Din acest motiv există mai multe variante posibile pentru interconectare, deci şi pentru sinteza numărătorului.

Exemplu: Sinteza unui numărător modulo 5.

Pentru 2ⁿ ³ 5 obţinem n = 3, deci vom avea 3 celule de memorie pentru numărător. Numărul stărilor omise va fi 2³ – 5 = 8 – 5 = 3.

Presupunem că avem următoarea succesiune a stărilor de numărare (ciclu de numărare):

000 001 010 011 100

Evident că se putea alege şi altă succesiune a stărilor numărătorului.

Folosim pentru realizarea numărătorului bistabili de tip JK.

Se construieşte un tabel cu stările actuale ale numărătorului, cu stările următoare şi cu condiţionările intrărilor JK ale celor 3 bistabili folosiţi pentru sinteză. Completarea tabelului se face pe baza tabelului de excitaţie al bistabilului JK sincron.

Q_t Q_t+1 J K

0 0 0 x

0 1 1 x

1 0 x 1

1 1 x 0

Q2^t	Q1^t	Q0^t	Q2^t+1	Q1^t+1	Q0^t+1	J2	K2	J1	K1	J0	K0
0	0	0	0	0	1	0	x	0	x	1	x
0	0	1	0	1	0	0	x	1	x	x	1
0	1	0	0	1	1	0	x	x	0	1	x
0	1	1	1	0	0	1	x	x	1	x	1
1	0	0	0	0	0	x	1	0	x	0	x

Diagramele Karnaugh pentru cele 6 intrări ale bistabilelor ne permit determinarea funcţiilor pentru intrări. Stările omise se consideră indiferente.

J₂:

Q2 Q1Q0	00	01	11	10
0			1
1	x	x	x	x

J₂ = Q₁ × Q₀

K₂:

Q2 Q1Q0	00	01	11	10
0	x	x	x	x
1	1	x	x	x

K₂ = 1

J₁:

Q2 Q1Q0	00	01	11	10
0		1	x	x
1		x	x	x

J₁ = Q₀

K₁:

Q2 Q1Q0	00	01	11	10
0	x	x	1
1	x	x	x	x

K₁ = Q₀

J₀:

Q2 Q1Q0	00	01	11	10
0	1	x	x	1
1		x	x	x

J₀ = Q₂

K₀:

Q2 Q1Q0	00	01	11	10
0	x	1	1	x
1	x	x	x	x

K₀ = 1

Schema logică pentru numărătorul modulo 5 va fi următoarea:

Q₂ Q₁ Q₀

J₂ Q₂ J₁ Q₁ J₀ Q₀

CLK CLK CLK

1 K₂ Q₂ K₁ Q₁ 1 K₀ Q₀

R₂ R₁ R₀

CLK

Reset

Pentru rezolvarea completă a sintezei numărătorului modulo 5 trebuie discutată şi problema stărilor omise. Ce se întâmplă cu numărătorul dacă nu are secvenţă de iniţializare sau dacă ajunge cumva în una dintre stările care nu face parte din ciclul de numărare? Care va fi evoluţia numărătorului?

Trebuie verificate tranziţiile numărătorului în cazul în care este într-o stare din afara ciclului de numărare. Putem avea 2 situaţii: fie numărătorul revine singur în ciclul de numărare, fie trebuie reproiectat astfel încât să revină în ciclul de numărare.

Stările omise în exemplul dat sunt:

101 ® 010

110 ® 010 şi din starea aceasta se revine în ciclu

111 ® 010

Observaţie. Un numărător modulo p se poate obţine folosind un numărător binar sincron. Se lasă numărătorul binar să evolueze până la starea p-1. La atingerea stării “p” se aplică numărătorului, printr-o logică combinaţională, un impuls de ştergere (pe intrarea de Reset).

Numărătoare Moebius

Numărătoarele Moebius sunt numărătoare în inel cu coadă întoarsă (twisted tail ring counter).

Deşi există numărătoare de tip MSI pentru numărarea binară sau a altor tipuri de secvenţe, există unele cazuri în care se preferă proiectarea unor numărătoare speciale cu bistabili şi porţi logice.

Exemplu: un numărător cu 8 stări la care la fiecare tranziţie se modifică numai un singur bit, se poate construi utilizând următoarea secvenţă:

0000 0

1000 8

1100 12

1110 14

1111 15

0111 7

0011 3

0001 1

Proiectarea se face şi cu bistabili de tip D şi cu bistabili de tip JK.

Tabelul folosit pentru sinteza numărătorului este:

Q3^t	Q2^t	Q1^t	Q0^t	Q3^t+1	Q2^t+1	Q1^t+1	Q0^t+1	D3	D2	D1	D0	J3	K3	J2	K2	J1	K1	J0	K0
0	0	0	0	1	0	0	0	1	0	0	0	1	x	0	x	0	x	0	x
1	0	0	0	1	1	0	0	1	1	0	0	x	0	1	x	0	x	0	x
1	1	0	0	1	1	1	0	1	1	1	0	x	0	x	0	1	x	0	x
1	1	1	0	1	1	1	1	1	1	1	1	x	0	x	0	x	0	1	x
1	1	1	1	0	1	1	1	0	1	1	1	x	1	x	0	x	0	x	0
0	1	1	1	0	0	1	1	0	0	1	1	0	x	x	1	x	0	x	0
0	0	1	1	0	0	0	1	0	0	0	1	0	x	0	x	x	1	x	0
0	0	0	1	0	0	0	0	0	0	0	0	0	x	0	x	0	x	x	1

Diagramele Karnaugh ne permit să determinăm valorile pentru intrările bistabilelor D₃ – D₀ şi J₃ – K₀.

D₃:

Q3Q2 Q1Q0	00	01	11	10
00	1			x
01	x	x		x
11	1	x		1
10	1	x	x	x

D₃ = Q₀

D₂:

Q3Q2 Q1Q0	00	01	11	10
00				x
01	x	x		x
11	1	x	1	1
10	1	x	x	x

D₂ = Q₃

D₁:

Q3Q2 Q1Q0	00	01	11	10
00				x
01	x	x	1	x
11	1	x	1	1
10		x	x	x

D₁ = Q₂

D₀:

Q3Q2 Q1Q0	00	01	11	10
00			1	x
01	x	x	1	x
11		x	1	1
10		x	x	x

D₀ = Q₁

J₃:

Q3Q2 Q1Q0	00	01	11	10
00	1			x
01	x	x		x
11	x	x	x	x
10	x	x	x	x

J₃ = Q₀

K₃:

Q3Q2 Q1Q0	00	01	11	10
00	x	x	x	x
01	x	x	x	x
11		x	1
10		x	x	x

K₃ = Q₀

J₂:

Q3Q2 Q1Q0	00	01	11	10
00				x
01	x	x	x	x
11	x	x	x	x
10	1	x	x	x

J₂ = Q₃

K₂:

Q3Q2 Q1Q0	00	01	11	10
00	x	x	x	x
01	x	x	1	x
11		x
10	x	x	x	x

K₂ =Q₃

J₁:

Q3Q2 Q1Q0	00	01	11	10
00			x	x
01	x	x	x	x
11	1	x	x	x
10		x	x	x

J₁ = Q₂

K₁:

Q3Q2 Q1Q0	00	01	11	10
00	x	x	1	x
01	x	x		x
11	x	x
10	x	x	x	x

K₁ = Q₂

J₀:

Q3Q2 Q1Q0	00	01	11	10
00		x	x	x
01	x	x	x	x
11		x	x	1
10		x	x	x

J₀ = Q₁

K₀:

Q3Q2 Q1Q0	00	01	11	10
00	x	1		x
01	x	x		x
11	x	x		x
10	x	x	x	x

K₀ = Q₁

Cele 2 scheme logice pentru numărător sunt:

D₃ Q₃ D₂ Q₂ D₁ Q₁ D₀ Q₀

CLK Q₃ CLK Q₂ CLK Q₁ CLK Q₀

CLK

J₃ Q₃ J₂ Q₂ J₁ Q₁ J₀ Q₀

CLK CLK CLK CLK

K₃ Q₃ K₂ Q₂ K₁ Q₁ K₀ Q₀

CLK

Observaţie. Starea fiecărui bistabil este determinată de starea anterioară a bistabilului plasat în stânga sa, iar starea primului bistabil este determinată de ieşirea complementară a ultimului bistabil.

Se pot construi numărătoare Moebius de orice dimensiune (ordin).

Aplicaţii ale numărătoarelor Moebius

a. Se pot folosi ca şi numărătoare de stare. Dacă numărătorul este implementat cu bistabile JK, fiecare comutare a stării este controlată de câte o intrare diferită. Din acest motiv, modificarea oricărei stări va putea fi controlată independent, adăugând o poartă SI sau SI-NU pe intrarea respectivă (de exemplu tranziţia 0 ® 8 este controlată de J₃, tranziţia 8 ® 12 de J₂ ş.a.m.d.).

b. Generatoare de ceas cu mai multe faze. Cele 8 ieşiri ale numărătorului generează de fapt 8 semnale de ceas defazate în mod egal, cu factor de umplere de 50%. În general un numărător Moebius de n biţi generează 2n faze de ceas.

c. Decodificarea oricărei stări se poate face printr-o poartă cu 2 intrări. Pt. a face decodificarea stării se vor urmări cei 2 biţi adiacenţi distincţi, 1 şi 0.

d. Decodificarea stărilor succesive se realizează prin porţi care au ca intrări ultimul 1 al primei stări şi primul 0 al ultimei stări.

Curs 8

3.2.2. Registre

Registrele sunt circuite logice secvenţiale care permit stocarea şi/sau deplasarea informaţiei codificate binar. Ele se realizează din celule de memorie binară (CBB) şi din circuite logice combinaţionale (CLC), care permit înscrierea, citirea şi transferul informaţiei. Capacitatea unui registru este dată de numărul celulelor de memorie.

Orice informaţie binară, care nu depăşeşte capacitatea registrului, poate fi înscrisă prin acţionarea corespunzătoare a intrărilor (care depinde şi ea de natura bistabilelor).

Registrele pot să fie de mai multe tipuri: de memorie; de deplasare; combinate; universale.

Registrele de memorie memorează informaţia binară în celule de memorie binară. În fiecare celulă de memorie se memorează un bit de informaţie. Încărcarea se poate face paralel, prin intrările asincrone, de Set şi Reset.

Registrele de deplasare sunt cele care realizează transferul informaţiei. Transferul se poate face: stânga-dreapta; dreapta-stânga; în ambele sensuri.

La fiecare impuls de tact conţinutul registrului se deplasează cu câte o celulă (în sensul stabilit). Semnalul de ieşire este identic cu cel de intrare, dar întârziat cu un număr de impulsuri de tact egal cu numărul de celule de memorie din care este format registrul.

Exceptând primul bistabil, ecuaţia de stare a unui registru de deplasare stânga-dreapta este dată de relaţia: Q_i(t+1) = Q_i-1(t) × c (unde c = impulsul de tact).

Exemplu: Registru de deplasare stânga-dreapta cu bistabile JK MS.

Q₀ Q₁ Q₂ Q₃

S_IN

J₀ Q₀ J₁ Q₁ J₂ Q₂ J₃ Q₃

CLK CLK CLK CLK

K₀ Q₀ K₁ Q₁ K₂ Q₂ K₃ Q₃

R R R R

Reset

CLK

La fiecare impuls de tact conţinutul bistabilului Q_i se transferă în bistabilul Q_i+1. În bistabilul Q₀ se introduce informaţia din exterior, iar conţinutul ultimului bistabil se pierde. Încărcarea registrului se realizează deci în mod serie. Iniţializarea registrului se face prin semnalul de Reset, care forţează toate ieşirile registrului în 0 logic.

Registrele de deplasare dreapta-stânga şi reversibile se realizează folosind circuite logice combinaţionale suplimentare.

Registrele combinate sunt cele care au şi funcţia de memorare şi cea de deplasare.

Registrele universale cumulează toate funcţiile: deplasare stânga-dreapta, deplasare dreapta-stânga, încărcare serie sau paralelă a informaţiei, citire serie sau paralelă a informaţiei.

RI A B C D LI

S₀

S₁

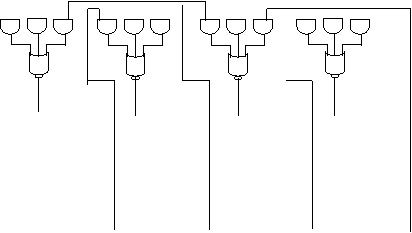
D Q D Q D Q D Q

CLK CLK CLK CLK CLK

CLR CLR CLR CLR

CLR

Q₀ Q₁ Q₂ Q₃

Intrările de selecţie S₁S₀ condiţionează modul de funcţionare a registrului. Avem:

S₁S₀ = 00 păstrează conţinutul nemodificat;

S₁S₀ = 01 deplasare stânga-dreapta;

S₁S₀ = 10 deplasare dreapta-stânga;

S₁S₀ = 11 încărcare paralelă.

Ştergerea registrului se face asincron, prin semnalul CLR.

Aplicaţii ale registrelor

Registrele sunt utilizate în mai multe tipuri de aplicaţii, după funcţiile pe care pot să le îndeplinească.

1. Registre de deplasare cu reacţie

Au ieşirile conectate la intrări şi pot fi:

- registre de deplasare în inel – conţinutul ultimei celule de memorie se înscrie în prima celulă de memorie;

Q₀ Q₁ Q₂ Q₃

1 0 0 0

S_IN 0 1 0 0

0 0 1 0

Q₀ Q₁ Q₂ Q₃ 0 0 0 1

1 0 0 0

- registre (numărătoare) Johnson – în prima celulă se introduce conţinutul negat al ultimei celule.

Q₀ Q₁ Q₂ Q₃

0 0 0 0

S_IN 1 0 0 0

1 1 0 0

Q₀ Q₁ Q₂ Q₃ 1 1 1 0

1 1 1 1

0 1 1 1

0 0 1 1

0 0 0 1

0 0 0 0

2. Memorie de tip FIFO (First In, First Out), primul înscris – primul citit (memorie coadă)

Se realizează cu registre de deplasare stânga-dreapta. Numărul registrelor depinde de lungimea cuvintelor ce urmează a fi memorate. Capacitatea memoriei depinde de lungimea registrelor. De exemplu, dacă registrele sunt de 4 biţi, capacitatea memoriei este de 4 cuvinte. La fiecare impuls de tact se introduc datele pe intrarea serială.

y₁

S_IN Ts

x₁

y₂

S_IN Ts

x₂

y₃

S_IN Ts

x₃

y₄

S_IN Ts

x₄

CLK

3. Memorie de tip LIFO (Least In, First Out), ultimul introdus – primul citit (memorie stivă)

Realizarea se face cu registre combinate. Numărul registrelor este dat de lungimea cuvântului de memorie, iar lungimea registrelor determină capacitatea de memorie.

x_i

A₀

A₁

A₁ A₀

S_IN Q₀ y_i

Q₁

Q₂

Q₃

R CLK

A₁ A₀

0 1 deplasare stânga-dreapta ® înscriere

1 0 citire

Memoria stivă poate fi organizată şi soft, în memoria de tip RAM, dar deşi capacitatea acesteia poate fi mare, timpul de acces va fi şi el mare.

4. Conversia serie-paralel şi paralel serie a informaţiei

Pentru conversia serie-paralel se face încărcarea registrului pe intrarea serială şi cu comandă de tact serie Ts şi se citeşte informaţia pe ieşiri, paralel.

Pentru conversia paralel-serie se face încărcarea paralelă a informaţiei, cu comandă de tact paralel Tp şi apoi se deplasează informaţia stânga-dreapta, cu comandă de tact serie Ts şi se citeşte serie la ultima ieşire.

5. Generatoare de secvenţe

Generatoarele de secvenţe generează o succesiune de secvenţe binare (1 şi 0) de lungime dată (prestabilite). Lungimea secvenţei reprezintă numărul de biţi după care se repetă întreaga secvenţă. Secvenţele binare pot fi:

- aleatoare, de lungime infinită;

- deterministe, de lungime finită.

Secvenţele binare deterministe de lungime maximă se numesc secvenţe pseudoaleatoare.

Realizarea generatoarelor de secvenţe se face cu registre în reacţie cu circuite logice combinaţionale adecvate.

Q₀ Q₁ Q₂

y = Q₀ + Q₂

S₀ Q₀ S₁ Q₁ S₂ Q₂

CLK CLK CLK

R₀ Q₀ R₁ Q₁ R₂ Q₂

CLK

Secvenţa pseudoaleatoare generată la ieşirile Q₀Q₁Q₂ este:

100 ® 110 ® 111 ® 011 ® 101 ® 010 ® 001

3.2.3. Memorii RAM

Memoriile de tip RAM (random access memory) sunt memorii de tip citeşte-scrie, cu acces aleator. Ele nu-şi păstrează informaţia după întreruperea tensiunii de alimentare.

Memoria este formată din nivelul de decodificare, matricea de memorie realizată cu celule de memorie binară de tip “latch” şi nivelul de multiplexare.

Dimensiunea memoriei este specificată prin numărul de cuvinte şi numărul de biţi pe cuvânt. Capacitatea memoriei este dată de numărul de biţi memoraţi în matricea de memorie.

Schema funcţională de principiu a unei memorii RAM este următoarea:

Adresă CE sau CS (chip select)

n Decodificator

2ⁿ

n Matrice de

memorie

2ⁿ

WE (write enable)

Multiplexor

Date

Decodificatorul acţionează pentru selectarea fiecărei celule de memorie, iar multiplexorul permite selectarea oricărei celule de memorie la intrare – ieşire.

Validarea memoriei se face prin intrarea CS. Citirea memoriei se face dacă WE = 1, iar scrierea memoriei se face dacă WE = 0.

Datele de intrare şi ieşire pot să folosească linii diferite sau aceeaşi linie bidirecţională. Memoriile pot avea un număr diferit de căi de date (de obicei cuvinte de 1 bit sau de un număr de biţi multiplu de 2).

Memoriile de tip RAM pot să fie din punct de vedere constructiv de tip static sau dinamic. Cele dinamice sunt realizate cu condensatoare şi au nevoie de reîmprospătarea la diferite intervale de timp a informaţiei memorate, pentru a se evita pierderea ei.

Extinderea capacităţii memoriilor se face atât prin extinderea dimensiunii cuvântului de memorie (numărul de biţi din cuvânt), cât şi prin extinderea numărului de cuvinte ale memoriei (adresa de memorie).

Curs 9

3.3. Sinteza circuitelor logice secvenţiale sincrone

Circuitele secvenţiale sincrone trec dintr-o stare în alta la momente distincte de timp, determinate de impulsurile de tact. Între două impulsuri de tact starea circuitului nu se modifică.

Variabile de intrare

Generare stare nouă

Calculul excitaţiilor secundare

CLC

Excitaţii secundare

Tact

Registru de stări

Stări interne

CL

Variabile secundare

Calculul variabilelor de ieşire

CLC

CL = circuit logic general – păstrează starea internă ® registru de stări (bistabili RS, D, JK, registre, memorii); poate fi circuit logic secvenţial cu buclă de reacţie.

CLC = determină funcţiile de excitaţie secundare care în prezenţa tactului determină trecerea circuitului în altă stare ® se poate numi generatorul stării noi; se pot realiza cu porţi logice sau cu circuite specializate (multiplexoare, decodificatoare).

Variabilele de intrare sunt în general sincrone cu impulsul de tact, dar pot fi şi de tip asincron.

3.3.1. Etapele de sinteză

1. Expunerea condiţiilor de funcţionare (descrierea comportării circuitului).

Stabilirea modalităţii de definire a circuitului care trebuie sintetizat prin:

- tabel de tranziţii;

- graf de tranziţii;

- organigramă;

- forme de undă.

Trebuie evidenţiate:

- stările prin care trece circuitul;

- valorile variabilelor de intrare pentru care se schimbă stările;

- valorile rezultate ale variabilelor de ieşire.

Evoluţia circuitului începe într-o stare iniţială şi de obicei se revine la această stare, după ultima stare a ciclului.

2. Se codifică stările circuitului.

3. Se încearcă reducerea (simplificarea) numărului de stări a circuitului, dacă este posibil, încât să se păstreze funcţionarea lui corectă.

4. Se decide asupra modului de implementare (registrul de stări interne).

5. Se determină funcţiile de excitaţie şi cele de ieşire, dacă este posibil.

6. Se studiază problemele legate de eventualele ieşiri false (hazard) sau tranziţii false.

7. Se desenează circuitul.

Etapa cea mai dificilă este cea de codificare a stărilor. În general funcţionările defectuoase se datorează unor tranziţii greşite între stări sau unor semnale greşite care apar la circuitul de generare a variabilelor de ieşire.

Tranziţiile greşite între stări apar datorită prezenţei variabilelor de intrare asincrone (se elimină cel mai uşor dacă se sincronizează variabilele de intrare cu semnalul de tact).

Codificarea stărilor se stabileşte astfel încât, în orice stare, pentru toate combinaţiile posibile de intrări asincrone, să nu fie mai mult decât o singură variabilă de stare dependentă de o variabilă de intrare asincronă. În aceste condiţii, două stări rezultate din calea de ieşire a unei intrări asincrone vor avea codificare adiacentă.

Ieşirile false pot să apară din cauză că la trecerea dintr-o stare în alta, variabilele de stare practic nu se modifică simultan. Pentru evitarea tranziţiilor false ale ieşirilor se pot folosi metodele:

- se realizează o codificare adiacentă a stărilor;

- se forţează trecerea circuitului prin stări suplimentare;

- se sincronizează variabilele de ieşire.

Observaţie: Hazardul static al CLC se elimină prin proiectare (se introduc termeni redundanţi, indiferenţi).

3.3.2. Utilizarea organigramei în sinteza circuitelor logice secvenţiale sincrone

Elementele componente ale organigramei de funcţionare a oricărui circuit secvenţial sincron sunt:

- elementul de intrare (control sau decizie):

Variabile de intrare

- sincrone

var. 1

0

- asincrone

var. 1

0

- elementul de stare:

Q₂Q₁Q₀

000

- elementul de ieşire:

transfer

Configuraţii elementare care unesc cele 3 elemente de bază:

A 001 tranziţie simplă:

- contor de timp

- soluţionarea problemei de codificare a stărilor

B 011

A stare cu ieşire

Adună

B

A stare cu decizie

1 I₁ 0

B C

A stare cu ieşire şi decizie

Scade

1 I₁ 0

B C

A stare cu ieşire condiţionată

I₁ 1

0 Ieşire

B

A stări cu decizii multiple şi ieşire

0 I₁ 1

1

I₂ C

0 1 0

I₃

B Ieşire

Observaţii

1. Orice tranziţie între 2 stări ale circuitului se face într-un singur impuls de tact.

2. La un moment dat circuitul se poate găsi într-o singură stare.

3. Un circuit care se găseşte la un moment dat într-o stare dată, cu un set de intrări dat, poate avea o singură stare următoare.

3.3.3. Sinteza circuitelor secvenţiale sincrone cu diferite elemente de memorie

În sinteza circuitelor secvenţiale sincrone se vor folosi ca elemente de memorie bistabili de tip D şi JK. Implementarea registrului de stări se va realiza cu aceste tipuri de bistabile.

Exemplu: Să se recunoască secvenţa 101 în şirul de cifre binare 10101.

Graful de tranziţii are în noduri stările circuitului. Pe arce avem tranziţia dintr-o stare în alta pentru o anumită intrare, cu o anumită ieşire.

0/0 1/0

1/0 0/0

Init A B C

1/1

0/0

Avem 2 variabile de stare pentru a putea codifica 2 stări (A=00, B=01, C=11). Cu x am notat intrarea, cu z ieşirea. Tabelul de tranziţii este:

S_t S_t+1,z

Q₁Q₀ x=0 x=1

00 A A,0 B,0

01 B C,0 B,0

11 C A,0 B,1

a. Implementăm registrul de stări cu bistabile de tip D.

Funcţiile de excitaţie se deduc explicitând diagrama stărilor pentru momentul t şi momentul t+1. Stările se vor înlocui cu codurile lor (A=00, B=01, C=11).

S_t S_t+1 (Q₁Q₀)^t+1 z

Q₁Q₀ D₁D₀ D₁D₀

x=0 x=1 x=0 x=1

00 (A) 00 (A) 01 (B) 0 0

01 (B) 11 (C) 01 (B) 0 0

11 (C) 00 (A) 01 (B) 0 1

D_i = Q_i^t ecuaţia stării următoare

D₁:

Q1Q0 x	0	1
00	0	0
01	1	0
11	0	0
10	x	x

D₁ = Q₁ × Q₀ × x

D₀:

Q1Q0 x	0	1
00	0	1
01	1	1
11	0	1
10	x	x

D₀ = x + Q₁ × Q₀

z:

Q1Q0 x	0	1
00	0	0
01	0	0
11	0	1
10	x	x

z = Q₁ × x

La trecerea din starea C în starea A se poate trece prin starea B, ceea ce nu corespunde funcţionării. În mod normal se introduce o stare suplimentară pentru a rezolva situaţia.

Schema pentru circuitul secvenţial sincron este:

D₁ Q₁ D₀ Q₀ Q₁

CLK CLK Q₀ D₁

Q₁ Q₀ x

R R Q₀

Init Q₁ D₀

x

CLK Q₁ z

x

b. Implementăm registrul de stări cu bistabile de tip JK.

Diagrama stărilor se completează ţinând cont de tabelul de excitaţie al bistabilului JK.

Q_t Q_t+1 J K

0 0 0 x

0 1 1 x

1 0 x 1

1 1 x 0

S_t S_t+1(Q₁Q₀)^t+1 z

Q₁Q₀ J₁K₁ J₀K₀ J₁K₁ J₀K₀

x=0 x=1 x=0 x=1 x=0 x=1

00 (A) 00 01 0x 0x 0x 1x 0 0

01 (B) 11 01 1x x0 0x x0 0 0

11 (C) 00 01 x1 x1 x1 x0 0 1

J₁:

Q1Q0 x	0	1
00	0	0
01	1	0
11	x	x
10	x	x

J₁ = Q₀ × x

K₁:

Q1Q0 x	0	1
00	x	x
01	x	x
11	1	1
10	x	x

K₁ = 1

J₀:

Q1Q0 x	0	1
00	0	1
01	x	x
11	x	x
10	x	x

J₀ = x

K₀:

Q1Q0 x	0	1
00	x	x
01	0	0
11	1	0
10	x	x

K₀ = Q₁ × x

z:

Q1Q0 x	0	1
00	0	0
01	0	0
11	0	1
10	x	x

z = Q₁ × x

3.3.4. Implementarea generatorului noii stări cu multiplexoare

Pentru a realiza o implementare cu multiplexoare se scriu funcţiile de excitaţie pentru bistabile în forma canonică (fără a se minimiza).

Se iau în considerare locaţiile care sunt 1 sau care au o variabilă înglobată.

x

CLC

MUX

Registru de stare

CLC

y

3.3.5. Implementarea generatorului noii stări cu decodificatoare

În cazul implementării generatorului noii stări cu decodificatoare, la intrarea decodificatorului sunt aplicate variabilele de stare, iar la ieşire sunt individualizate stările interne.

3.3.6. Implementarea generatorului noii stări cu memorii şi multiplexoare

Acest tip de implementare a generatorului noii stări se utilizează în cazul circuitelor complexe. Se asigură o simplificare a logicii de generare a noii stări şi o creştere a siguranţei în funcţionare.

Implementarea generatorului noii stări cu decodificatoare:

x

CLC

Registru de stări

DEC

CLC

y

Implementarea generatorului noii stări cu multiplexoare şi memorii:

x

MUX

Memorie

Registru de stări

CLC

y

Curs 10

Exemplu: Sinteza unui automat (circuit secvenţial sincron) de răspuns la telefon. Se poate programa numărul de apeluri sonore ale soneriei telefonului după care începe să funcţioneze automatul. Programul automatului se încheie în condiţiile: 1) după preluarea (înregistrarea) mesajului; 2) dacă apelantul închide; 3) dacă destinatarul răspunde la telefon.

1. Determinarea funcţionării – obţinerea organigramei.

Se stabileşte schema bloc a automatului, cu componentele periferice adiţionale necesare. Se stabilesc variabilele de intrare şi ieşire şi caracterul lor sincron sau asincron.

Avem nevoie de:

- telefon propriu-zis (TEL);

- numărător pentru apelurile sonore ale soneriei telefonului (NRT);

- casetofon pentru redarea mesajului de întâmpinare (PLAY);

- casetofon pentru înregistrarea mesajului apelantului (REC).

Variabilele folosite sunt:

Sonerie: fiecare apel al soneriei telefonului provoacă decrementarea numărătorului NRT până ce ajunge la 0. Nu este variabilă a automatului.

Start: variabilă de intrare asincronă, de la numărător, care determină începerea funcţionării automatului, dacă numărătorul a ajuns pe 0.

StartPlay (SP), StartRecord (SR): variabile de ieşire spre casetofon.

EndOfPlay (EP), EndOfRecord (ER): variabile de intrare asincrone, de la casetofon.

ApelantStop (AS): variabilă de intrare asincronă de la telefon (apelantul poate închide oricând telefonul).

DestinatarPick-Up (DPU): variabilă de intrare asincronă de la telefon; apare când destinatarul răspunde la telefon.

Init: variabilă de ieşire spre numărător; încarcă paralel numărătorul cu valoarea stabilită pentru numărul de apeluri ale soneriei telefonului până la intrarea în funcţiune a automatului.

Obs: variabilele de intrare AS şi DPU generează semnalul de Reset pentru bistabilii interni ai automatului şi opresc înregistrarea pe casetofon.

Schema bloc este:

CLK Sonerie

PL NRT TEL

Zero AS DPU

Start

Init Automat ER

SP

EP SR

PLAY REC

Organigrama automatului este:

000

A

Init

1 0

Start

B 001

SP

011 C

1 0

EP

D 010

SR

100 E

1 0

ER

2. Codificarea stărilor

Pentru că variabilele de intrare sunt asincrone este nevoie de o codificare adiacentă a stărilor automatului (A,B), (C,D), (E,A) . Pentru 5 stări sunt necesare 3 variabile de stare pentru codificare. Se alege codificarea: A = 000; B = 001; C = 011; D = 010; E = 100.

Se construieşte diagrama Karnaugh pentru stări, pe baza codificării făcute:

Q2 Q1Q0	00	01	11	10
0	A	B	C	D
1	E

Trebuie obţinute diagramele pentru stările următoare. Le vom suprapune şi vom desena o singură diagramă, înglobând şi variabilele de intrare. Completarea se face urmărind tranziţiile din organigramă şi completând pentru fiecare stare codul stării următoare. Locaţiile necompletate vor fi indiferente deoarece conţinutul lor nu poate fi atins prin funcţionare.

Q2 Q1Q0	00	01	11	10
0	00Start	011	01EP	100
1	ER00

3. Reducerea numărului de stări nu mai este posibilă.

4. şi 5. Registrul de stări se implementează cu bistabile de tip D, iar generatorul noii stări (funcţiile de excitaţie) şi ieşirile cu porţi logice.

a. Pentru implementarea registrului de stări cu bistabile de tip D se ţine cont de ecuaţia stării următoare a acestui tip de bistabil: D_i = Q_i^t.

Diagramele Karnaugh pentru intrările bistabilelor vor fi:

D₂:

Q2 Q1Q0	00	01	11	10
0	0	0	0	1
1	ER	x	x	x

D₂ = ER × Q₂ + Q₁ × Q₀

D₁:

Q2 Q1Q0	00	01	11	10
0	0	1	1	0
1	0	x	x	x

D₁ = Q₀

D₀:

Q2 Q1Q0	00	01	11	10
0	Start	1	EP	0
1	0	x	x	x

D₀ = Start × Q₂ × Q₁ + EP × Q₀ + Q₁ × Q₀

Diagramele ieşirilor se completează ţinând cont de organigramă şi de diagrama stărilor.

Init:

Q2 Q1Q0	00	01	11	10
0	1
1		x	x	x

Init = Q₂ × Q₁ × Q₀

SP:

Q2 Q1Q0	00	01	11	10
0		1
1		x	x	x

SP = Q₁ × Q₀

SR:

Q2 Q1Q0	00	01	11	10
0				1
1		x	x	x

SR = Q₁ × Q₀

7. Desenarea schemei circuitului

Ieşirile se realizează cu porţi logice de tip SI:

Q₂

Q₁ Init

Q₀

Q₂ SP

Q₁

Q₀ SR

Generarea semnalului de Reset se realizează cu o poartă logică SAU-NU:

Reset = AS + DPU

AS

Reset

DPU

Registrul de stări este cu bistabile de tip D:

D₂ Q₂ D₁ Q₁ D₀ Q₀

Clk Clk Clk

Q₂ Q₁ Q₀

R R R

Clk

Reset

Funcţiile de excitaţie se implementează cu porţi logice:

Q₂ D₀

Q₁

Q₀

Q₂

Q₁ D₂

Q₀ D₁

Start

ER

EP

b. Implementarea generatorului noii stări cu multiplexoare se poate realiza numai cu multiplexoare dacă numărul intrărilor de selecţie a multiplexorului este egal cu numărul variabilelor de stare. Dacă numărul intrărilor de selecţie este mai mic decât cel al variabilelor de stare, la intrările selectate se vor conecta circuite realizate cu porţi logice.

Se scriu termenii canonici care conţin 1 sau variabile înglobate in diagrama Karnaugh.

D₂ = Q₂ × Q₁ × Q₀ + ER × Q₂ × Q₁ × Q₀

D₁ = Q₂ × Q₁ × Q₀ + Q₂ × Q₁ × Q₀

D₀ = Start × Q₂ × Q₁ × Q₀ + EP × Q₂ × Q₁ × Q₀ + Q₂ × Q₁ × Q₀

Implementarea cu MUX 8:1 este:

0

0 MUX

1 8:1

0 D₂

ER D₂

0 74151

0

0 s₂ s₁ s₀

Q₂ Q₁ Q₀

0

1 MUX

0 8:1

1 D₁

0 D₁

0 74151

0

0 s₂ s₁ s₀

Q₂ Q₁ Q₀

Start

1 MUX

0 8:1

EP D₀

0 D₀

0 74151

0

0 s₂ s₁ s₀

Q₂ Q₁ Q₀

Dacă implementarea s-ar realiza cu MUX 4:1 pe intrările multiplexorului am avea ieşiri din porţi logice de tip SI.

c. Implementarea generatorului noii stări cu decodificatoare se face aplicând la intrarea decodificatorului variabilele de stare. La ieşirile decodificatorului se obţin stările interne individualizate.

Putem scrie:

D₂ = D + ER × E

D₁ = B + C

D₀ = Start × A + B + EP × C

Pentru obţinerea funcţiilor de excitaţie se vor utiliza porţi logice de tip SI, SAU şi NU.

Decodificatorul va fi de tip zecimal:

DCD 0 A

0 1 B D₁

Q₂ 2 D

Q₁ 3 C

Q₀ 4 E

9

d. Implementarea generatorului noii stări cu memorii şi multiplexoare permite simplificarea logicii generării noii stări.

ROM A₀ MUX 0 Start

16 x 4 A₁ 8:1 1 0

A₂ 2 0

y₃ y₂ y₁ y₀ A₃ Y 3 EP

4 ER 5 0

D₂ Q₂ D₁ Q₁ D₀ Q₀ 6 0

Clk Clk Clk s₂ s₁ s₀ 7 0

Q₂Q₁Q₀ A₃A₂A₁A₀ y₃y₂y₁y₀ Q₂Q₁Q₀ A₃A₂A₁A₀ y₃y₂y₁y₀

(s₂s₁s₀) (s₂s₁s₀)

000 0000 0000 000 1000 0001

001 0001 0011 001 1001 0000

010 0010 0100 010 1010 0000

011 0011 0010 011 1011 0011

100 0100 0000 100 1100 0100

101 0101 0000 101 1101 0000

110 0110 0000 110 1110 0000

111 0111 0000 111 1111 0000

e. Implementarea circuitelor secvenţiale sincrone se poate realiza cu numărătoare MSI. Numărătorul va fi utilizat pentru funcţia de memorare şi parţial pentru efectuarea tranziţiilor.

Vom utiliza pentru implementare un numărător sincron (de exemplu numărătorul zecimal 74162). Bistabilii interni ai acestuia pot memora starea circuitului.

Codificarea stărilor se face ţinând cont de ordinea de numărare a numărătorului: A = 000; B = 001; C = 010; D = 011; E = 100.

Q2 Q1Q0	00	01	11	10
0	A	B	D	C
1	E

Vom determina funcţiile de numărare f_N şi încărcare (ramificare) f_R şi vom realiza implementarea lor cu multiplexoare 8:1 (de tipul 74151). Intrările de selecţie vor fi ieşirile numărătorului, Q₂Q₁Q₀. Diagramele pentru cele 2 funcţii vor fi:

f_N:

Q2 Q1Q0	00	01	11	10
0	Start	1	1	EP
1

f_R:

Q2 Q1Q0	00	01	11	10
0
1	ER

Stările următoare ale numărătorului trebuie specificate pentru stările din care au loc ramificări (E). D₂ = Q₂; D₁ = Q₁; D₀ = Q₀. În acest caz se utilizează încărcarea paralelă a numărătorului cu valoarea prestabilită pe intrările paralele.

Schema circuitului trebuie completată şi cu logica pentru determinarea ieşirilor. Ieşirile Init, SP şi SR corespund stărilor A, B, D. Funcţiile de ieşire sunt:

Init = Q₂ × Q₁ × Q₀

SP = Q₁ × Q₀

SR = Q₁ × Q₀

Implementarea funcţiilor de ieşire se poate realiza cu porţi logice de tip SI sau cu un decodificator zecimal.

Circuitul secvenţial sincron va avea următoarea implementare:

0 0 En Start 0 En

0 1 MUX 1 1 MUX

0 2 8:1 EP 2 8:1

0 3 f_R 1 3 f_N

ER 4 Y 0 4 Y

0 5 Y 0 5 Y 0 Init

0 6 0 6 DCD 1 SP

0 7 4151 0 7 4151 2

s₂ s₁ s₀ s₂ s₁ s₀ 0 D₃ 3 SR

D₂ 4

D₁ 5

D₀ 6

7

Q₃Q₂Q₁Q₀ 7442 8

Reset MR 74162 Clk 9

LD D₃D₂D₁D₀ EN

0

Curs 11

3.4. Sisteme secvenţiale sincrone

Evoluţia circuitelor secvenţiale sincrone a fost determinată de metodele de sinteză adecvate. Pentru circuitele secvenţiale sincrone cu număr mic de variabile de intrare şi de stare se poate utiliza sinteza pornind de la grafuri sau diagrame de tranziţii (metoda studiată). Pentru circuitele cu număr mare de variabile de intrare şi de stare se face o organigramă funcţională care pune în evidenţă direct stările interne şi tranziţiile, în funcţie de modificarea unei singure variabile de intrare. Aceste circuite se numesc sisteme secvenţiale sincrone (SSS).

Structura unui sistem secvenţial sincron:

START

Încărcare R S₁

numărător C = 0 căutarea biţilor = 1

într-un registru de 8 biţi

DA R_i = 1 NU S₂

Prelucrare în funcţie Deplasare stânga R S₃

de rangul bitului C = C – 1

(succesiune de operaţii)

NU S₄

C = 8

DA

STOP

Analiza figurii permite determinarea a 2 blocuri funcţionale:

1. Unitatea de execuţie UE – realizată cu regiştri, numărătoare, bistabili, CLC.

2. Generatorul de secvenţe sau unitatea de comandă UC – secvenţiator care operează asupra unităţii de execuţie. UC trebuie să asigure:

- trecerea din starea S_i în starea S_i+1;

- întreruperi de secvenţe prin salt;

- bucle de aşteptare.

Schema sistemului secvenţial complex

UC UE

Calculul secvenţei Stări

următoare

Generator

de tact Unitate de

CLK execuţie UE

Generator de

secvenţe

secvenţe

Bloc de determinare acţiune

CLK a acţiunii asupra UE UE

Unităţile de comandă UC pot fi: cablate sau microprogramate. Generatorul de secvenţe poate deci fi realizat cablat sau microprogramat.

1) UC cablate – există 2 posibilităţi de realizare:

a. Generatorul de secvenţe este realizat cu un numărător programabil. Acesta numără, se opreşte sau se încarcă cu o nouă valoare. Ieşirile sale sunt decodificate de un decodificator de secvenţe. Se generează secvenţe care validează acţiunile asupra elementului funcţional (UE).

Generator

de tact CLK

Calcul Calcul adresă Calcul adresă Calcul adresă

adresă de salt următoare de oprire

(condiţii de (condiţii (condiţii de

întrerupere) următoare) oprire)

Adresă Load Numărare Oprire

(Salt) UE

Numărător de secvenţă

Decodificator Calcul

de secvenţe acţiuni UE

CLK

b. Generatorul de secvenţe este realizat cu un registru de deplasare (decalaj) în care va circula un bit de 1. Fiecărei stări îi corespunde un bit din registrul de deplasare. Poziţia bitului de 1 semnalizează o anumită secvenţă. Pentru a obţine starea următoare registrul va fi decalat cu o poziţie sau va fi decalat în cazul saltului. Avantajul acestei variante constă în eliminarea decodificatorului de secvenţe.

În fiecare secvenţă se realizează o acţiune sau un grup de acţiuni. O acţiune poate să necesite mai multe etape. Dirijarea în cadrul secvenţei se realizează cu ajutorul generatorului de tact.

Variantele a şi b de UC cablate au dezavantajul că o modificare a funcţionării presupune o modificare a secvenţei de lucru, deci o modificare a cablajului.

2) UC microprogramate

Generatorul de secvenţe trebuie să aibă exact aceleaşi funcţii ca şi în cazul UC cablate.

Generator

de tact CLK

Calcul adresă Calcul adresă Calcul adresă

de salt următoare de oprire

(condiţii de (condiţii (condiţii de

CLK întrerupere) următoare) oprire)

Adresă Load (Salt) Numărare Oprire

Registru de microinstrucţiune UE

Registru de adresă microprogram

Adresă Calcul

Memorie microprogram acţiuni UE

Adresă nouă Acţiuni CLK

La acest mod de realizare a UC se câştigă în fiabilitate deoarece se execută o singură operaţie într-o secvenţă, dar se pierde în viteză. Tactul acţionează asupra registrului (numărătorului) de microprogram.

3.4.1. Principii de comandă a sistemelor secvenţiale sincrone

Sistemele secvenţiale sincrone îşi modifică ieşirea în funcţie de intrare doar în prezenţa unui semnal de tact.

Funcţii logice de comandă. Tabele de excitaţie

Generatorul de tact furnizează un semnal de tact de bază, care provine de la un oscilator şi este un semnal periodic de durată şi perioadă constantă. Cu ajutorul semnalului de tact se vor genera toate semnalele de comandă necesare unui sistem secvenţial sincron.

În sistemele cablate, în cadrul unei secvenţe se pot efectua mai multe operaţii. Din acest motiv este necesară dirijarea perioadei tactului pentru a stabili o succesiune a diferitelor acţiuni. Pot să apară următoarele situaţii:

Tact suprapus

T

CLK₁

CLK₂

CLK₃

Tact adiacent

CLK₁

CLK₂

CLK₃

Tact neadiacent

CLK₁

CLK₂

CLK₃

Sistemele secvenţiale sincrone se comandă prin funcţii care conţin unul dintre semnalele de tact CLK_i, o stare a circuitului şi un semnal extern. Toate funcţiile de comandă care acţionează asupra elementelor din unitatea de execuţie UE vor conţine obligatoriu unul dintre semnalele de tact în cadrul expresiei funcţiei (validează o acţiune).

Funcţiile logice de comandă nu ţin cont de natura elementului fizic utilizat. După alegerea elementelor fizice se vor grupa funcţiile de comandă într-un tabel de excitaţie. Tabelul de excitaţie conţine:

- numele elementului circuitului;

- tipul elementului;

- intrările elementului;

- modul de comandă a intrărilor;

- funcţia logică corespunzătoare fiecărei intrări, scrisă sub formă simbolică.

3.4.2. Hazardul în funcţionarea sistemelor secvenţiale sincrone

Hazardul reprezintă apariţia unei modificări neprevăzute şi nedorite a unei stări a sistemului secvenţial sincron.

Hazardul poate fi:

- static – datorat propagărilor pe căi diferite a semnalelor; se manifestă prin comutări fără semnificaţie logică;

- dinamic – datorat proceselor asincrone pe intrări; se manifestă prin comutări fără semnificaţie logică.

Cauzele apariţiei pot fi:

- semnale parazite la funcţiile de excitaţie;

- nerespectarea parametrilor dinamici;

- durata insuficientă a impulsului de comandă.

Metodele de evitare a hazardului:

1) Sincronizarea intrărilor asincrone

semnal

asincron

extern

CLK

t_setup t_hold

Exemplu. Se consideră un numărător N care face o incrementare +1 la tactul CLK şi un semnal extern E. Incrementarea se face la CLK × E.

E N

CLK +1

E

CLK

CLK × E

Se poate ca semnalul CLK × E să aibă o durată foarte scurtă care va provoca o funcţionare greşită a numărătorului N. Se va face o sincronizare a semnalului asincron E cu ajutorul unui bistabil.

E E_s +1

CBB CLK₂

CLK₁

Dacă există mai multe semnale asincrone, pentru realizarea sincronizării se utilizează registre.

2) Automodificarea unui circuit secvenţial

Poate să apară în situaţii ca şi următoarea:

f = s × CLK₁ × CLK₂ × Q₁ × Q₂

în cazul în care bistabilul al doilea, Q₂, va comuta în 0.

D Q₂

CLK₂

s

CLK₂

s × CLK₁ × Q₁ × Q₂ durată foarte scurtă, neutilizabilă

Q₂

Se face sincronizarea pentru Q₂.

Q₁ D Q₂

s CLK₂

CLK₂

s × Q₁ × Q₂

Q₂

3) Probleme datorate decalajului de tact (defazarea tactului)

Dacă la CLK₂ × s × Q₁ × Q₂ avem Q₃ ® 1 şi la CLK₂ × s × Q₁ avem Q₂ ® 0

Dacă CLK₂ care se aplică bistabilului 2 este în avans faţă de CLK₂ aplicat bistabilului 3, s × Q₁ × Q₂ ® 0 prea repede şi nu se respectă t_hold pentru bistabilul 3, deci Q₃ nu va ® 1.

J₂ Q₂ J₃ Q₃

CLK₂

Q₁ CLK CLK

s K₂ K₃

CLK₂ × Q₁

Q₂

s × CLK₂ × Q₁

t_setup t_hold

Pentru rezolvarea problemei este necesară aplicarea unui alt tact CLK₃.

4) Probleme datorate frecvenţei maxime a tactului

Circuitele MSI au specificată în catalog frecvenţa maximă de lucru, care este de obicei valoarea tipică sau medie. Datorită CLC care se interpun creşte timpul de propagare (se adaugă la timpul de propagare prin CLS, timpul de propagare prin CLC şi timpul de setup) şi astfel scade frecvenţa maximă a tactului. Proiectarea trebuie făcută încât să se introducă cel mult 2 nivele de CLC între CLS.

5) Probleme legate de iniţializare şi blocare

Orice sistem secvenţial care conţine elemente de memorie trebuie prevăzut cu o logică de iniţializare la punerea sub tensiune. Altfel elementele de memorie pot să se găsească în orice stare şi succesiunea de stări nu urmează cursul firesc proiectat.

Deoarece nu toate stările sunt folosite trebuie să se introducă o logică de autoiniţializare, care are ca scop aducerea circuitului secvenţial în secvenţa normală de lucru.

3.4.3. Perturbaţii datorate structurii electrice

Perturbaţiile pot fi de natură electrică, magnetică sau electromagnetică.

a. Perturbaţiile mediului înconjurător se elimină prin ecranare (câmpuri electrice şi magnetice) şi prin filtre de reţea (câmpul electromagnetic).

b. Efectele perturbatoare introduse de sursa de alimentare (în condiţiile în care poarta logică se asimilează cu un generator de tensiune cu rezistenţă internă şi cu ieşirea având un salt de la 0 la 5V, care determină un curent pe linia de conexiune şi prin linia de masă) se datorează:

- zgomotelor de pe liniile de masă – în cazul în care punerea la masă este incorectă (nu este aproape de porţile de emisie şi de recepţie) se generează curenţi paraziţi care se propagă pe linie şi pot produce impulsuri de tensiune parazite, care la rândul lor pot provoca răspunsuri false la ieşirile circuitelor logice;

- variaţiilor de curent continuu care apar la trecerea dintr-o stare logică în alta.

Pentru eliminarea acestor probleme se cuplează la masă firele de legătură şi cablurile coaxiale cât mai aproape de porţile de emisie şi recepţie ale liniei. Decuplarea tensiunii de alimentare a porţilor de emisie şi de recepţie ale liniilor se realizează cu condensatoare pentru înaltă frecvenţă şi pentru joasă frecvenţă, montate cât mai aproape de circuitul logic. Pentru o decuplare şi mai eficientă se folosesc şi inductanţe pentru eliminarea oscilaţiilor.

c. Diafonia reprezintă toate fenomenele de cuplaj electromagnetic între semnalele de pe liniile de legătură, care dacă interacţionează produc semnale parazite.

O bucată de conductor poate fi privită ca şi o antenă slabă, dacă nu are o lungime de cel puţin ¼ l. Din acest motiv firele de legătură pot fi privite ca antene de recepţie pentru zgomote. Diafonia poate fi privită ca şi transmisie radio în care un conductor emite şi celălalt recepţionează. Din acest motiv 2 fire de legătură paralele alăturate pot produce diafonie. Eliminare se realizează prin introducerea unui traseu de masă între liniile de legătură. Ideală ar fi utilizarea firelor încrucişate (fir de legătură cu fir de masă în jurul lui).

d. Propagarea şi reflexiile pe liniile de transmisie. Liniile de transmisie sunt caracterizate de impedanţă. Aceasta reprezintă raportul dintre tensiunea şi curentul semnalelor de înaltă frecvenţă care parcurg linia. Dacă terminaţia liniei este o rezistenţă egală cu impedanţa lui nu apar probleme de propagare. Altfel pot apărea reflexii, datorită neechilibrării liniei de transmisie, care se suprapun peste semnalul iniţial.

Dacă liniile de transmisie sunt foarte lungi timpul de propagare poate ajunge egal sau mai mare decât fronturile şi atunci pot să apară reflexii.

Aceste probleme sunt deosebit de importante pentru semnalele de tact, de aceea se va urmări cu atenţie lungimea şi terminaţia firelor de pe aceste semnale (altfel circuitul poate într-un singur tact să parcurgă mai multe stări).

Curs 12

CAPITOLUL IV

PROIECTAREA SISTEMELOR NUMERICE CU DISPOZITIVE PROGRAMABILE

4.1. Metodologii generale de proiectare a sistemelor numerice

4.1.1. Proiectarea clasică

Să recapitulăm etapele fluxului de proiectare în varianta clasică.

- se începe cu o specificaţie;

- se construieşte o diagramă bloc;

- se separă secţiunile organigramei, după care se detaliază fiecare până când se atinge nivelul corect al designului logic;

- se integrează piesele; în caz că există un produs software dezvoltat anume pentru gestionarea sistemului, acesta este momentul când se va utiliza;

- se creează prototipul, care este depanat şi corectat cu ajutorul softului; adeseori, prototipul nu funcţionează la viteza proiectată şi trebuie reexaminat pentru diverse corecţii (de exemplu gâtuiri - bottlenecks);

- se realizează fizic sistemul pe placă (PCB - Printed Circuit Board); şi aici apar de multe ori corecţii care trebuie efectuate, aspecte impuse de condiţiile fizice de realizare a PCB-ului.

Deci revenirile multiple în procesul de proiectare clasică constituie regula, nu excepţia. Procesul de proiectare este astfel costisitor din punct de vedere al timpului (circa 6-12 luni pentru sisteme de 500-1000 de circuite integrate (capsule)).

4.1.2. Proiectarea cu dispozitive programabile

Noul scenariu de proiectare, cu dispozitive programabile, este următorul:

- se porneşte şi aici tot de la specificaţie;

- sistemul este apoi partiţionat în blocuri mari (memorii, microprocesoare, dispozitive logice programabile, FPGA-uri sau CPLD-uri şi logică de interfaţare);

- se formulează o descriere de nivel înalt a sistemului, folosindu-se un editor schematic sau un limbaj de descriere hardware abstract (de exemplu, VHDL sau ABEL);

- întregul sistem este simulat - înlocuindu-se astfel vechea fază de prototip;

- se creează lista de componente (netlist) a sistemului;

- netlista este folosită la realizarea PCB-ului; în timpul realizării fizice a PCB-ului, simularea mai este rafinată.

În acest tip de proiectare cele mai multe modificări, dacă nu chiar toate, apar în software, în PLD-uri sau în FPGA, nu în interconexiuni sau în componente secundare.

Dacă designul a fost bine conceput, el poate fi reproiectat cu matrici de porţi, pentru a maximiza profitul la producţia de serie mare.

Folosirea intensivă a circuitelor FPGA este o modalitate foarte eficientă de proiectare a sistemelor numerice. FPGA-urile permit proceduri de realizare fizică foarte rapide şi modificări chiar mai rapide ale designului, cu condiţia să fie corect folosite. Cheia succesului lor este time-to-market-ul (timpul de la conceperea abstractă a unui proiect până la realizarea sa efectivă) foarte rapid.

4.2. Definiţia şi structura unui circuit FPGA

4.2.1. Completitudine funcţională

Un concept de bază în înţelegerea FPGA-urilor este completitudinea funcţională. Se ştie că orice funcţie poate fi realizată pornind de la o sumă de produse. Dacă un singur tip de poartă logică este capabilă de a forma o sumă de produse, atunci spunem că are proprietatea de completitudine funcţională. Asta înseamnă că orice funcţie booleană poate fi realizată folosindu-se numai acel tip de poartă logică. În consecinţă este avantajos să avem multe porţi de tipul respectiv.

Calităţile esenţiale pentru completitudinea funcţională sunt:

- cu ajutorul porţii respective să poată fi construită funcţia logică ŞI;

- cu ajutorul porţii respective să poată fi construită funcţia logică NU

sau:

- cu ajutorul porţii respective să poată fi construită funcţia logică SAU;

- cu ajutorul porţii respective să poată fi construită funcţia logică NU.

Nu este nevoie să impunem realizarea simultană a funcţiilor ŞI şi SAU, deoarece, dacă se poate realiza funcţia NU, atunci, folosind teoremele lui De Morgan, se poate obţine şi funcţia care lipseşte.

4.2.2. Funcţii universale

Funcţiile universale sau generatoarele de funcţii sunt blocuri logice care pot fi configurate astfel încât să realizeze orice funcţie logică de intrările blocului. Există mai multe tipuri de astfel de blocuri logice. Cele mai cunoscute sunt memoriile (ROM, RAM, PROM, EPROM şi EEPROM) şi multiplexoarele. Toate aceste blocuri pot realiza funcţii, formând tabelele lor de adevăr. FPGA-urile sunt adeseori construite pe baza unor blocuri constructive care sunt funcţii universale.

Să luăm exemplul unui multiplexor 4:1. Ecuaţia ieşirii este următoarea:

S1	S0	DATAOUT
0	0	D0
0	1	D1
1	0	D2
1	1	D3

DATAOUT = S₁×S₀×D₀ + S₁×S₀×D₁ + S₁×S₀×D₂ + S₁×S₀×D₃

Examinând fie tabelul de adevăr al multiplexorului, fie ecuaţia ieşirii, obţinem:

- dacă D₀ = D₁ = D₂ = 0 şi D₃ = 1, atunci funcţia DATAOUT va fi S₁ × S₀, adică ŞI logic;

- dacă D₀ = 0 şi D₁ = D₂ = D₃ = 1, obţinem DATAOUT = S₁+S₀, adică SAU logic;

- dacă D₀ = D₂ = 1 şi D₁ = D₃ = 0, obţinem DATAOUT = S₀, adică NU logic.

Aceste observaţii arată că multiplexorul este complet funcţional. El este şi universal pentru că poate forma orice funcţie de cele două variabile de intrare S₀ şi S₁ (selecţiile) prin setarea valorilor lui D din tabelul de adevăr la 0 sau la 1 logic.

Analog, un multiplexor 8:1 poate realiza orice funcţie de 3 variabile de intrare, iar un multiplexor 16:1 poate realiza orice funcţie de 4 variabile etc.

O celulă care are proprietatea de completitudine funcţională poate realiza orice funcţie logică combinaţională folosind una sau mai multe copii ale sale.

O funcţie logică universală poate face acelaşi lucru, dar s-ar putea să necesite mai puţine celule. Aici presupunem că celula universală are suficiente intrări pentru a fi eficientă, ceea ce poate să nu fie întotdeauna adevărat. Unele FPGA-uri folosesc ca blocuri constructive celule universale, altele folosesc celule funcţional complete.

4.2.3. Definiţia circuitului FPGA

Un FPGA este o colecţie de elemente logice cu completitudine funcţională sau universale plasate într-o reţea de interconectare.

Unele FPGA-uri arată ca nişte matrici de celule bidimensionale, cu canale de interconectare orizontale şi verticale între celule. Altele arată ca nişte porţi logice împreună cu matrici programabile, cu reacţie inversă, similare PLD-urilor obişnuite. Pentru a face distincţia între ele, primele au fost numite FPGA-uri, iar celelalte - CPLD-uri (Complex Programmable Logic Device); sau arhitecturi cu canale de rutare şi respectiv arhitecturi foldback.

Arhitecturi FPGA şi CPLD (foldback)

Să luăm un exemplu de arhitectură FPGA pe care să o construim pe bază de multiplexoare. Pornim de la un multiplexor de tip 8:1.

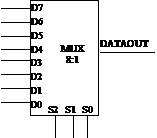
Dacă FPGA-ul ar fi construit numai pe bază de multiplexoare 8:1, bistabilele ar fi greu de implementat şi preţul realizării lor ar fi mult prea mare. O practică uzuală constă în a face celula universală (sau funcţional completă) să aibă ieşirea legată direct la intrarea unui bistabil D, care basculează pe front, obţinându-se astfel o celulă hibridă, care conţine şi un bistabil. Aici apare în continuare o problemă: toate funcţiile combinaţionale sunt obligate să folosească şi bistabile D.

Multiplexor cu ieşire prin registru

Soluţia cea mai folosită constă în a adăuga încă un multiplexor în celulă, permiţând multiplexorului să conducă direct intrarea D a bistabilului sau să-l ocolească pentru a "ieşi" în exterior. Acum, structura blocului constructiv este rezonabilă din multe puncte de vedere. El poate forma orice funcţie combinaţională de trei variabile şi poate, de asemenea, forma funcţii secvenţiale realizate cu bistabile D. În figură se prezintă celula finală, împreună cu simbolul ei. De notat că intrările de date nu sunt scoase în afara celulei. Numai ceasul şi 4 intrări de selecţie sunt intrări pentru formarea funcţiilor logice, ceea ce reduce considerabil numărul de conexiuni externe necesare implementării de funcţii logice.

Celula de bază a unui FPGA cu blocuri logice universale

Să vedem acum cum pot fi interconectate aceste celule. Potrivit celor expuse anterior există două moduri fundamentale de a realiza interconectarea: prin canale de rutare sau prin matrice programabilă de tip foldback, cu reacţie inversă.

Arhitectură FPGA cu canale de rutare a semnalelor inter-celulare

Semnalele intră în structura din figură prin buffere de intrare, ajungând la liniile verticale şi orizontale. În toate punctele de intersecţie a unei linii orizontale cu una verticală se poate realiza o conexiune. Valorile logice de pe liniile de intrare (de date) ale multiplexoarelor sunt setate prin intermediul unor circuite de programare a FPGA-ului. Funcţia fiecărei celule este deci programată intern, iar ieşirea este rutată înspre mai multe linii verticale şi orizontale. Semnalele de la ieşirea unei celule pot fi rutate la intrările altor celule sau la ieşirile circuitului FPGA, ieşiri care sunt realizate prin buffere de ieşire.

Arhitectură CPLD de tip foldback, cu reacţie inversă

În cazul arhitecturii CPLD, ieşirile tuturor celulelor sunt rerutate în interiorul matricii (reacţie inversă) către intrările tuturor celorlalte celule. Şi aici se presupune că circuitele de programare (configurare) a celulelor nu apar în figură. Funcţiile simple sunt realizate în celule, iar pentru cele mai complexe se folosesc căile de reacţie inversă. În figură apar puţine celule în structura foldback-ului, dar în realitate, cu tehnologia de azi, numărul acestor celule poate atinge câteva sute.

Arhitecturile prezentate sunt relativ simple şi totuşi există un anumit număr de probleme care apar:

- Câţi pini de intrare, ieşire şi bidirecţionali sunt necesari?

- Este oare bine să avem pini de clock (tact) dedicaţi?

- Care este numărul corect de linii de interconectare verticale şi orizontale necesare pentru a evita congestia?

- Este bine oare să se divizeze liniile de interconectare în mai multe sub-segmente, în vederea evitării blocării unei căi?

La toate aceste probleme trebuie să se răspundă în funcţie de arhitectura specifică folosită (firma producătoare, tehnologia de realizare a FPGA-ului, structura celulei etc.).

Curs 13

4.3. Instrumentele software de susţinere a proiectării cu FPGA-uri

4.3.1. Introducere

Arhitecturile prezentate anterior erau alcătuite din celule logice identice plasate într-o reţea de conexiuni posibile. Folosirea acestor arhitecturi necesită translatarea funcţiei dorite de către proiectant în conexiunile intra şi intercelulare necesare obţinerii designului final.

Există două funcţii principale pe care trebuie să le realizeze instrumentele software de susţinere a proiectării cu circuite FPGA:

1) să convertească funcţiile designului în funcţiile realizabile de către FPGA. Această funcţie se numeşte translatare (alteori compilare sau fitting - potrivire).

2) să verifice dacă designul translatat este corect. Această funcţie se numeşte verificare şi poate fi realizată cu softul de verificare a designului şi de simulare logică.

Ambele funcţii operează cu o versiune a designului numită netlist (listă de conexiuni şi componente) asupra căreia se pot face investigaţii, deoarece este o reprezentare comună a circuitului.

4.3.2. Problema translatării

Paşii care trebuie parcurşi în cursul procesului de translatare sunt în general următorii:

- se verifică dacă numărul pinilor de intrare/ieşire ai FPGA-ului este mai mare decât numărul pinilor necesari în design;

- se verifică dacă există suficiente celule în FPGA pentru a acoperi numărul de porţi logice din design;

- se caută în design grupuri de componente al căror număr de intrări şi de ieşiri este egal cu cel al celulei de bază din FPGA;

- se aleg prima dată grupurile cele mai mari care pot fi formate (de exemplu porţile cu mai mult de trei intrări au nevoie de două sau mai multe celule).

Instrumentul software utilizează un set de reguli pentru substituţiile de funcţii. La nivelul cel mai simplu, el are nevoie de un set de substituţii pentru porţile din design care să fie mapate în celule din FPGA. În continuare, el are nevoie de o strategie pentru a utiliza optimal regulile de substituţie.

Procesul de translatare este alcătuit din trei etape esenţiale:

- maparea tehnologică (inclusiv optimizarea);

- plasarea;

- rutarea.

O operaţiune importantă este eliminarea părţilor redundante din design - altfel cele mai multe designuri nu pot fi implementate în FPGA.

Exemplu: Dacă în design apare un numărător pe 4 biţi din care se folosesc efectiv numai cei 2 biţi mai puţin semnificativi, softul va "sparge" implementarea numărătorului pe 4 biţi şi va realiza doar implementarea unui numărător pe 2 biţi, restul logicii iniţiale fiind de prisos în acest caz.

4.3.3. Optimizarea netlist-ei

Este o etapă esenţială a procesului de proiectare automată cu FPGA-uri. Se folosesc de obicei metodele clasice: diagrame Karnaugh, teoremele algebrei booleene etc.

Această optimizare este de fapt minimizarea designului după translatarea sa într-o netlistă. Netlista este un fişier text care conţine pur şi simplu funcţiile logice din design şi conexiunile lor de intrare şi de ieşire. Acelaşi format poate fi folosit la orice nivel de reprezentare. Un exemplu de netlistă:

*

NETSTART

*

OUT3 DFF I(OUT3_D, CLOCK) O(OUT3, N_ OUT3)

OUT3_D AN2 I(A1, N2O_1) O(OUT3_D)

B2O_1 INV I(A2) O(N2O_1)

OUT2_D OR2 I(N21_2, N21_4) O(OUT2_D)

OUT2 DFF I(OUT2_D, CLOCK) O(OUT2, N_OUT2)

B21_4 AN2 I(N21_3, A4) O(N21_4)

B21_2 AN2 I(N21_1, A2) O(N21_2)

B21_1 INV I(A1) O(N21_1)

B21_3 INV I(A3) O(N21_3)

OUT1 DFF I(OUT1_D, CLOCK) O(OUT1, N_OUT1)

B22_1 AN2 I(A1, A2) O(N22_1)

B22_2 AN2 I(A3, A4) O(N22_2)

OUT1_D OR2 I(N22_1, N22_2) O(OUT1_D)

*

NETEND

*

NETIN A1, A2, A3, A4, CLOCK

NETOUT OUT1, OUT2, OUT3

*

Exemplu de netlistă

În această netlistă, DFF înseamnă bistabil D (D flip-flop), AN înseamnă poartă ŞI, INV înseamnă poartă NU, iar OR înseamnă poartă SAU.

Acesta este nivelul la care se fac substituţiile; există sute de reguli. Exemplu: Se elimină porţile logice din design ale căror ieşiri nu sunt folosite. Astfel se pot combina porţile care realizează funcţii identice, se pot elimina bistabile etc. Procesul de "convertire" a componentelor logice din design în componente logice implementabile de către celulele de bază din FPGA se numeşte mapare tehnologică.

4.3.4. Plasarea

Este procesul de amplasare fizică a componentelor logice în celulele din FPGA. În principiu se urmăreşte amplasarea funcţiilor logice adiacente în celule alăturate (dacă un modul logic are ca intrări ieşirile altui modul, cele două module vor fi adiacente). Criteriul critic de plasare este următorul: să se poată face legăturile cu celelalte celule.

4.3.5. Rutarea

Presupunând că s-a reuşit efectuarea unei plasări adecvate a componentelor logice în celulele din FPGA, pasul următor este interconectarea acestora. La început, netlista este inspectată, urmărindu-se informaţiile de interconectare din ea. Apoi se inspectează plasarea existentă în acest moment. Se consideră că dacă o linie metalică de interconexiune are ataşat un semnal de ieşire şi celălalt capăt al său este conectat la intrarea unei alte celule, atunci linia este folosită (consumată). Pe măsură ce procesul de interconectare avansează, liniile devin ocupate şi poate să apară congestia. În această situaţie, softul va reface plasarea, proces numit re-rutare.

Rezultatul plasării şi rutării este un fişier care descrie designul originar în termenii celulelor FPGA-ului. Acest fişier conţine descrierea asignării poziţiilor celulelor şi interconexiunilor dintre celule pentru reţeaua de tip FPGA sau CPLD (foldback). În final fişierul este translatat într-o hartă de biţi care poate fi transmisă unui programator de dispozitive care configurează FPGA-ul.

Se vede deci că un instrument software de rutare a semnelor din FPGA este vital pentru exploatarea posibilităţilor oferite de aceste circuite.

4.3.6. Căi critice

Problemele care apar în proiectarea cu FPGA-uri sunt în special probleme de temporizare. De exemplu: un semnal trebuie să intre în FPGA, să ia parte la implementarea unei funcţii logice şi apoi să iasă imediat pentru a participa la alte operaţii în afara FPGA-ului (aşa se întâmplă deseori la sistemele cu microprocesoare, la decodificatoare, la comparatoare rapide etc.). Alteori, toate bistabilele dintr-un registru de deplasare sau numărător trebuie să fie plasate în celule adiacente din FPGA, pentru a garanta sosirea aproape simultană a semnalului de tact la aceste celule.

Căile critice complică plasarea şi rutarea pentru că sporesc numărul de constrângeri adiţionale. De obicei se plasează întâi celulele aflate pe căi critice, apoi restul celulelor din design. În continuare se rutează în mod similar: întâi celulele aflate pe căi critice, apoi restul celulelor din design. În acest fel rămân mai puţine posibilităţi pentru plasarea şi rutarea restului designului.

Se recomandă să se păstreze la un nivel minim căile critice, pentru că altfel sesiunile de plasare şi rutare devin mult mai lungi.

4.3.7. Verificarea designului

Cele mai simple instrumente de verificare a designului sunt programe care examinează netlista transformată şi analizează proprietăţile ordinare ale designului final. Iată câteva exemple de verificări efectuate:

- se izolează ieşirea unei celule şi se numără la intrarea câtor altor celule este transmis acel semnal. Fiecare celulă în care intră semnalul contribuie la o sarcină cumulativă a acestuia şi este posibil ca atunci programul să intervină, distribuind sarcina respectivă la mai multe celule de ieşire identice;

- se caută intrări lăsate neconectate ale celulelor, care creează probleme de zgomote;

- se caută ieşiri care nu sunt three-state şi sunt totuşi legate împreună.

Uneori verificarea se face în etapa de translatare, alteori în etapa de simulare.

4.3.8. Simularea logică

Acesta este instrumentul de bază pentru verificarea funcţionalităţii şi performanţelor temporale ale unui design cu FPGA. În orice tip de simulare, se creează un model al reţelei logice căruia i se aplică un model al intrărilor (numite stimuli) în vederea obţinerii unui model al ieşirilor (numite răspunsuri). O proprietate fundamentală a simulării este următoarea: ea permite observarea răspunsurilor logice interne, când aceste răspunsuri s-ar putea să nu fie observabile pe pinii de ieşire.

Există mai multe tipuri diferite de simulare:

4.3.8.1. Simularea funcţională

În acest tip de simulare se modelează celulele logice, care sunt combinate cu un model al intrărilor binare (tensiuni), generându-se un model relativ de răspunsuri (tot tensiuni).

Avantaje:

- generează rapid rezultatele;

- modelul este simplu.

Dezavantajul principal:

- nu oferă informaţii despre temporizare, ci numai relaţii relative între semnale.

4.3.8.2. Simularea temporală digitală

În acest tip de simulare se creează un model al întregului design, interconectându-se modelele celulelor, asociindu-se în plus un element adiţional la ieşirea modelului fiecărei celule: un bloc de întârziere.

Blocul de întârziere al unei celule este compus din trei factori:

1) întârzierea introdusă de celulă în sine, în absenţa oricărei conexiuni externe. Şi această întârziere este de fapt alcătuită din două întârzieri:

- întârzierea pentru tranziţia din "1" logic în "0" logic;

- întârzierea pentru tranziţia din "0" logic în "1" logic.

Specificarea acestor două valori în data sheet-ul circuitului integrat FPGA este opţională.

2) întârzierea asociată capacităţii de rutare a firului de metal care uneşte două celule;

3) întârzierea dată de suma impedanţelor de intrare ale celulelor comandate.

Uneori, întârzierile de la punctele 2) şi 3) sunt luate împreună. Această simulare este mult mai complexă. Nu vom intra în detaliile realizării efective a acestui tip de simulare (modul de realizare a modelelor, planificatorul de evenimente etc.)

4.3.8.3. Simularea defectelor

În acest tip de simulare se folosesc tehnici speciale pentru a se obţine un "scor" (numit grad de defecte) pentru design şi stimulii aplicaţi. Se testează fiecare aspect al designului conform standardelor industriale.

Ideea este de a crea probleme artificiale ("defecte") şi de a urmări dacă răspunsurile diferă de cele obţinute în cazul normal, corect. Simularea fundamentală constă în menţinerea ieşirilor unor celule la 0 sau la 1 logic, în timp ce se aplică stimulii. Acest proces nu este efectuat pentru toate nodurile deodată, dar poate fi realizat pentru mai multe noduri simultan, dacă acestea sunt suficient de independente unul faţă de celălalt.

Această simulare necesită multiple rulări pentru a calcula un grad de defecte şi de aceea este o mare consumatoare de timp.

În general, pentru FPGA-uri se foloseşte mai ales simularea temporală, pentru PLD-uri - simularea funcţională, iar pentru ASIC-uri mari - simularea de defecte.

4.3.9. Evaluarea

Simulatorul are o bibliotecă de funcţii în care fiecare intrare are ataşată o rutină care evaluează un tabel de adevăr. Spre deosebire de un tabel de adevăr normal, intrările într-un tabel de adevăr de simulator reflectă mai realist condiţiile electrice (de exemplu: ieşiri three-state, stări necunoscute etc. - vezi figura 9).

Æ = ZERO

1 = HIGH

* = NECUNOSCUT

3 = TRI-STATE

# = NEDETERMINAT

ŞI-NU	Æ	1	*	3	#
Æ	1	1	1	1	1
1	1	Æ	*	#	#
*	1	*	*	#	#
3	1	#	#	#	#
#	1	#	#	#	#

A) Modelul logic

B) Modelul cu o întârziere adăugată

Modelul de simulare al unei porţi ŞI-NU

O poartă ŞI-NU normală are doar patru intrări în tabelul de adevăr. Acest tabel de adevăr are 25 de intrări deoarece intrările porţii pot avea 5 valori posibile per intrare. În figura 9, intrările pot fi valorile logice 0 şi 1, dar şi necunoscute, three-state sau nedeterminate. Condiţia necunoscută poate să apară într-o situaţie reală dacă intrarea porţii provine de la un bistabil a cărui ieşire Q este necunoscută (de exemplu la punerea sub tensiune, start-up). Intrarea three-state poate să apară la o intrare dacă aceasta provine de la ieşirea unei porţi three-state de pe un nivel logic anterior. Condiţia nedeterminată a intrării poate să apară dacă două buffere three-state comandă acelaşi nod cu un nod care realizează un ŞI cablat atunci când un buffer eliberează comanda sa în timp ce celălalt buffer asertează.

Cu cât număul de stări creşte, cu atât creşte şi acurateţea simulării, dar cu preţul unui consum sporit de timp de rulare.

4.3.10. Modelarea

Simularea performantă include folosirea unor limbaje de modelare speciale, foarte eficiente, numite BLM (Behavioral Language Models). Acestea sunt modele de evaluare care generează răspunsuri de ieşire corecte la stimuli de intrare daţi. Un BLM este alcătuit de fapt din proceduri scrise pentru a reacţiona corect la un stimul, dar nu conţine vreun model de poartă anume. Cel mai simplu BLM este cel al unui bistabil D. Codul este scris în VHDL, care a fost optimizat pentru portabilitate pe multe sisteme de proiectare asistată de calculator.

EDGE_TRIGGERED_D: block (CLK = ‘1’ and not CLK ‘STABLE or CLR = ‘1’)

begin

Q <= guarded ‘0’ when CLR = 1; else

D when CLK = ‘1’ and not CLK ‘STABLE else

Q;

end block EDGE_TRIGGERED_D;

Modelul unui bistabil în VHDL

Abordarea BLM permite verificări interne pentru violări de timpi de setup şi de hold în interiorul rutinei care evaluează operaţia logică respectivă.

Acelaşi bistabil D poate fi modelat şi în versiunea cu porţi (deci bistabilul e văzut ca un circuit de şase porţi ŞI-NU, cu reacţie). Această versiune necesită ca modelului să-i fie ataşată o funcţie externă, pentru a răspunde necesităţilor de verificare a timpilor de setup şi de hold ai modelului.

BLM evaluează rapid, dar nu arată operaţiile interne - rămâne ca o cutie neagră.

Versiunea cu porţi face o disecţie completă a operaţiilor modelului, necesitând un timp de simulare mai mare. În plus, ea permite o evaluare completă a gradului de defecte.

De regulă, funcţiile mari sunt modelate şi simulate cu BLM, iar cele mai mici - cu ajutorul modelelor cu porţi.

4.3.11. Biblioteci

Simulatoarele sunt livrate cu biblioteci de modele de simulare, cu blocurile constructive necesare gestionării celei mai mari părţi a designurilor. Aceste biblioteci includ porţi elementare, bistabile, intrări, ieşiri şi mai multe funcţii adiţionale.

Aici se pot modifica întârzierile nodurilor interne, se pot rula subrutine ale stimulilor etc.

4.3.12. Back Annotation

Procesul de alterare a întârzierilor nodurilor interne se numeşte back annotation, noţiune esenţială în proiectarea cu FPGA. Modelul de simulare iniţial era pur şi simplu netlista designului. Înainte de plasarea şi rutarea designului, întârzierile sunt necunoscute (între oricare două puncte din interiorul FPGA-ului). După plasarea şi rutarea designului, întârzierile devin precizate. Produsul software calculează întârzierile interne folosind legile circuitului electric, lungimea firelor metalice, constantele dielectrice şi alţi parametri.

Folosind aceste întârzieri, softul alcătuieşte o netlistă cu întârzieri notate nod cu nod, modificând netlista originară. Acesta este procesul de back annotation. Simularea pe baza acestei noi netliste este mult mai precisă, detectând puncte critice care nu au cum să fie observate din lumea externă.

4.3.13. Procesul de proiectare cu FPGA

În concluzie, putem sintetiza paşii procesului de proiectare cu FPGA:

Diagrama procesului de proiectare cu FPGA

Recapitulând, putem distinge următorii paşi ai acestui proces:

1. Se introduce designul folosind un editor schematic (schematic capture sau ecuaţii);

2. Rezultă o netlistă care descrie designul;

3. Netlista este transmisă simulatorului pentru verificare funcţională (pentru a vedea dacă au fost capturate funcţiile corecte);

4. Urmează procesul de compilare: plasare şi rutare;

5. După compilare, softul de analiză extrage întârzierile date de interconectarea celulelor şi realizează procesul de back annotation al netlistei;

6. Dacă simularea noii netliste satisface condiţiile, atunci totul este în regulă şi se face inscripţionarea fizică a circuitului FPGA (programarea). În caz contrar, se reface simularea până la obţinerea versiunii definitive corecte.