MINIMIZAREA FUNCTIILOR LOGICE CU AJUTORUL CIRCUITELOR NAND SI REPREZENTAREA FORMEI
1. Scopul lucrarii.
Se studiaza minimizarea functiilor logice cu ajutorul metodei diagramelor Karnaugh si se prezinta modul in care se poate determina direct din aceste diagrame forma minimizata a functiei exprimata cu ajutorul circuitelor SI-NU (NAND).
2. Consideratii teoretice.
Minimizarea consta in trecerea unei expresii de la forma canonica la o forma elementara, deci eliminarea unor variabile din expresia functiei.
Regula de minimizare a functiilor scrise sub forma canonica P (forma canonica normal disjunctiva - f.c.n.d. ), prin diagrame Karnaugh este urmatoarea:
pentru fiecare termen P se va completa 1 in casuta corespunzatoare combinatiei respective
se grupeaza grupuri de 1 aflati in patrate adiacente, inclusiv patratele de pe laturile extreme; numarul maxim de vasute care contin 1 trebuie sa fie o putere a lui 2
din fiecare grup se elimina variabilele care isi schimba starea
se scrie forma minimizata a functiei ca suma a produselor variabilelor ramase din fiecare grup
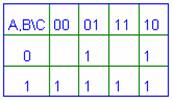
Se considera functia logica de
trei variabile definita prin tabelul de adevar din figura 1. de aici
rezulta forma canonica P a functiei: 
. Implementarea acesteia cu module NAND se afla in
figura 2.
Din diagrama Karnaugh din figura 3 se obtine forma minimizata a functiei F.
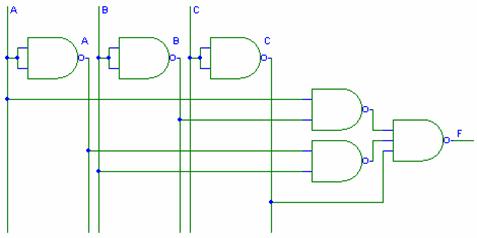
Circuitul care reprezinta solutia minimizata a functiei date realizata cu ajutorul portilor NAND este reprezentat in figura 4.
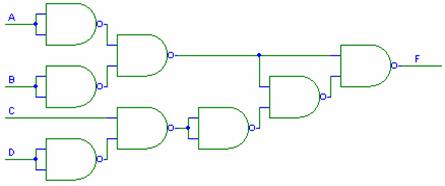
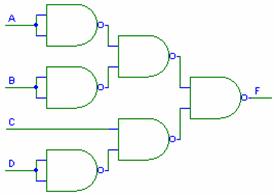
Functia logica realizata de
circuitul din figura 5 este: 
, iar implementarea acestei functii cu module NAND este
prezentata in figura 7.
Minimizarea functiilor booleene prin
metoda simbolica foloseste reprezentarea functiilor prin simbol
de marcare, permitand minimizarea sigura si a functiilor
booleene de 10 12 argumente. Simbolul de marcare este o reprezentare
numerica a functiilor booleene si deriva din reprezentarea
prin tabel de adevar.
Pentru o schema cu trei variabile
de intrate x1, x2, x3 si o singura
variabila de iesire Y, simbolul de marcare se scrie sub forma 
unde n1,, n2, n3,
marcheaza situatiile in care variabila de iesire este egala
cu 1 pentru diferite valori 0 sau 1 ale variabilelor de intrare. Numerele ni
din simbolul de marcare, scrise in cod octal se numesc numere de stare si
caracterizeaza complet starea schemei intr-o anumita situatie.
Minimizarea prin metoda simbolica se realizeaza prin intermediul listelor de adiacenta. Daca doi termeni P difera doar prin valoarea binare a unei singure variabile binare., atunci numerele de stare care corespund se numesc adiacente: in cod octal numerele diferenta de adiacenta pot fi 1, ,2, 4, 10, 20, 01, 100, 200, 400.
Primul numar de stare (se considera numerele de stare ordonate crescator in simbolul de marcare) va constitui capul primei liste de adiacente. Lista de adiacenta se formeaza din numerele de stare, adiacente cu capul de lista. Pentru a nu fi luat de mai multe ori in formarea listelor de adiacenta, fiecare numar de stare adiacent cu capul de lista se bifeaza in simbolul de marcare prin subliniere.
Primul numar de stare nebifat in simbolul de marcare va fi capul celei de a doua liste de adiacente s.a.m.d. pana la cuprinderea tuturor numerelor de stare in liste de adiacente.
In locul in care se treceau numerele de stare in simbol se trece valoarea in binar a capului de lista, fiecare bit fiind trecut in dreptul fiecarui argument. Dispar din componenta implicantului acele argumente care corespund diferentelor de adiacenta marcate in liste.
In expresia algebrica a implicantilor esentiali argumentele intra ca atare sau negate dupa cum corespund unui bit 1 sau 0 din desfasurarea capului de lista.
3. Mersul lucrarii.
Materiale si aparatura necesara.
CI: CDB-400 E, 410 E, 430 E, stand pentru circuite integrate logice.
Modul de lucru.
se va reprezenta functia de trei variabile data prin tabelul de adevar din figura 1 in doua variante forma canonica P si forma minimizata
se vor realiza schemele logice din figura 5 si figura 7 stabilindu-se pentru fiecare schema tabelul de adevar
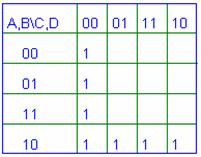
se considera functia de trei variabile data prin tabelul de adevar din figura 8; se va prezenta forma canonica P si forma minimizata; se vor implementa cele doua functii cu module NAND verificandu-se pentru fiecare schema corectitudinea functionarii
Intrebari.
Sa se minimizeze functiile date prin tabelul de adevar din figura 1 si relatia din figura 3 prin metoda simbolica
Sa se minimizeze functia: 
cu diagrame Karnaugh si prin metoda simbolica
Sa se minimizeze functia : F=ABD+ABCD+ABCD cu diagrame Karnaugh si utilizand teoremele algebrei booleene
Sa se minimizeze cu metoda Quine-McCluskey
urmatoarea functie: 
Sa se minimizeze functia: 
Sa se sa se realizeze analiza schemei logice din figura 5 aplicand regulile pentru schemele realizate cu porti inversoare.
Continutul referatului.
Rezolvarea completa a intrebarilor, prezentarea schemelor logice realizate si verificarea in cadrul lucrarii. Langa schema implementata si analizata se ataseaza tabelul de adevar.
