|
FACULTATEA DE INGINERIE AEROSPATIALA
Proiectarea pilotului automat
pentru
unghiul de atitudine longitudinala
Introducere
Descrierea aeronavei Boeing 767-400ER
Primul model B767 a intrat in productie pentru a acoperi segmentul de mijloc in transportul aerian trans- si intercontinental, oferind capacitate de transport si consum de combustibil mai mici pe rute intercontinentale si transcontinentale fata de Boeing 747. In plus, a fost gandit ca inlocuitor pentru deja vechile si neincapatoarele Boeing 707
Printre inovatiile aduse de avion se numara autorizarea pentru operatiuni Cat IIIb (aterizari pe vizibilitate aproape nula, fara altitudine de decizie, si cu o vizibilitate frontala de sub 100m).Este primul avion astfel autorizat in Statele Unite si pentru zboruri ETOPS (posibilitatea de a zbura pe distante lungi peste ocean, cu doar doua motoare). O alta inovatie este comunalitatea - instrumentele de zbor si cabina de control de pe 767 sunt identice cu cele de pe Boeing 757, permitand trecerea usoara intre cele doua modele.
Boeing 767-400ER este ultimul model 767, introdus in 1997, la comanda Delta Air Lines si Continental Airlines pentru a inlocui vechile trimotoare McDonnell Douglas DC10 si Lockheed L-1011 din dotarea flotelor lor. Avionul a fost lungit, aripile au fost lungite si ele, si varful aripilor a fost modificat pentru o aerodinamicitate crescuta. Modelul nu a fost foarte popular, avand doar 3 cumparator, cu 38 de bucati achizitionate.
Cateva detalii tehnice ale aeronavei:
Masa proprie, gol: 103.87 t
Masa maxima de serviciu autorizata la decolare (MTOW): 204.11 t
Autonomie: 5625 NM(10415 km) transpacific
Viteza croaziera: Mach 0.80(470kt, 530mph, 851 km/h la FL350)
Viteza maxima de serviciu: Mach 0.86 (493kt, 568 mph, 913 km/h la FL350)
Distanta de decolare: 9.501 ft (1896 m)
Motoare(x2): P&W PW4000-94
GE CF-80C2
Forta de propulsie: PW: 281,6 kN
GE: 282.5 kN
Cap.l Proiectarea SAS
1.l Analiza dinamicii longitudinale nereglate
Pentru analiza raspunsurilor in timp la comenzi treapta unitate si impuls se va liniariza dinamica longitudinala a avionului pentru conditiile nominale de zbor:
h = 1000 m; f/0=150m/s
Se vor lua in considerare:
-variatia de viteza de-a lungul axei longitudinale (Ox) ![]() viteza ascensionala -
viteza ascensionala - ![]() ;
;
-viteza unghiulara de tangaj -![]() ;
;
unghiul de atitudine
longitudinala-![]()
Dinamica longitudinala se poate scrie ca un sistem liniar:
x = Ax + BS, (1.1)
in care x este vectorul de stare, A este matricea de stabilitate, B este matricea de comanda, iar δ este comanda (care se va considera ca fiind bracajul de profundor δe
Relatia (1) se mai poate scrie:
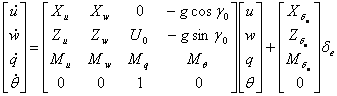 (1.2)
(1.2)
Pentru conditiile nominale de zbor matricile
![]() si
si ![]() au urmatoarele valori:
au urmatoarele valori:
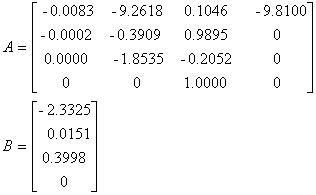 (1.3)
(1.3)
Valorile
proprii ale matricei de stabilitate ![]() se determina cu
ajutorul:
se determina cu
ajutorul: ![]() , rezultand valorile:
, rezultand valorile:
![]() (1.4)
(1.4)
Ecuatia
(2) devine: 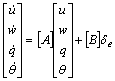 (1.5)
(1.5)
Matricea
iesirilor este: ![]() (1.6)
(1.6)
Trasarea raspunsurilor sistemului la
comenzi treapta si impuls Dirac se vor face pentru scurta perioada (starile ![]() si
si ![]() ), respectiv lunga
perioada (starile
), respectiv lunga
perioada (starile ![]() si
si ![]() ).
).
![]() sunt moduri rapide, dinamica lor detrmina scurta perioada
sunt moduri rapide, dinamica lor detrmina scurta perioada
![]() sunt moduri lente,
dinamica lor determina fugoida (lunga perioada)
sunt moduri lente,
dinamica lor determina fugoida (lunga perioada)
Scurta perioada se va decupla de dinamica longitudinala astfel:
![]() (1.7)
(1.7)
unde
![]() ,
(1.8)
,
(1.8)
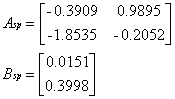 (1.9)
(1.9)
![]() ;
; ![]() (1.10)
(1.10)
1.1.1 Programul prezentat mai jos realizeaza trasarea
raspunsurilor sistemului la comenzi treapta ![]() si impuls Dirac
folosind comenzile step si impulse.
si impuls Dirac
folosind comenzile step si impulse.
% Trasarea raspunsurilor la comenzi treapta si impuls Dirac
clear;clc;
disp('Trasarea raspunsurilor sistemului in timp la comenzi treapta si impuls Dirac');disp(
disp('Vectorul de stare:');disp( );disp('x=[u alfa q teta]'''
A=[ -0.0083 -9.2618 0.1046 -9.8100;
0.0000 -1.8535 -0.2052 0;
%matricea de stabilitate
B=[-0.23325E+01; 0.15131E-01; 0.39984E+00; 0.00000E+00]; %matricea de comanda
disp('Matricea de stabilitate:');A
disp('Matricea de comanda:');B
%C=[Cu Ca Cq Cth] -matrici de iesire pt: viteza, alfa, q, theta
Cu=[1 0 0 0];
Ca=[0 1 0 0];
Cq=[0 0 1 0];
Cth=[0 0 0 1];
%tsp;tph=timpi de raspuns pentru scurta perioada respectiv fugoida;
tsp=0:0.01:5;
tph=0:1:2000;
%Sistemul nedecuplat
u=step(A,B,Cu,0,1,tph);
a=step(A,B,Ca,0,1,tph);
q=step(A,B,Cq,0,1,tph);
theta=step(A,B,Cth,0,1,tph);
%scurta perioada
disp('Matricea de stabilitate-scurta perioada:'
Asp=A(2:3,2:3)
disp('Matricea de comanda-scurta perioada:'
Bsp=B(2:3)
alfa=step(Asp,Bsp,[1 0],0,1,tsp);
q=step(Asp,Bsp,[0 1],0,1,tsp);
% Plotarea raspunsurilor la comenzi treapta unitate
%sistem nedecuplat
plot(tph,u,tph,theta*50,
title('bf Raspunsul sistemului la comanda treapta unitate-sistem nedecuplat'
xlabel('t[s]'
ylabel('u[m/s], theta*50 [rad]'
grid on
legend('u' 'theta'
figure;
plot(tsp,alfa,tsp,q,
title('bf Raspunsul sistemului la comanda treapta unitate-sistem nedecuplat'
xlabel('t[s]'
ylabel('alpha,q[rad/s]'
legend('alpha' 'q'
grid on
figure;
%pentru lunga perioada (fugoida);
plot(tph,u,tph,theta*50,
title('bf Raspunsul sistemului la comanda treapta unitate-fugoida'
xlabel('t[s]'
ylabel('u[m/s], theta*50 [rad]'
legend('u' 'theta'
grid on
figure;
%pentru scurta perioada;
plot(tsp,alfa,tsp,q,
title('bf Raspunsul sistemului la comanda treapta unitate-scurta perioada'
xlabel('t[s]'
ylabel('alpha,q[rad/s]'
legend('alpha' 'q'
grid on
figure;
% Plotarea raspunsului la impuls Dirac;
%sistem nedecuplat
system_u=ss(A,B,Cu,0);
system_theta=ss(A,B,Cth,0);
impulse(system_u,system_theta*50,
title('bf Raspunsul sistemului la impuls Dirac-sistem nedecuplat'
xlabel('t[s]'
ylabel('u[m/s],theta*50 [rad/s]'
legend('u' 'theta'
grid on
figure;
system_alfa=ss(A,B,Ca,0);
system_q=ss(A,B,Cq,0);
impulse(system_alfa,system_q,
title('bf Raspunsul sistemului la impuls dirac-sistem nedecuplat'
xlabel('t[s]'
ylabel('alpha,q[rad/s]'
legend('alpha' 'q'
grid on
figure;
%pentru fugoida;
system_u=ss(A,B,Cu,0);
system_theta=ss(A,B,Cth,0);
impulse(system_u,system_theta*50,
title('bf Raspunsul sistemului la impuls Dirac-fugoida'
xlabel('t[s]'
ylabel('u[m/s], theta*50 [rad]'
legend('u' 'theta'
grid on
figure;
%pentru scurta perioada;
system_alfa=ss(Asp,Bsp,[1 0],0);
system_q=ss(Asp,Bsp,[0 1],0);
impulse(system_alfa,system_q,
title('bf Raspunsul sistemului la impuls Dirac-scurta perioada'
xlabel('t[s]'
ylabel('alpha,q[rad/s]'
legend('alpha' 'q'
grid on
1.1.2 Rezultatul Programului
Trasarea raspunsurilor sistemului in timp la comenzi treapta si impuls Dirac
Vectorul de stare:
x=[u alfa q teta]'
Matricea de stabilitate:
A =
Matricea de comanda:
B =
Matricea de stabilitate-scurta perioada:
Asp =
Matricea de comanda-scurta perioada:
Bsp =
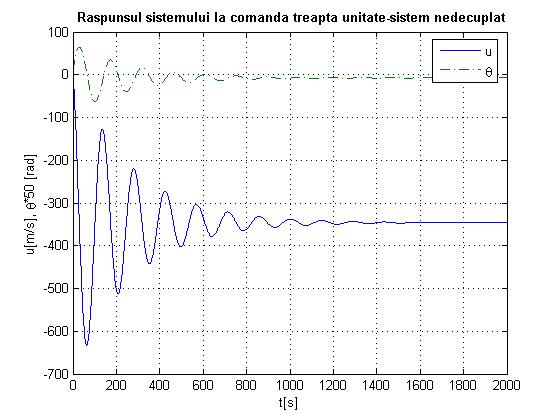
Fig.1.1
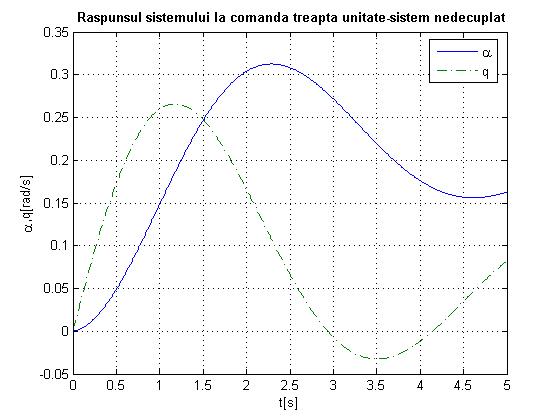
Fig.1.2
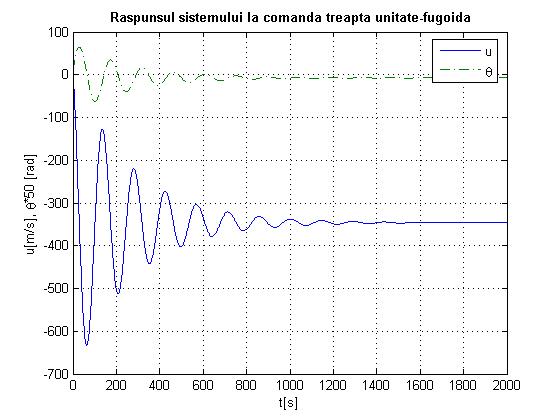
Fig.1.3
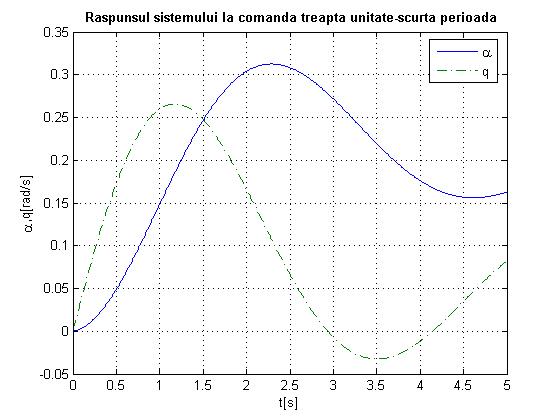
Fig.1.4
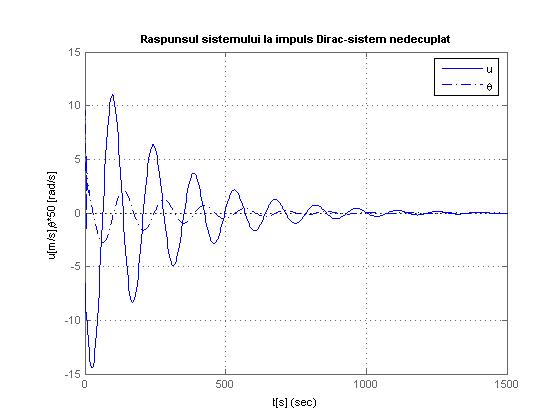
Fig.1.5
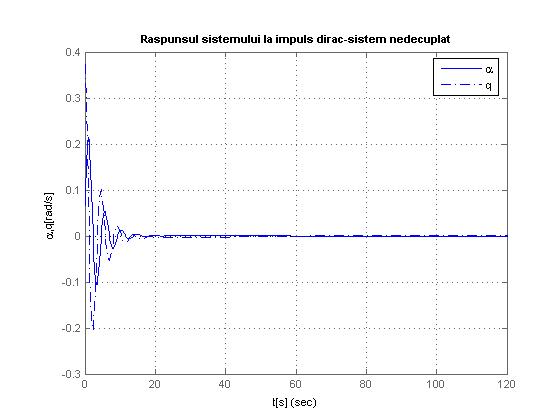
Fig.1.6
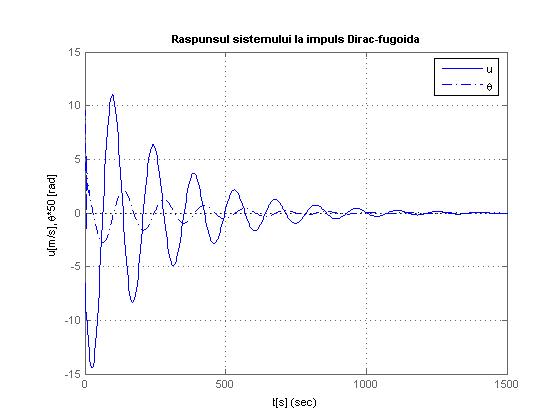
Fig.1.7
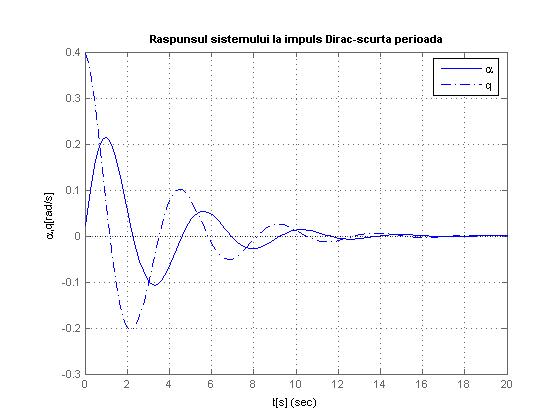
Fig.1.8
1.1.3 Observatii:
Din rezultatele programului, putem observa ca matricea de stabilitate Asp a scurtei perioade, asupra careia daca aplicam comanda eig(Asp) vom avea valorile proprii:
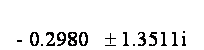
de unde ne rezulta ca matricea de stabilitate a scurtei perioade este stabila.
Din
fig.1.1, 1.3, 1.35 observa m o stabilizare rapida a unghiului de atitudine
logitudinala ![]() , si de un timp lung de relgare a vitezei u.
, si de un timp lung de relgare a vitezei u.
Deasemenea graficele 1.5, 1.6, 1.7, 1.8 raspunsurile la impuls Dirac, observam ca se stabilizeaza, asa cum era de asteptat, la 0.
1.2. Specificatii MIL - STD - 1797 privind calitatile de zbor
Clasificarea avioanelor:
-Avioane mici, usoare: utilitare, antrenament usor, avioane de observatie.
-Avioane de greutate medie, cu manevrabilitate de la slab la mediu: avioane grele, avioane de transport usor/mediu, avioane antisubmarine, avioane de recunoastere, avioane de bombardament tactic, avioane grele de atac, avioane de antrenament pentru clasa II.
-Avioane mari, grele, cu manevrabilitate de la mediu la usor: avioane de transport greu, bombardament greu, patrulare, avioane de antrenament clasa III.
-Avioane cu manevrabilitate ridicata: de vanatoare si interceptie, atac, de recunoastere tactica, antrenament clasa IV.
Categorii ale fazelor de zbor:
-Neterminale
A - acele faze de zbor care necesita manevre rapide, precizie in urmarire:
faze de lupta aeriana;
atac la sol;
lansare de armament;
recunoastere;
alimentarea in zbor;
cautare antisubmarin;
zbor in formatie stransa.
B - acele faze de zbor realizate prin manevre graduale fara precizie:
urcare croaziera;
coborare;
coborare de urgenta.
- Terminale - realizate cu control précis
decolarea;
apropierea;
aterizarea.
Nivele ale calitatilor de zbor:
cu claritate adecvata pentru fazele de zbor ale misiunii
pentru indeplinirea misiunii de zbor, dar cu un anumit efort de
la pilot sau cu degradarea eficacitatii indeplinirii misiunii
calitate de zbor astfel incat avionul poate fi controlat in
siguranta, dar efortul pilotului este excesiv, iar eficienta misiunii este neadecvata.
1.3. Proiectarea SAS pentru
scurta perioada. Criteriul C* si criteriul ![]()
Pentru a stabiliza scurta perioada conform principiului sistemului SAS, sistemului dinamic al avionului i se aplica o amplificare, in reactie pe una dintre iesiri. S-a ales sa se amplifice componenta care da viteza unghiulara de tangaj (q).
Scurta perioada este extrasa din sistemul dinamic original dupa cum urmeaza:
![]()
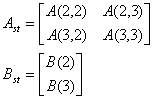 (1.11)
(1.11)
![]()
Pentru a verifica eficitatea aplicarii amplificarii se va determina raspunsul scurtei perioade la impuls si treapta.
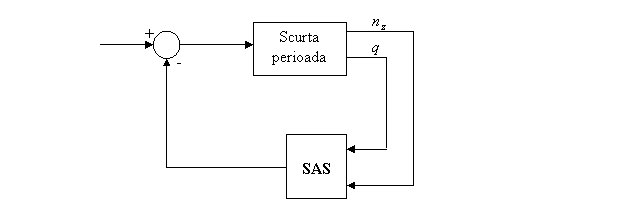
Fig. 1.9 SAS
Dinamica longitudinala a avionului este reprezentata de relatiile urmatoare:
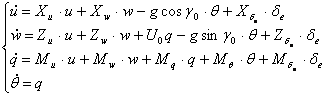 (1.12)
(1.12)
Scurta perioada este deschisa de ecuatiile:
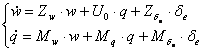 (1.13)
(1.13)
Impartim
prin ![]() prima ecuatie a sistemului
(1.13) si obtinem:
prima ecuatie a sistemului
(1.13) si obtinem:
![]() (1.14)
(1.14)
Daca
termenul care contine expresia ![]() se neglijeaza, atunci
se poate scrie:
se neglijeaza, atunci
se poate scrie:
![]() (1.15)
(1.15)
deoarece: ![]()
![]() (1.16)
(1.16)
Acceleratia normala se poate scrie:
![]() (1.17)
(1.17)
Din aceasta ecuatie se obtine:
![]() (1.18)
(1.18)
Se considera:
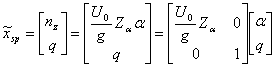 (1.19)
(1.19)
Se face schimbarea de stari:
![]() (1.20)
(1.20)
![]() (1.21)
(1.21)
Pentru scurta perioada se mai poate scrie:
![]() , (1.22)
, (1.22)
unde: ![]()
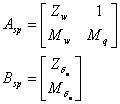 (1.23)
(1.23)
![]()
Polinomul caracteristic al matricei de stabilitate a scurtei perioade este:
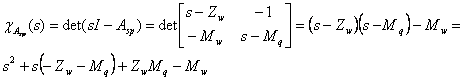 (1.24)
(1.24)
Iar daca se face notatia:
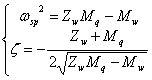 , (1.25)
, (1.25)
Relatia (1.24) se mai poate scrie:
![]() (1.26)
(1.26)
Specificatiile MIL-STD-1797 (figura 1.7) prevad ca pentru scurta perioada:
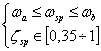 (1.27)
(1.27)
unde ![]() si
si ![]() se determina la
intersectia curbelor din figura 1.7 cu dreapta:
se determina la
intersectia curbelor din figura 1.7 cu dreapta:
![]()
![]()
![]() (1.28)
(1.28)
In ecuatia de mai sus ![]() este viteza avionului
si are o valoare cunoscuta,
este viteza avionului
si are o valoare cunoscuta, ![]() se citeste din grafic
iar
se citeste din grafic
iar ![]() se ia din matricea A.
se ia din matricea A.
Se determina:![]()
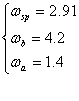 (1.29)
(1.29)
Deoarece viteza ascensionala nu se
poate masura cu o acuratete foarte mare la bordul avionului, facem schimbarea
de variabila ![]() unde
unde ![]() este acceleratia
verticala - folosind relatiile:
este acceleratia
verticala - folosind relatiile: ![]() (1.30)
(1.30)
![]() (1.31)
(1.31)
![]() (1.32)
(1.32)
![]() (1.33)
(1.33) 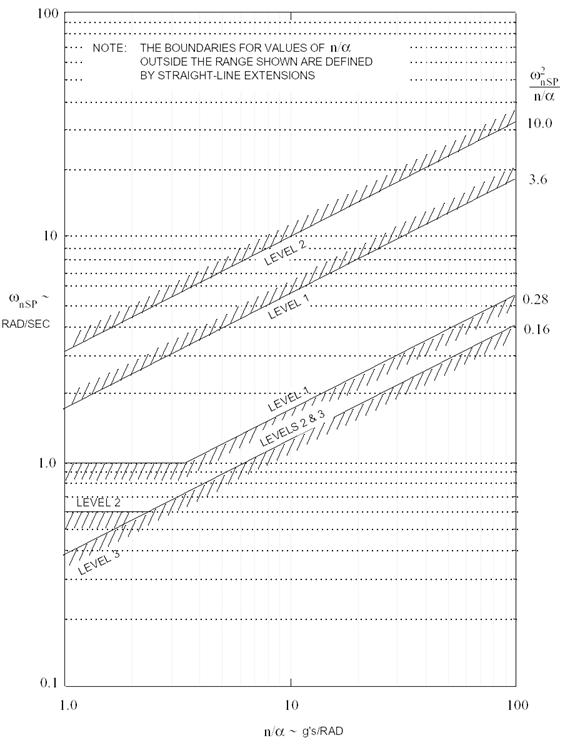
Fig. 1.10 Short Period Frequency rquirements - Category A Flight Phases
Din relatia (1.17) rezulta:
![]() (1.34)
(1.34) ![]() , (1.35)
, (1.35)
unde s-a tinut cont
de faptul ca ![]() .
.
Matricea de transformare a
vectorului de stare, ![]()
 (1.36)
(1.36)
este:
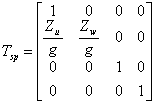 (1.37)
(1.37)
Matricea de transformare ![]() a vectorului de
stare
a vectorului de
stare  este:
este:
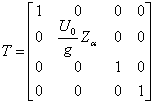 . (1.38)
. (1.38)
Dupa transformare, sistemul initial ![]() va deveni:
va deveni:
![]() , (1.39)
, (1.39)
iar vectorul de stare
![]() :
:
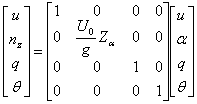 (1.40)
(1.40)
Din ecuatia:
![]() (1.41)
(1.41)
rezulta:
![]() (1.42)
(1.42)
![]()
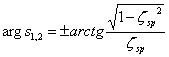 (1.43)
(1.43)
Alocarea polilor
Pentru ca un avion sa poata indeplini criteriile puse de MIL, polii scurtei perioade trebuie sa se afle intr-un domeniu bine stabilit conform specificatiilor MIL.
Programul de alocare a polilor realizeaza acest lucru dupa cum urmeaza:
se considera viteza avionului
in functie de viteza, se determina domeniul in care vor fi alocati polii scurtei perioade conform specificatiilor MIL
pentru acest domeniu se genereaza un patrulater in interiorul caruia se afla valorile unor amplificari care vor fi folosite pentru verificarea criteriului C*
Polii
scurtei perioade trebuie sa apartina unei coroane circulare care are drept raze
doua valori ce se determina din specificatiile MIL. Din punct de vedere
geometric acest fapt poate fi reprezentat: 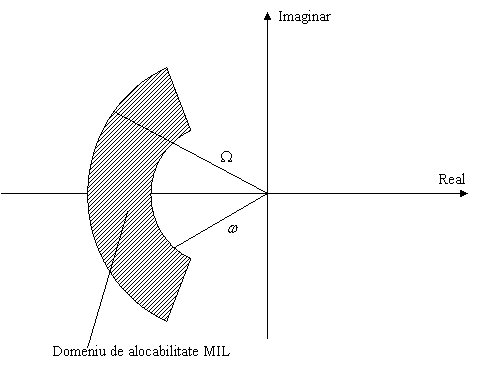
In figura 1.11 este reprezentata
dependenta solutiilor ecuatiei (1.42) in functie de ![]() si
si ![]() atunci cand acestea
variaza intre valorile permise de specificatiile MIL .
atunci cand acestea
variaza intre valorile permise de specificatiile MIL .
Observatie
ramura (1) - ![]() ;
;![]()
ramura (2) - ![]() ;
;![]()
ramura (3) - ![]() ;
;![]()
ramura (4) - ![]() ;
;![]()
Se rezolva problema de alocare:
![]() (1.44)
(1.44)
unde
![]() si se traseaza curba
si se traseaza curba ![]() . Orice punct
. Orice punct ![]() din domeniul delimitat
de aceasta curba are proprietatea:
din domeniul delimitat
de aceasta curba are proprietatea:
![]() (1.45)
(1.45)
Se alege unul din aceste puncte, de exemplu:
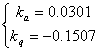 (1.46)
(1.46)
Criteriul C*
In continuare se va aplica criteriul C* pentru analiza SAS-ului. Criteriul C* ne permite determinarea comportarii scurtei perioade a dinamicii avionului. Daca un avion se afla intr-un domeniu care este considerat acceptabil de catre piloti, inseamna ca avionul raspunde conform cerintelor.
![]() (1.47)
(1.47)
unde :
![]() iar
iar ![]() si
si ![]() sunt raspunsurile scurtei perioade la comanda treapta
unitate.
sunt raspunsurile scurtei perioade la comanda treapta
unitate.
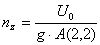 fiind acceleratia longitudinala
a avionului
fiind acceleratia longitudinala
a avionului
![]() Pentru a putea modifica curba determinata, astfel incat aceasta sa se
afle in domeniul criteriului C*,
dinamicii scurtei perioade i se aplica un element de intarziere de forma:
Pentru a putea modifica curba determinata, astfel incat aceasta sa se
afle in domeniul criteriului C*,
dinamicii scurtei perioade i se aplica un element de intarziere de forma:
unde ![]() este o variabila intre
2 si 5
este o variabila intre
2 si 5
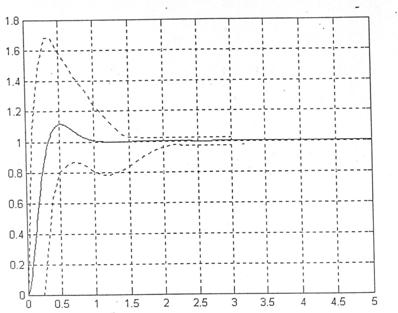
Fig. 1.12 Criteriul C*
Din figura se observa ca avionul (linia continua) se incadreaza in limitele dictate de criteriul C*(liniile punctate), ceea ce inseamna ca avionul are o comportare foarte buna in timpul zborului.
Criteriul ![]()
Criteriul
![]() este asemanator cu
criteriul C*, adica are acelasi rol de a determina comportarea dinamicii
scurtei perioade in timpul zborului. Diferenta este ca pentru acest criteriu
valoarea care este supravegheata este q
(viteza de tangaj).
este asemanator cu
criteriul C*, adica are acelasi rol de a determina comportarea dinamicii
scurtei perioade in timpul zborului. Diferenta este ca pentru acest criteriu
valoarea care este supravegheata este q
(viteza de tangaj).
Formula dupa care se formeaza curba Q este:
![]() , (1.49)
, (1.49)
unde:
![]() raspunsul la treapta
unitate
raspunsul la treapta
unitate
![]() valoarea stabilizata a
lui
valoarea stabilizata a
lui ![]()
Pentru
a avea o imagine cat mai buna asupra comportarii sistemului dinamic fata de
cele doua criterii, in criteriul ![]() elementul de
intarziere este mentinut acelasi ca la criteriul C*, astfel putandu-se observa
diferentele dintre cele doua criterii.
elementul de
intarziere este mentinut acelasi ca la criteriul C*, astfel putandu-se observa
diferentele dintre cele doua criterii.
Reprezentarea grafica a criteriului q/qst este redata in fig urmatoare
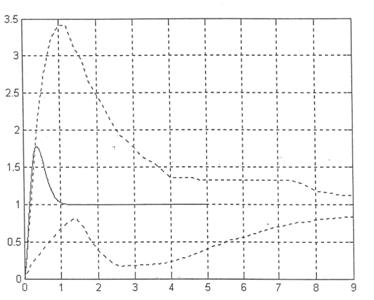
Fig. 1.13. Criteriul q/qst
Din
figura se poate observa ca folosind elementul de intarziere care este cel mai
potrivit pentru criteriul C*, curba generata de comportarea dinamicii avionului
pentru criteriul ![]() (linia continua) se
afla la linia de acceptabilitate.
(linia continua) se
afla la linia de acceptabilitate.
1.3.1. Programul pentru stabilizarea scurtei perioade
clear;clc;
disp('Stabilizarea scurtei perioade'
A= [-0.0083 -9.2618 0.1046 -9.8100 ;
%matrice de stabilitate
B=[
0.0151;
0.3998;
%matrice de comanda
Asp=A(2:3,2:3); Bsp=B(2:3); %pentru scurta perioada
ca=[1 0]; cq=[0 1]; %Matricea de iesiri pentru alfa si q (scurta perioada)
t=0:0.1:10 %Timp de stabilizare
var=0;
for kq=-1:0.1:1
A_sp=Asp-Bsp*[kq 0];
Vsp=eig(A_sp);
if real(Vsp(1))<0 & real(Vsp(2))<0 & imag(Vsp(1))~=0 & real(Vsp(1))>3 & real(Vsp(2))>-3 & abs(imag(Vsp(1)))>4
spkq=kq;
var=1;
break
end
if var==1
break
end
end
disp('Valorile proprii'
disp(eig(Asp));
disp('Valoarea amplificarii'
disp('kq='
disp(kq);
%Plotarea raspunsurilor la comanda treapta unitate:
alfa=step(Asp,Bsp,[1 0],0,1,t);
q=step(Asp,Bsp,[0 1],0,1,t);
plot(t,alfa);
title('bf Raspunsul sistemului la comanda treapta unitate-alfa'
xlabel('timp[s]'); ylabel('alpha'
grid on
figure;
plot(t,q);
title('bf Raspunsul sistemului la comanda treapta unitate-q'
xlabel('timp[s]'); ylabel('q[rad/s]'
grid on
figure;
%%Plotarea raspunsurilor la impuls Dirac;
alfa_imp=impulse(Asp,Bsp,[1 0],0,1,t);
q_i=impulse(Asp,Bsp,[0 1],0,1,t);
plot(t,alfa_imp);
title('bf Raspunsul sistemului la impuls Dirac-alfa'
xlabel('timp[s]'); ylabel('alpha_i'
grid on
figure;
plot(t,q_i);
title('bf Raspunsul sistemului la impuls Dirac-q'
xlabel('timp[s]'
ylabel('q_i[rad/s]'
grid on
1.3.2. Rezultatul programului pentru stabilizarea scurtei perioade
Stabilizarea scurtei perioade
t =
Columns 1 through 10
Columns 11 through 20
Columns 21 through 30
Columns 31 through 40
Columns 41 through 50
Columns 51 through 60
Columns 61 through 70
Columns 71 through 80
Columns 81 through 90
Columns 91 through 100
Column 101
Valorile proprii
-0.2980 + 1.3511i
-0.2980 - 1.3511i
Valoarea amplificarii
kq=1
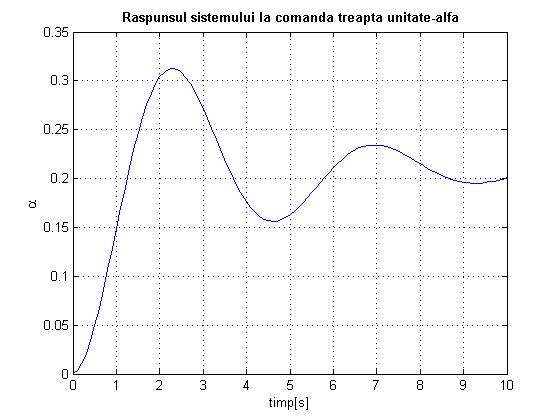
Fig.1.14
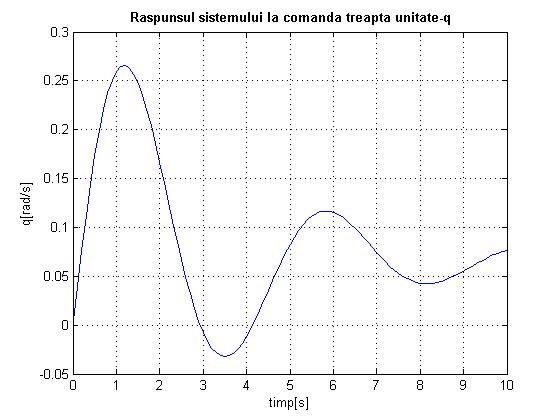
Fig.1.15
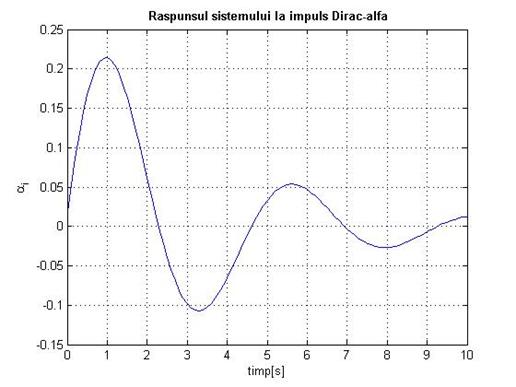
Fig.1.16
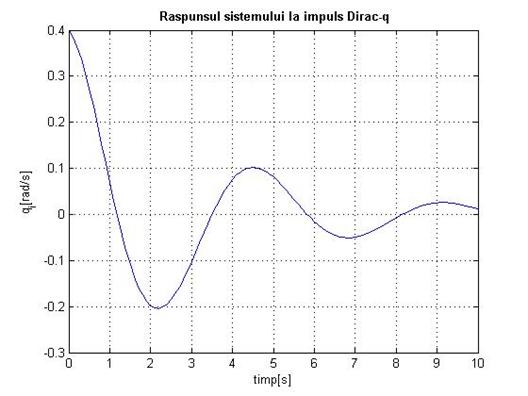
Fig.1.17
1.3.3 Programul pentru alocarea polilor
%Alocarea polilor
clear;
clc;
disp('Alocarea polilor'
disp(
A= [-0.0083 -9.2618 0.1046 -9.8100 ;
0 -1.8535 -0.2052 0 ;
0 0 1.0000 0 ]; %matrice de stabilitate
B=[-2.3325;
0.0151;
0.3998;
%matrice de comanda
%Valorile omega_a si omega_b (nz/alpha)
omega_a=1.4;
omega_b=4.2;
g=9.81; %acceleratia gravitationala [m/s^2]
j=sqrt(-1);
T=eye(4); %matricea de transformare T
T(2,1)=A(2,1)/g %(A,b,c) ~ (TAT^(-1),Tb,cT^(-1)
%Se face schimbarea de stare folosind matricea T
A=T*A*inv(T);
B=T*B;
%C=C*inv(T)
save matrici A B
%Determinarea scurtei perioade
Asp=A(2:3,2:3);
Bsp=B(2:3);
save matrici_sp Asp Bsp
%ramura 1
omega=omega_a;
k=0;
for zeta=0.35:0.01:1
k=k+1;
s1(k)=-zeta*omega+j*omega*sqrt(1-zeta^2);
s2(k)=-zeta*omega-j*omega*sqrt(1-zeta^2);
%Lamda (Asp-Bsp [kalfa kq]) =
k_poli=acker(Asp,Bsp,[s1(k) s2(k)]);
kalfa=k_poli(1);
kq=k_poli(2);
k1(k,1)=kalfa;
k1(k,2)=kq;
end
plot(s1);
hold on
plot(s2);
hold on
clear s1 s2
%ramura 2
omega=omega_b
k=0;
for zeta=0.35:0.01:1
k=k+1;
s1(k)=-zeta*omega+j*omega*sqrt(1-zeta^2);
s2(k)=-zeta*omega-j*omega*sqrt(1-zeta^2);
%Lamda (Asp-Bsp [kalfa kq]) =
k_poli=acker(Asp,Bsp,[s1(k) s2(k)]);
kalfa=k_poli(1);
kq=k_poli(2);
k2(k,1)=kalfa;
k2(k,2)=kq;
end
plot(s1);
hold on
plot(s2);
hold on
clear s1 s2
%ramura 3
zeta=0.35;
k=0;
for omega=omega_a :0.1:omega_b
k=k+1;
s1(k)=-zeta*omega+j*omega*sqrt(1-zeta^2);
s2(k)=-zeta*omega-j*omega*sqrt(1-zeta^2);
k_poli=acker(Asp,Bsp,[s1(k) s2(k)]);
kalfa=k_poli(1);
kq=k_poli(2);
k3(k,1)=kalfa;
k3(k,2)=kq;
end
plot(s1);
hold on
plot(s2);
axis([-15 15 -15 15]);
title('bf Proiectarea SAS-ului'
xlabel('Re s'
ylabel('Im s'
grid on
hold off
clear s1 s2
%ramura 4
zeta=1;
k=0;
for omega=omega_a :0.1:omega_b
k=k+1;
s1(k)=-zeta*omega+j*omega*sqrt(1-zeta^2);
s2(k)=-zeta*omega-j*omega*sqrt(1-zeta^2);
k_poli=acker(Asp,Bsp,[s1(k) s2(k)]);
kalfa=k_poli(1);
kq=k_poli(2);
k4(k,1)=kalfa;
k4(k,2)=kq;
end
%plotarea graficului kalfa=kalfa(kq)
figure;
plot(k1(:,2),k1(:,1),'b',k2(:,2),k2(:,1),'b',k3(:,2),k3(:,1),'b',k4(:,2),k4(:,1),'b'
title('bf Alocarea polilor'
xlabel('kq'
ylabel('kalfa'
grid on
%Analiza C*(t)
clear;
load cstar
load matrici_sp %incarca Asp si Bsp pentru scurta perioada;
t=0:0.01:3
disp('Alege un punct (kq, kalfa) din interiorul domeniului'
[kq,kalfa]=ginput(1);
disp('kq='
disp(kq);
disp('kalfa='
disp(kalfa);
nz=step((Asp-Bsp*[kalfa kq]),Bsp,[1 0],0,1,t);
q=step((Asp-Bsp*[kalfa kq]),Bsp,[0 1],0,1,t);
cstar=(nz-12.43*q)/(nz(length(t))-12.43*q(length(t)));
%trasarea graficului C*
figure;
plot(xcl,cl, ,xcu,cu, ,t,cstar);
%axis([0 3 0 2]);
title('bf Analiza C*(t)'
xlabel('t[s]'
ylabel('C*'
grid on
%varianta cu prefiltru
disp('Varianta cu prefiltru'
c=4
clear nz q cstar;figure;
[Ap,Bp,Cp,Dp]=tf2ss(1,[1 c]);
[Aspr, Bspr, Cspr, Dspr]=series(Ap, Bp, Cp,Dp, Asp-Bsp*[kalfa kq], Bsp, eye(2), zeros(2,1));
nz=step(Aspr, Bspr, Cspr(1,:),Dspr(1,:),1,t);
q=step(Aspr, Bspr, Cspr(2,:),Dspr(2,:),1,t);
cstar=(nz-12.43*q)/(nz(length(t))-12.43*q(length(t)));
%trasarea graficului C*
plot(xcl,cl, ,xcu,cu, ,t,cstar);
title('bf Analiza C*(t)(varianta cu prefiltru)'
xlabel('t[s]'
ylabel('C*'
grid on;figure;
%Criteriul q/qst
load qdiag
plot(xqu,qu, ,xql,ql, ,t,q/q(length(t)));
title('bf Analiza q/qst'
xlabel('t[s]'
ylabel('q/qst'
grid on
knz=kalfa;
save sas knz kq kalfa c
1.3.4 Rezultatul programului pentru alocarea polilor
Alocarea polilor
T =
omega =
t =
Columns 1 through 14
Columns 15 through 28
Columns 29 through 42
Columns 43 through 56
Columns 57 through 70
Columns 71 through 84
Columns 85 through 98
Columns 99 through 112
Columns 113 through 126
Columns 127 through 140
Columns 141 through 154
Columns 155 through 168
Columns 169 through 182
Columns 183 through 196
Columns 197 through 210
Columns 211 through 224
Columns 225 through 238
Columns 239 through 252
Columns 253 through 266
Columns 267 through 280
Columns 281 through 294
Columns 295 through 301
Alege un punct (kq, kalfa) din interiorul domeniului
kq= 10.0230
kalfa= 19.9342
Varianta cu prefiltru
c = 4
knz=kalfa
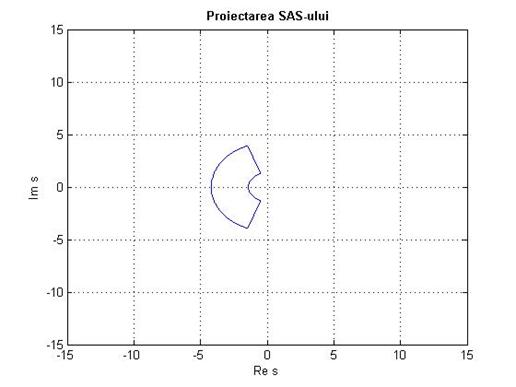
Fig.1.18
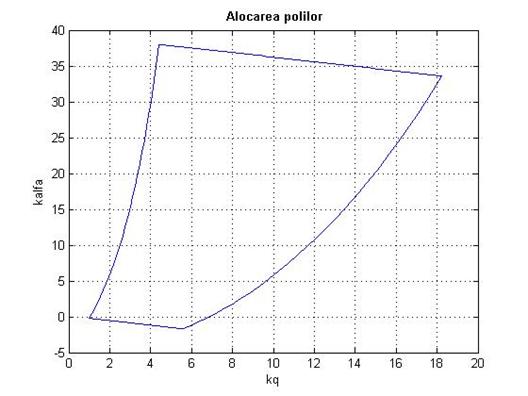
Fig.1.19
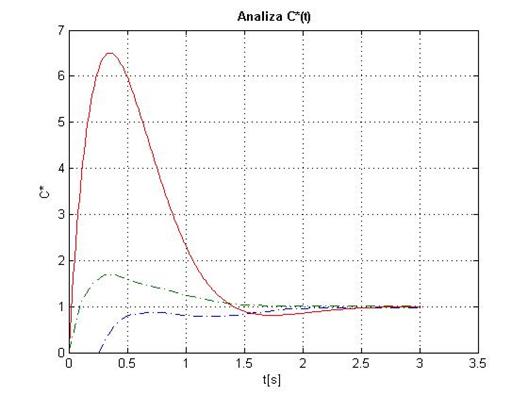
Fig1.20
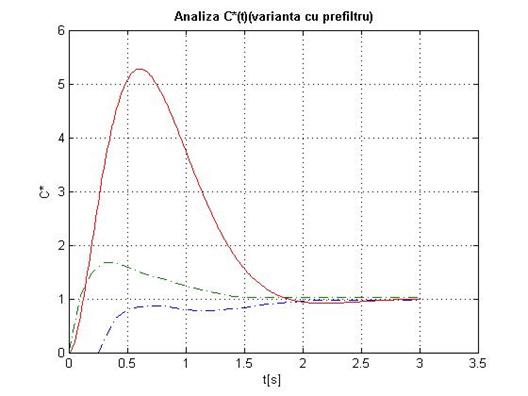
Fig.1.21
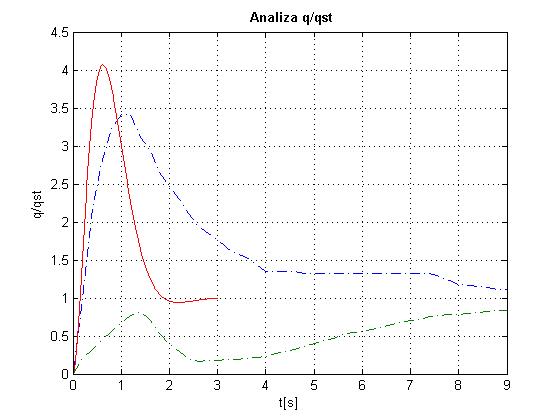
Fig.1.22
1.3.5 Observatii:
La analiza C* fara filtru, figura 1.20 putem observa cum avionul (linia continua) iese din limitele criteriului C*, astfel nu putem spune ca avionul are un comportament bun in timpul zborului. Daca privim analiza C* cu filtru, observam o imbunatatire a comportamentului aeronavei, aceasta mentinandu-se in limitele criteriului C*.
Este deasemnea de consemnat faptul ca altitudinea de calcul este 1000m, iar viteza de 150 m/s, o viteza mare pentru aceasta altitudinea pentru acest tip de aeronava.
1.4. Stabilizarea modurilor lente
Dupa determinarea completa a scurtei perioade, aici incluzand si verificarea celor doua criterii de calitate, se trece la determinarea fugoidei care la randul ei va fi stabilizata prin amplificare.
Pentru a obtine ecuatiile modurilor lente ale dinamicii longitudinale(fugoida), membrul drept al ecuatiilor corespunzatoare scurtei perioade se anuleaza, ceea ce inseamna ca in ecuatiile (1.12) impunem conditia :
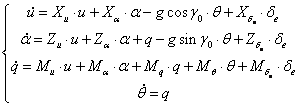 (1.12)
(1.12)
![]() (1.49)
(1.49)
Rezulta sistemul:
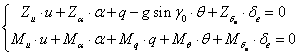 (1.50)
(1.50)
care
se rezolva in raport cu variabilele ![]() si
si ![]() .
.
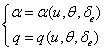 (1.51)
(1.51)
Relatiile (1.38) se introduc in celelalte doua ecuatii ale dinamicii longitudinale:
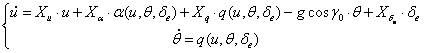 (1.52)
(1.52)
rezultand ecutiile fugoidei care se mai pot scrie:
![]() (1.53)
(1.53)
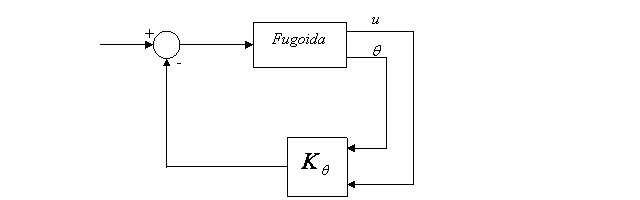
Fig. 1.22 - Fugoida
Valorile proprii ale fugoidei trebuie sa fie foarte apropiate de valorile proprii din dinamica longitudinala totala (fugoida + scurta perioada).
Pentru a stabiliza comportarea fugoidei
se vor aplica amplificarile ![]() si
si ![]() astfel:
astfel:
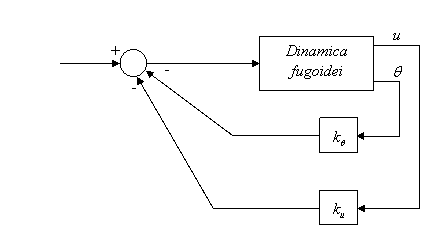
Fig. 1.23 - Sabilizarea fugoidei
Se poate aplica numai o singura
amplificare pe ![]() , dar pentru determinarea unei fugoide stabile se va aplica o
amplificare si pe
, dar pentru determinarea unei fugoide stabile se va aplica o
amplificare si pe ![]() .
.
Dupa determinarea amplificarilor si a valorilor proprii se poate spune ca fugoida a fost stabilizata ceea ce ne poate permite sa determinam raspunsul stabilizat al fugoidei.
Pentru aceasta se considera:
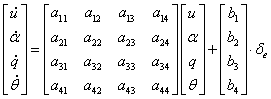 (1.54)
(1.54)
Conditia necesara este:
![]() (1.55)
(1.55)
Care se transcrie astfel:
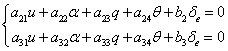 (1.56)
(1.56)
Se stie ca:
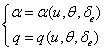 (1.57)
(1.57)
Relatiile se transcriu astfel:
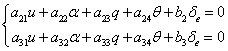 (1.58)
(1.58)
Se poate scrie:
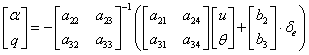 (1.59)
(1.59)
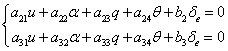 (1.60)
(1.60)
Altfel scris:
 (1.61)
(1.61)
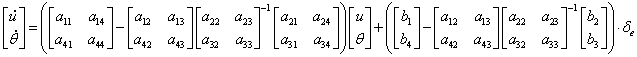
Identificam astfel matricea de stabilitate si matricea de comanda:
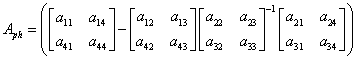 (1.63)
(1.63)
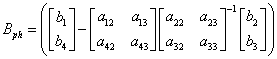 (1.63)
(1.63)
In general se poate scrie relatia:
![]() (1.64)
(1.64)
In concluzie, pentru a determina fugoida se folosesc matricea de stabilitate si matricea de comanda a dinamicii longitudinale a avionului astfel:
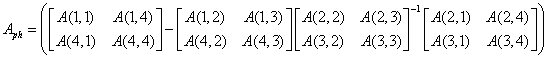
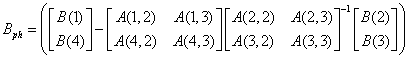 (1.66)
(1.66)
Dupa prelucrarea numerica a matricilor se obtin matricile de stabilitate si de comanda ale dinamicii fugoidei stabilizate.
Specificatiile MIL pentru modurile lente prevad ca pentru
nivelul 1 - ![]()
nivelul 2 - ![]()
nivelul 3 - ![]()
Se cauta ![]() astfel incat
astfel incat ![]() .
.
Determinarea sistemului SAS
Aplicarea sistemului SAS la dinamica longitudinala a unui avion va duce la o imbunatatire a stabilitatii acestuia, dar nu neaparat la imbunatatirea calitatii zborului. Sistemul SAS are menirea de a mentine stabil sistemul dinamic al avionului atunci cand acesta este supus unor mici variatii ale diferitilor parametri ai sai.
Sistemul SAS are ca metoda de aplicare generarea unor amplificari pe anumite iesiri ale sistemului dinamic nestabilizat al avionului si apoi trimiterea acestor amplificari pe intrarile sistemului dinamic, deci este vorba de amplificare in reactie.
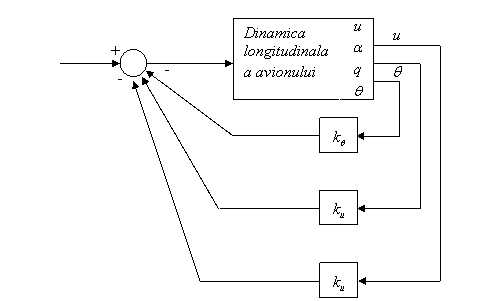
Fig. 1.24 Schema de principiu a SAS
Valorile amplificarilor care trebuie aplicate sunt cele determinate pentru stabilizarea scurtei perioade si respectiv a fugoidei. Matricea de stabilitate longitudinala va fi modificata astfel:
![]() (1.67)
(1.67)
Se observa ca matricea s-a schimbat semnificativ fata de matricea initiala, iar valorile proprii ale matricei sunt apropiate de valorile proprii ale matricelor de stabilitate dictate de MIL.
Pentru sistemul dinamic al avionului cuplat cu sistemul SAS se pot determina raspunsurile sistemului la treapta si impuls.
1.4.1 Programul pentru stabilirea fugoidei
clear;clc;
A=[ -0.0083 -9.2618 0.1046 -9.8100;
0 -1.8535 -0.2052 0;
0 0 1.0000 0]; %matricea de stabilitate
B=[-0.23325E+01; 0.15131E-01; 0.39984E+00; 0.00000E+00]; %matricea de comanda
Aph=[A(1,1) A(1,4); A(4,1) A(4,4)]-[A(1,2) A(1,3);A(4,2) A(4,3)]*inv([A(2,2) A(2,3); A(3,2) A(3,3)])*[A(2,1) A(2,4); A(3,1) A(3,4)];
Bph=[B(1); B(4)]-[A(1,2) A(1,3);A(4,2) A(4,3)]*inv([A(2,2) A(2,3); A(3,2) A(3,3)])*[B(2); B(3)];
Cph=[1 1];
Dph=zeros(1,2);
disp('Aph'
disp(Aph);
disp('Bph'
disp(Bph);
vp1=eig(Aph);
disp('vp1'
disp(vp1);
t=0:0.1:7;
var=0;
for kteta=0:0.1:1
for ku=-2:0.1:2
Ast=Aph-Bph*[ku kteta];
vp=eig(Ast);
if real(vp(1))<-0.01 & real(vp(2))<-0.01 & abs(imag(vp(1)))==abs(imag(vp(2)))
disp('Asp');disp(Ast);
disp('ku');disp(ku);
disp('kteta');disp(kteta);
disp('vp(1)');disp(vp(1));
disp('vp(2)');disp(vp(2));
var=1;
break
end
end
if var==1
break
end
end
u=step(Ast,Bph,[1 0],Dph,1,t);
plot(t,u);
title('Raspunsul sistemului la comanda treapta unitate-u'
xlabel('t[s]'
ylabel('u[m/s]'
grid on
figure;
theta=step(Ast,Bph,[0 1],Dph,1,t);
plot(t,theta);
title('Raspunsul sistemului la comanda treapta unitate- theta'
xlabel('t[s]'
ylabel('theta[rad]'
grid on
figure;
u_i=impulse(Ast,Bph,[1 0], Dph,1,t);
plot(t,u_i);
title('Raspunsul sistemului la impuls Dirac-u'
xlabel('t[s]'
ylabel('u_i[m/s]'
grid on
figure;
theta_i=impulse(Ast,Bph,[0 1],Dph,1,t);
plot(t,theta_i);
title('Raspunsul sistemului la impuls Dirac- theta'
xlabel('t[s]'
ylabel('theta _i[rad]'
grid on
1.4.2 Rezultatul programului pentru stabilirea fugoidei
Aph
Bph
vp1
-0.0040 + 0.0434i
-0.0040 - 0.0434i
Asp
ku
kteta
vp(1)
vp(2)
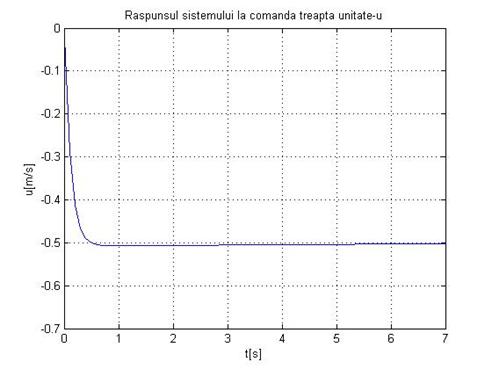
Fig.1.25 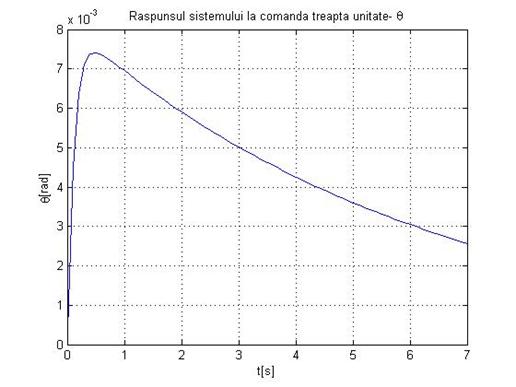
Fig.1.26
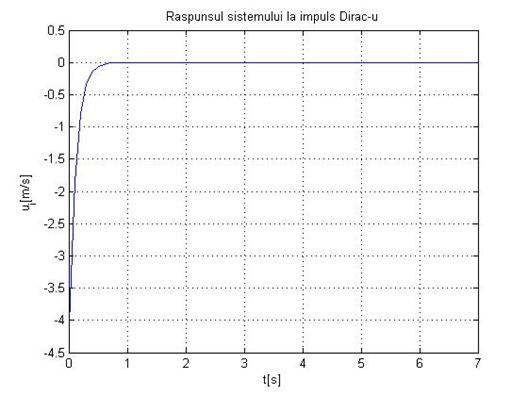
Fig.1.27
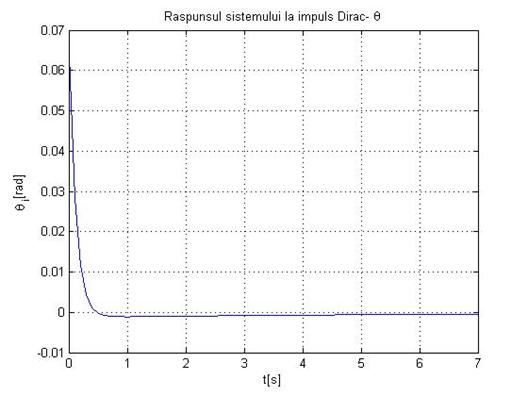
Fig.1.28
1.4.3 Program de proiectare pentru SAS
clear;clc;
A=[ -0.0083 -9.2618 0.1046 -9.8100;
0.0001 -1.8535 -0.2052 0;
%matricea de stabilitate
B=[-0.23325E+01 0.15131E-01 0.39984E+00 0.00000E+00 %matricea de comanda
C=eye(4);
D=zeros(4,1);
kq=
ku=-2;
ktheta=0;
Asas=A-B*[0,ku*(150/9.81)*A(2,2),kq,ktheta];
clc;
vp1=eig(A);
vp2=eig(Asas);
disp('Valorile proprii ale matricei A'
disp('vp1'
disp(vp1);
disp('Valorile proprii ale matricei Asas'
disp('vp2'
disp(vp2);
disp('Matricea de stabilitate Asas:'
disp('Asas'
disp(Asas);
figure;
impulse(Asas,B,C,D);
figure;
step(Asas,B,C,D);
1.4.4 Rezultatul programului pentru SAS
Valorile proprii ale matricei A
vp1
-0.2980 + 1.3496i
-0.2980 - 1.3496i
-0.0042 + 0.0457i
-0.0042 - 0.0457i
Valorile proprii ale matricei Asas
vp2
-2.3939 + 1.5002i
-2.3939 - 1.5002i
-0.0025 + 0.0412i
-0.0025 - 0.0412i
Matricea de stabilitate Asas:
Asas
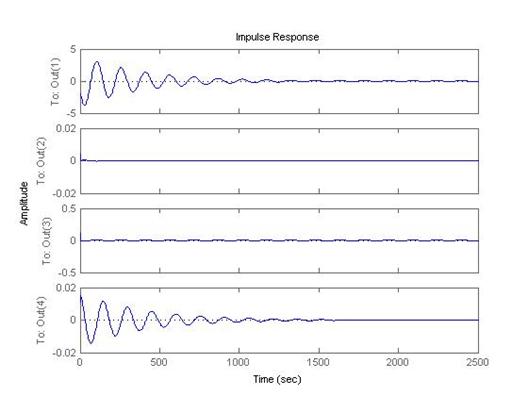
Fig.1.29
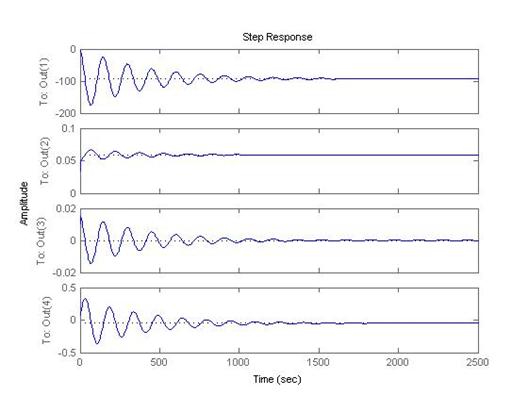
Fig.1.30
Sistemul rezultant (Ar, Br, Cr, Dr) este prezentat in figura 2.1.
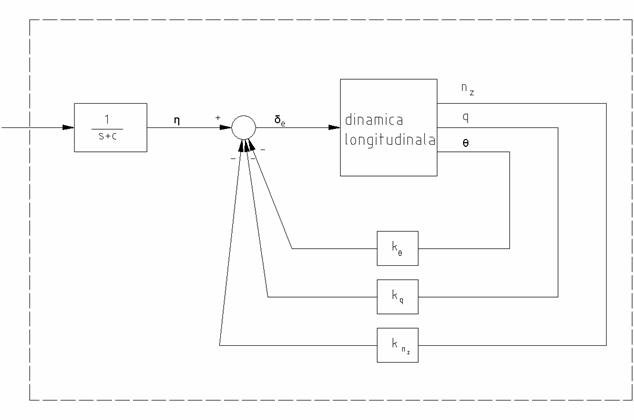
Fig. 2.1 - Sistemul rezultant
Daca explicitam comanda ![]() in functie de
in functie de ![]() atunci rezulta:
atunci rezulta:
![]() (2.1)
(2.1)
unde
 (2.2)
(2.2)
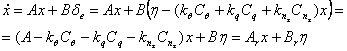 (2.3)
(2.3)
Am notat
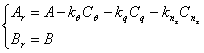 (2.4)
(2.4)
Se verifica daca ![]() , unde
, unde ![]() sunt valorile proprii ale matricei
sunt valorile proprii ale matricei ![]()
Etapa I - Determinarea constantelor K si K0 in cazul in care toate starile sunt masurabile
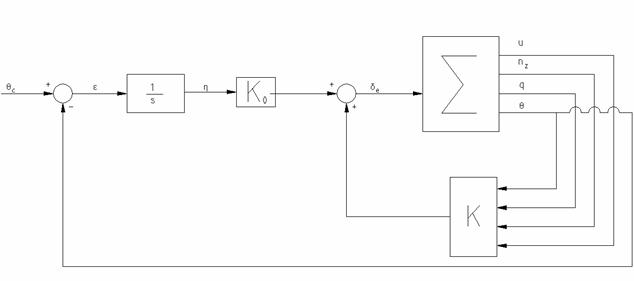
Fig. 2.2 - Pilotul automat pentru unghiul de atitudine longitudinala
Sistemul ![]() este
este
![]() . (2.5)
. (2.5)
Efectul elementului integrator este
![]() , (2.6)
, (2.6)
iar comanda ![]() se poate scrie
se poate scrie
![]() . (2.7)
. (2.7)
Rezulta sistemul:
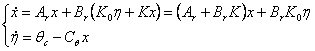 , (2.8)
, (2.8)
echivalent cu
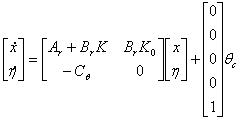 . (2.9)
. (2.9)
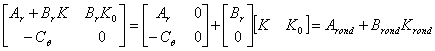 . (2.10)
. (2.10)
Am facut notatiile:
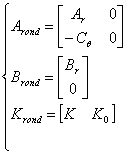 . (2.11)
. (2.11)
Daca se considera
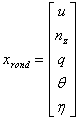 , (2.12)
, (2.12)
atunci relatia (5.9) devine
 . (2.13)
. (2.13)
Constantele ![]() si
si ![]() se calculeaza tratand
problema ca una liniar-patratica cu indicele de performanta
se calculeaza tratand
problema ca una liniar-patratica cu indicele de performanta
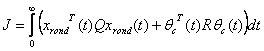 (2.14)
(2.14)
unde ponderile ![]() si
si ![]() se aleg ca fiind
se aleg ca fiind
 (2.15)
(2.15)
Se traseaza raspunsul sistemului la comanda treapta unitate si impuls Dirac si se verifica daca valorile proprii ale matricei de stabilitate satisfac relatia
![]() (2.16)
(2.16)
Etapa II - Calculul filtrului Kalman
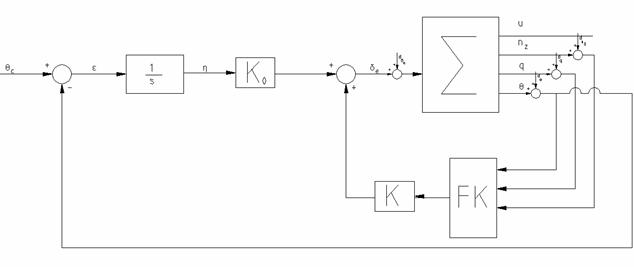
Fig. 2.5 - Pilotul automat pentru unghiul de atitudine longitudinala
In cazul in care nu toate starile sunt masurabile se va folosi un filtru Kalman
 (2.18)
(2.18)
unde

Se pot scrie relatiile:
 (2.20)
(2.20)
Se considera:
 (2.21)
(2.21)
Relatiile se pot scrie astfel:
 (2.22)
(2.22)
S-au considerat zgomotele asupra iesirilor:
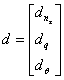 (2.23)
(2.23)
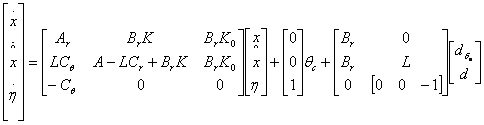 (2.24)
(2.24)
Se identifica:
 (2.25)
(2.25)
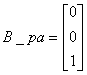 (2.26)
(2.26)
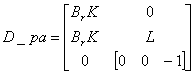 (2.27)
(2.27)
Consideram:
![]() (2.28)
(2.28)
![]() (2.29)
(2.29)
Calculam filtrul Kalman, verificand:
![]() (2.30)
(2.30)
Se testeaza pilotul automat in diferite conditii de turbulenta atmosferica:
a. simulare fara zgomote;
b. simulare cu zgomote asupra iesirilor;
c. simulare cu zgomote atat asupra iesirilor cat si a comenzii.
Metodele clasice de proiectare a reactiilor dupa stare(feedback) au pus la dispozitie proiectantilor, timp de multi ani, metodologii robuste de proiectare, dar care nu au fost extinse bine si in cazul sistemelor multivariabile.
Tehnicile moderne de proiectare
prezinta solutii si in cazul proiectarii compensatoarelor robuste
multivariabile. Teoria ![]() a fost dezvoltata de
la inceputurile anilor '80. Metoda se bazeaza pe minimizarea dupa frecventa a
valorilor maxime a unor functii de transfer alese de catre proiectant astfel
incat sa reprezinte obiectivele de proiectare. O calitate importanta a metodei
este aceea ca permite obtinerea stabilitatii si robustetei sistemului in
prezenta erorilor de modelare, a incertitudinilor si perturbatiilor (provenite
de la disturbatii sau zgomote). Semnalelor de intrare si de iesire li se pot
atasa ponderi dependente de frecventa (ponderi dinamice) pentru a se obtine un
sistem mai robust sau pentru a implini cerintele de proiectare.
a fost dezvoltata de
la inceputurile anilor '80. Metoda se bazeaza pe minimizarea dupa frecventa a
valorilor maxime a unor functii de transfer alese de catre proiectant astfel
incat sa reprezinte obiectivele de proiectare. O calitate importanta a metodei
este aceea ca permite obtinerea stabilitatii si robustetei sistemului in
prezenta erorilor de modelare, a incertitudinilor si perturbatiilor (provenite
de la disturbatii sau zgomote). Semnalelor de intrare si de iesire li se pot
atasa ponderi dependente de frecventa (ponderi dinamice) pentru a se obtine un
sistem mai robust sau pentru a implini cerintele de proiectare.
Un sistem este considerat a fi robust stabil daca, in orice stare (din domeniul prestabilit) s-ar afla, pentru orice incertitudine definita in jurul conditiilor nominale si in domeniul prestabilit, compensatorul este capabil sa il stabilizeze. Acelasi sistem detine performante robuste daca, in aceleasi conditii, compensatorul este capabil sa garanteze sistemului real performantele cerute.
![]() este un membru al
familiei de spatii numite Hardy, introduse de matematicianul Hardy. Este un
spatiu de functii in planul complex, care sunt analitice si marginite in
semiplanul drept. Importanta teoriei
este un membru al
familiei de spatii numite Hardy, introduse de matematicianul Hardy. Este un
spatiu de functii in planul complex, care sunt analitice si marginite in
semiplanul drept. Importanta teoriei ![]() in stabilitatea
robusta a fost prezentata de Glover in 1986.
in stabilitatea
robusta a fost prezentata de Glover in 1986.
Metodele de proiectare ![]() functioneaza prin minimizarea unei norme
functioneaza prin minimizarea unei norme ![]() a unei functii de
transfer in bucla inchisa astfel aleasa
incat sa reflecte stabilitatea si performanta robusta a sistemului. Norma poate
fi privita ca o masura a performantei unui sistem in functie de marimea semnalelor,
functiilor de transfer si a incertitudinilor.
a unei functii de
transfer in bucla inchisa astfel aleasa
incat sa reflecte stabilitatea si performanta robusta a sistemului. Norma poate
fi privita ca o masura a performantei unui sistem in functie de marimea semnalelor,
functiilor de transfer si a incertitudinilor.
Forma generala a sistemului generalizat T cu doua intrari si doua iesiri:
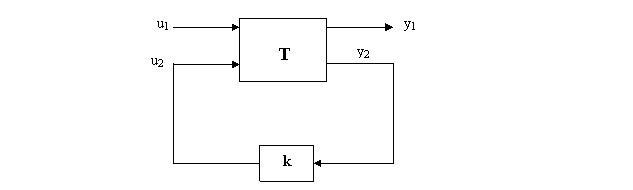
Fig.2.6
Intrarile si iesirile au urmatoarele semnificatii:
![]() este intrarea omogene
de tip zgo,ot alb
este intrarea omogene
de tip zgo,ot alb
![]() reprezinta variabila
de comanda
reprezinta variabila
de comanda
![]() este iesirea de
calitate
este iesirea de
calitate
![]() este iesirea masurata
este iesirea masurata
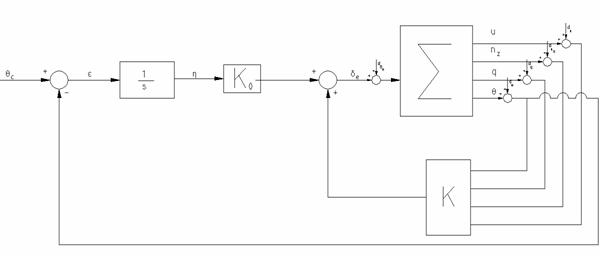
Fig. 2.7 - Pilotul automat pentru unghiul de atitudine longitudinala
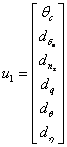
![]() (2.31)
(2.31)
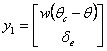
 (2.32)
(2.32)
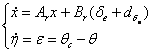 (2.33)
(2.33)
Relatia (2.32) se mai poate scrie
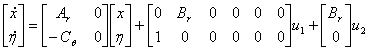 (2.34)
(2.34)
sau
![]() (2.35)
(2.35)
s-au facut notatiile
![]()
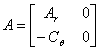
![]()
![]() (2.36)
(2.36)
![]() (2.37)
(2.37)
Notam :
![]()
![]()
![]() (2.38)
(2.38)
Atunci :
![]() (2.39)
(2.39)
 (2.40)
(2.40)
Notam :
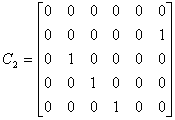
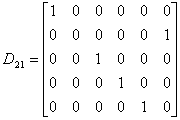
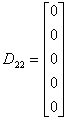
Atunci :
![]() (2.42)
(2.42)
2.3 Programul proiectare a pilotului automat pentru unghiul de atitudine longitudinala
clear;clc;
disp('Proiectarea pilotului automat pentru unghiul de atitudine longitudinala'
disp(
%Starile u,nz,q,theta se incarca din fisierul 'matrici.mat'
load matrici
%Valorile coeficientilor knz,kq,ktheta
load sas
knz=
kq=
ktheta=0;
c=4;
Asas=A-B*[0 knz kq ktheta];
Bsas=B;
Csas=[0 1 0 0; 0 0 1 0; 0 0 0 1];
Dsas=[0; 0; 0];
Af=-c;
Bf=1;
Cf=1;
Df=0;
[Ar, Br, Cr, Dr]=series(Af, Bf, Cf, Df, Asas, Bsas, Csas, Dsas);
plot(step(Ar,Br,[0 0 0 1 0], 0));
title('bf Raspunsul la comanda treapta unitate al avionului cu SAS-ul cuplat'
grid on
%Verificare Re(Lambda(Ar))<0
disp('Partea reala a valorilor proprii ale lui Ar'
disp(real(eig(Ar)));
%Metoda conventionala
disp('Metoda conventionala'
disp(
%Etapa I
%Determinarea k si k0 in cazul in care toate starile sunt masurabile
%Filtrul Kalman lipseste)
disp('Etapa I'
disp('Determinarea k si k0 in cazul in care toate starile sunt masurabile'
disp( (Filtrul Kalman lipseste)'
disp(
Ctheta=[0 0 0 1 0];
Arond=[Ar zeros(5,1); -Ctheta 0];
Brond=[Br;0];
disp('Ponderile se aleg ca fiind:'
Q=eye(6);
R=1;
%[k,x]=lgr(A,B,Q,R);
[krond,x]=lqr(Arond,Brond,Q,R);
k=-krond(:,1:5);
k0=-krond(:,6);
disp('k='); disp(k);
disp('k0='); disp(k0);
%Verificare Re(Lambda(Arond-Brond*krond))<0
disp('Partea reala a valorilor proprii ale (Arond-Brond*krond))'
disp(real(eig(Arond-Brond*krond))');
%raspunsul sistemului la treapta unitate
plot(step(Arond-Brond*krond,[0 0 0 0 0 1]',[0 0 0 1 0 0],0));
title('bf Raspunsul la comanda treapta unitate in cazul masurarii tuturor starilor'
grid on
figure;
%raspunsul sistemului la impuls Dirac
plot(impulse(Arond-Brond*krond,[0 0 0 0 0 1]',[0 0 0 1 0 0],0));
title('bf Raspunsul la comanda impuls Dirac in cazul masurarii tuturor starilor'
grid on
figure;
%ETAPA II
%(Filtrul Kalman)
disp('Etapa II'
disp('Calculul Filtrului Kalman '
disp(
Cr=[zeros(3,1) eye(3) zeros(3,1)];
Dr=zeros(3,1);
disp('Ponderile se aleg ca fiind:'
Q=1e-3
R=eye(3)*1e-3;
%Calculul filtrului Kalman
[L,P,E]=lqe(Ar,Br,Cr,Q,R);
AFK=Ar-L*Cr;
disp('Filtrul Kalman este (Ar-L*Cr)'
disp(AFK);
L
%Verificare Re(Lambda(Ar-L*Cr))<0
disp('Partea reala a valorilor proprii ale lui AFK =(Ar-L*Cr)'
disp(real(eig(Ar-L*Cr))');
t=0:1:200;
%zgomote:
d1=sqrt(1e-3)*randn(201,1);
d2=sqrt(1e-3)*randn(201,1);
d3=sqrt(1e-3)*randn(201,1);
d4=sqrt(1e-3)*randn(201,1);
plot(t,d1);
title('bf Zgomotul d_1=d_1(t)'
xlabel('t [s]'
ylabel('d_1'
grid on
%Alocam o comanda treapta unitate inainte de zgomot
u=ones(201,1)+d1;
figure;
plot(t,u);
axis([0 200 0 2]);
title('bf Comanda treapta unitate'
xlabel('t [s]'
ylabel('u'
grid on
%Calculul iesirilor u, nz, q si theta
V=lsim(Ar,Br,[1 0 0 0 0],0,u,t);
nz=lsim(Ar,Br,[0 1 0 0 0],0,u,t);
q=lsim(Ar,Br,[0 0 1 0 0],0,u,t);
theta=lsim(Ar,Br,[0 0 0 1 0],0,u,t);
%iesiri murdarite
nzm=nz+d2;
qm=q+d3;
thetam=theta+d4;
%viteza estimata este
Ve=lsim(AFK,[Br,L],[1 0 0 0 0],0,[u nzm qm thetam],t);
figure;
plot(t,V, ,t,Ve,'-o'
title('bf Viteza estimata vs. viteza reala'
xlabel('t [s]'
ylabel('V [m/s]; V_e [m/s]'
legend('V' 'Ve'
grid on
%comparatie intre q real, q perturbat si q estimat
%q estimat este
qe=lsim(AFK,[Br L],[0 0 1 0 0],0,[u nzm qm thetam],t);
figure;
plot(t,q,t,qm,t,qe,
title('bf q real vs. q perturbat vs. q estimat'
xlabel('t [s]'
ylabel('q; q_m; q_e'
legend('q' 'q_m' 'q_e'
grid on
%masurarea lui theta pentru diferite cazuri
%simulare fara zgomote
u=ones(201,1);
V=lsim(Ar,Br,[1 0 0 0 0],0,u,t);
nz=lsim(Ar,Br,[0 1 0 0 0],0,u,t);
q=lsim(Ar,Br,[0 0 1 0 0],0,u,t);
theta=lsim(Ar,Br,[0 0 0 1 0],0,u,t);
theta_e1=lsim(AFK,[Br,L],[0 0 0 1 0],0,[u nz q theta],t);
%simulare cu zgomote asupra iesirilor
nzm=nz+d2;
qm=q+d3;
thetam=theta+d4;
theta_e2=lsim(AFK,[Br,L],[0 0 0 1 0],0,[u nzm qm thetam],t);
%simulare cu zgomote asupra iesirilor masurate si comenzii
um=u+d1;
theta_e3=lsim(AFK,[Br,L],[0 0 0 1 0],0,[um nzm qm thetam],t);
figure;
plot(t,theta_e1,'k',t,theta_e2, ,t,theta_e3,'-o'
title('bf simulare cu/fara existenta zgomotelor'
xlabel('t [s]'
ylabel('theta_e [rad]'
legend('theta_e_1' 'theta_e_2' 'theta_e_3'
grid on
%Raspunsul pilotului automat la comanda treapta unitate si impuls Dirac
%Matricea de stabilitate a pilotului automat este
disp('Matricea de stabilitate a avionului cu pilotul automat cuplat:'
A_pa=[
Ar Br*k Br*k0;
L*Cr Ar-L*Cr+Br*k Br*k0;
-Ctheta zeros(1,5) 0]
%Matricea de comanda a pilotului automat este:
disp('Matricea de comanda a avionului cu pilotul automat cuplat:'
B_pa=zeros(11,1);
B_pa(11,1)=1;
disp('B_pa='
disp(B_pa);
%Verificare Re(Lambda(Ar-L*Cr))<0
disp('Partea reala a valorilor proprii A_pa'
disp(real(eig(A_pa))');
%comanda treapta unitate
figure;
plot(step(A_pa,B_pa,[Ctheta zeros(1,6)],0));
title('bf Raspunsul sistemului la comanda treapta unitate'
xlabel('t [s]'
ylabel('amplitudinea'
grid on
%comanda impuls Dirac
figure;
plot(impulse(A_pa,B_pa,[Ctheta zeros(1,6)],0));
title('bf Raspunsul sistemului la impuls Dirac'
xlabel('t [s]'
ylabel('amplitudinea'
grid on
%comanda delta_e
figure;
plot(step(A_pa,B_pa,[zeros(1,5) k k0],0));
title('bf Variatia in timp a comenzii delta_e'
xlabel('t [s]'
ylabel('amplitudinea'
grid on
%METODA H-infinit
disp('METODA H_INFINIT'
disp(
w=100; %ponderea erorii (theta_c-theta)
%x=Ax+B_1 u_1+B_2 u_2
A=[Ar zeros(5,1);
-Ctheta 0 ];
B_1=[Br*[0 1 0 0 0 0]; 1 0 0 0 0 0];
B_2=[Br;0];
%y_1=C_1 x+D_11 u_1+D_12 u_2
C_1=[-w*Ctheta 0;
0 0 0 0 0 1];
D_11=zeros(2,6);D_11(1,1)=w;
D_12=[0; 1];
%y_2=C_2 x+D_21 u_1+D_22 u_2
C_2=[zeros(2,6);zeros(3,1) eye(3) zeros(3,2)];C_2(2,6)=1
D_21=[zeros(2,6); zeros(3,2) eye(3) zeros(3,1)];D_21(1,1)=1;D_21(2,6)=1;
D_22=zeros(5,1);
%Aplicarea procedurii 'hinfsyn'
%[k,g,gfin,ax,ay,hamx,hamy]=
%hinfsyn(p,nmeas,ncon,gmin,gmax,tol,ricmethd,epr,epp)
p=[A B_1 B_2;
C_1 D_11 D_12;
C_2 D_21 D_22];
nmeas=5; %numarul de linii al matricei C_2
ncon=1; %numarul de coloane al matricei
gmin=1; %valoarea minima a lui gamma
gmax=1000; %valoarea maxima alui gamma
tol=.1; %diferenta relativa intre valorile gamma finale
ric=2; %ecuatia Riccati rezolvata cu metoda Schur
p=pss2sys(p,6);
minfo(p);
seesys(p);
[k,g]=hinfsyn(p,nmeas,ncon,gmin,gmax,tol,ric);
[A_H,B_H,C_H,D_H]=unpck(g);
disp('Pilotul automat:'
A_H
B_H
C_H
D_H
%raspunsul in timp la comanda treapta
figure;
sistem_Hinfinit=ss(A_H,B_H(:,1),C_H(1,:),D_H(1,1));
[theta,t]=step(sistem_Hinfinit);
theta=theta/w;
theta=1-theta;
plot(t,theta);
title('bf Raspunsului sistemului la comanda treapta unitate'
xlabel('t [s]'
ylabel('Theta [rad]'
grid on
figure;
[theta,t]=impulse(sistem_Hinfinit);
theta=theta/w;
%theta=1-theta;
plot(t,theta);
title('bf Raspunsului sistemului la comanda impuls Dirac'
xlabel('t [s]'
ylabel('theta [rad]'
grid on
disp('Valorile proprii ale sistemului (avion cu pilot automat cuplat) rezultant sunt:'
disp(eig(A_H));
2.4 Rezultatul programului de proiectare a pilotului automat pentru unghiul de atitudine longitudinala
Proiectarea pilotului automat pentru unghiul de atitudine longitudinala
knz =
kq =
Partea reala a valorilor proprii ale lui Ar
Metoda conventionala
Etapa I
Determinarea k si k0 in cazul in care toate starile sunt masurabile
(Filtrul Kalman lipseste)
Ponderile se aleg ca fiind:
k=
k0=
Partea reala a valorilor proprii ale (Arond-Brond*krond))
Etapa II
Calculul Filtrului Kalman
Ponderile se aleg ca fiind:
Q =
1.0000e-003
Filtrul Kalman este (Ar-L*Cr)
0 -0.0001 1.0000 -0.0007 0
L =
Partea reala a valorilor proprii ale lui AFK =(Ar-L*Cr)
Matricea de stabilitate a avionului cu pilotul automat cuplat:
A_pa =
Columns 1 through 10
Column 11
Matricea de comanda a avionului cu pilotul automat cuplat:
B_pa=
Partea reala a valorilor proprii A_pa
Columns 1 through 10
Column 11
METODA H_INFINIT
C_2 =
system: 6 states 7 outputs 7 inputs
-8.5e-003 3.7e+001 2.3e+001 -9.8e+000 -2.3e+000 0.0e+000 | 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
-2.1e-004 -6.9e-001 8.4e-001 2.0e-004 1.5e-002 0.0e+000 | 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
-3.8e-005 -9.8e+000 -4.2e+000 0.0e+000 4.0e-001 0.0e+000 | 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
0.0e+000 0.0e+000 1.0e+000 0.0e+000 0.0e+000 0.0e+000 | 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
0.0e+000 0.0e+000 0.0e+000 0.0e+000 -4.0e+000 0.0e+000 | 0.0e+000 1.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 1.0e+000
0.0e+000 0.0e+000 0.0e+000 -1.0e+000 0.0e+000 0.0e+000 | 1.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
0.0e+000 0.0e+000 0.0e+000 -1.0e+002 0.0e+000 0.0e+000 | 1.0e+002 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 1.0e+000 | 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 1.0e+000
0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 | 1.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 1.0e+000 | 0.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 1.0e+000 0.0e+000
0.0e+000 1.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000 | 0.0e+000 0.0e+000 1.0e+000 0.0e+000 0.0e+000 0.0e+000 0.0e+000
0.0e+000 0.0e+000 1.0e+000 0.0e+000 0.0e+000 0.0e+000 | 0.0e+000 0.0e+000 0.0e+000 1.0e+000 0.0e+000 0.0e+000 0.0e+000
0.0e+000 0.0e+000 0.0e+000 1.0e+000 0.0e+000 0.0e+000 | 0.0e+000 0.0e+000 0.0e+000 0.0e+000 1.0e+000 0.0e+000 0.0e+000
Resetting value of Gamma min based on D_11, D_12, D_21 terms
Test bounds: 100.0000 < gamma <= 1000.0000
gamma hamx_eig xinf_eig hamy_eig yinf_eig nrho_xy p/f
1.000e+003 5.3e-003 7.6e-004 3.5e-003 1.5e-003 0.0000 p
550.000 5.3e-003 7.7e-004 3.5e-003 1.5e-003 0.0001 p
325.000 5.2e-003 8.1e-004 3.5e-003 1.5e-003 0.0005 p
212.500 5.1e-003 -1.2e+003# 3.5e-003 1.5e-003 0.0009 f
268.750 5.2e-003 8.5e-004 3.5e-003 1.5e-003 0.0041 p
240.625 5.1e-003 -5.1e+003# 3.5e-003 1.5e-003 0.0020 f
254.688 5.1e-003 -2.3e+004# 3.5e-003 1.5e-003 0.0073 f
261.719 5.1e-003 8.5e-004 3.5e-003 1.5e-003 0.0189 p
258.203 5.1e-003 -7.8e+004# 3.5e-003 1.5e-003 0.0237 f
259.961 5.1e-003 8.5e-004 3.5e-003 1.5e-003 0.1937 p
259.082 5.1e-003 -1.8e+005# 3.5e-003 1.5e-003 0.0538 f
259.521 5.1e-003 -5.0e+005# 3.5e-003 1.5e-003 0.1488 f
259.741 5.1e-003 -4.3e+006# 3.5e-003 1.5e-003 1.2781# f
259.851 5.1e-003 8.6e-004 3.5e-003 1.5e-003 0.4568 p
259.796 5.1e-003 8.6e-004 3.5e-003 1.5e-003 1.4219# f
Gamma value achieved: 259.8511
Pilotul automat:
A_H =
1.0e+004 *
Columns 1 through 10
Columns 11 through 12
B_H =
C_H =
1.0e+003 *
Columns 1 through 10
Columns 11 through 12
D_H =
Valorile proprii ale sistemului (avion cu pilot automat cuplat) rezultant sunt:
-1.8667 + 3.1283i
-1.8667 - 3.1283i
-2.4541 + 2.2678i
-2.4541 - 2.2678i
-0.0297 + 0.0509i
-0.0297 - 0.0509i
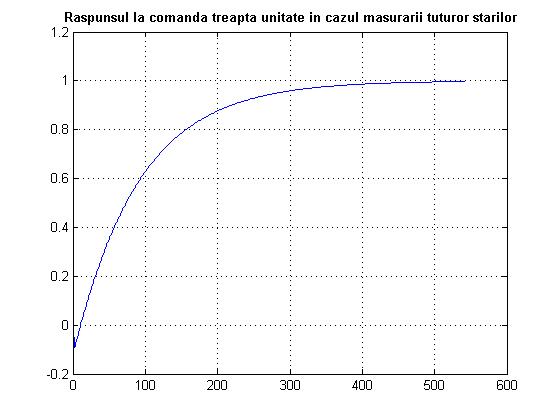
Fig. 2.8
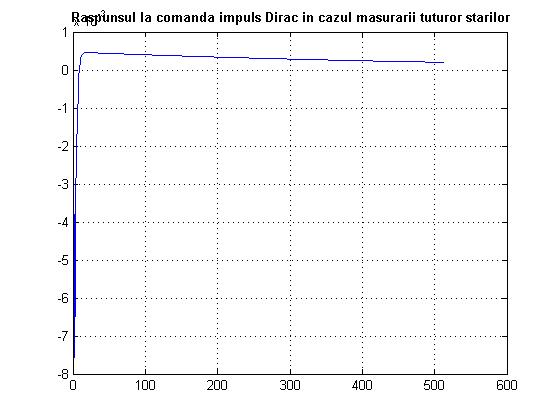
Fig. 2.9
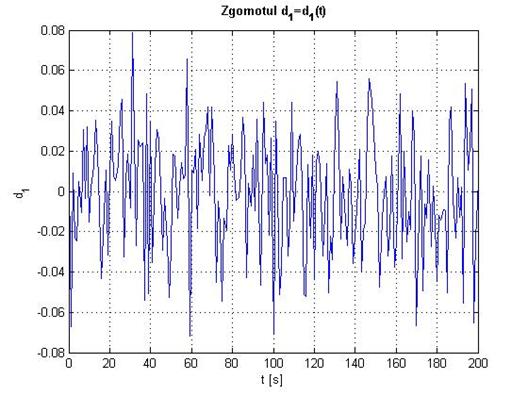
Fig. 2.10
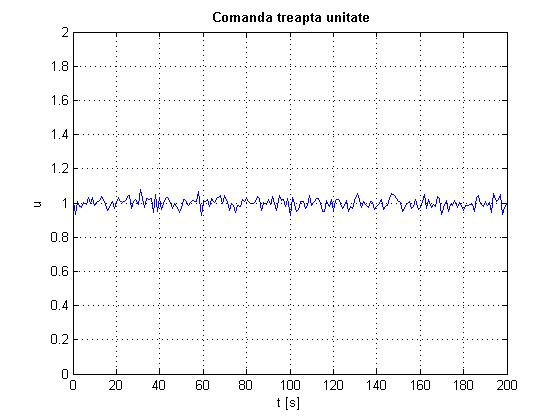
Fig. 2.11
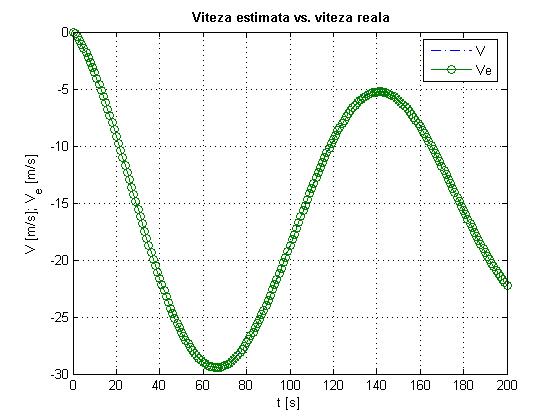
Fig. 2.12
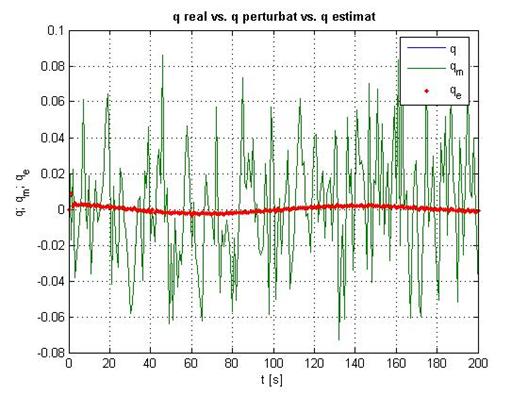
Fig. 2.13
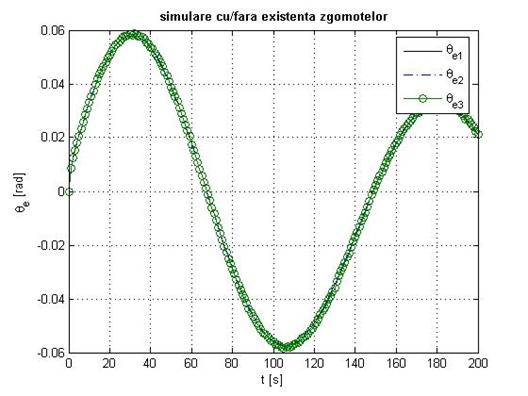
Fig. 2.14
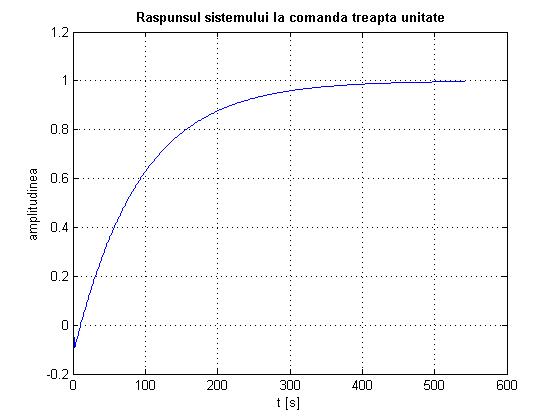
Fig 2.15
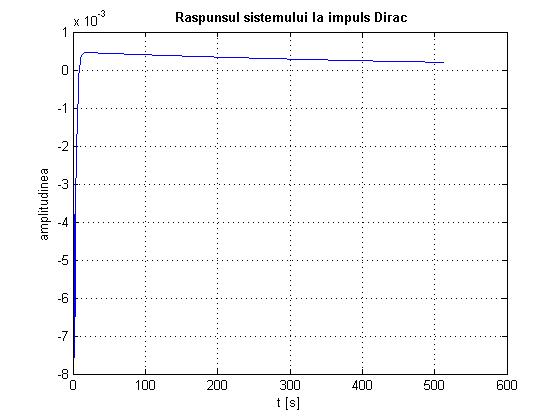
Fig. 2.16
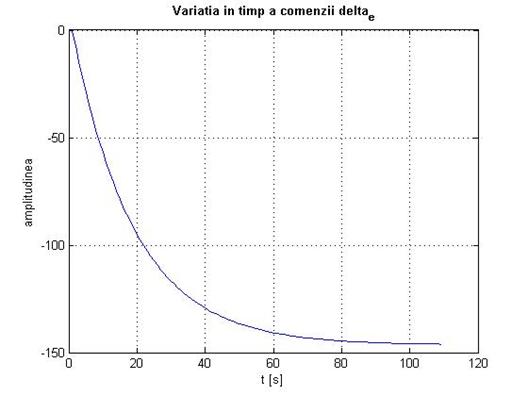
Fig. 2.17
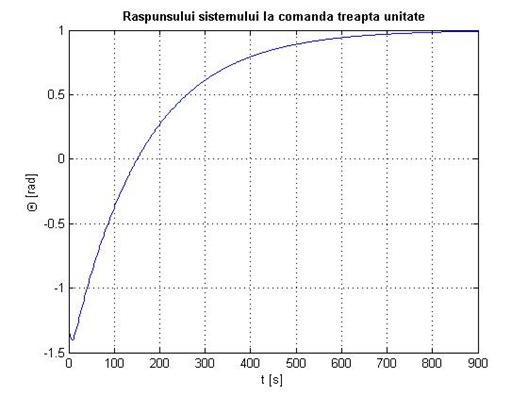
Fig. 2.18
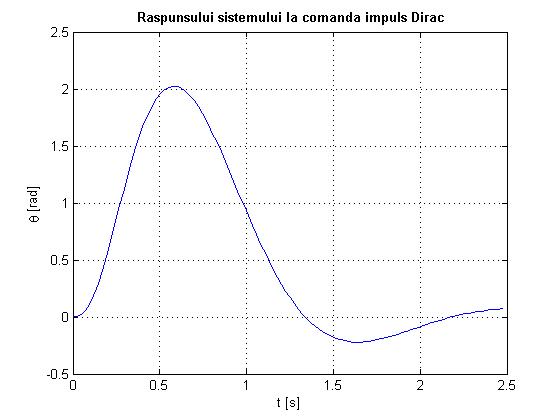
Fig. 2.19