METODE SI TEHNICI DE STABILIRE A TARIFELOR DE PRIME LA ASIGURARILE DE VIATA

Metode si tehnici de stabilire a TARIFELOR DE PRIME la asigurarile de viata

INTRODUCERE

Asigurarile de viata presupun preluarea riscurilor cu care se confrunta persoana fizica a asiguratului (vatamare corporala, deces, supravietuire, imbolnavire) de catre societatea de asigurari in schimbul primei de asigurare. Daca are loc producerea riscului asigurat atunci asiguratorul se obliga la plata sumei asigurate aferenta contractului.

PREZENTAREA TEMEI

Fata de asigurarile de bunuri, la care scopul consta in refacerea valorii bunului de dinainte de producerea riscului asigurat, asigurarile de persoane urmaresc fructificarea capitalurilor persoanelor asigurate.

Facand o comparatie intre asigurarile de bunuri si cele de persoane se constata urmatoarele diferente :

º suma asigurata in cazul asigurarilor de bunuri este limitata la valoarea reala a bunului pe cand in cazul asigurarilor de persoane asiguratul stabileste suma asigurata in functie de puterea de cumparare sau, daca are loc producerea riscului asigurat atunci asiguratorul va plati asiguratului o despagubire care nu poate depasi paguba in cazul asigurarilor de bunuri iar in situatia asigurarilor de persoane, suma asigurata;

º in situatia in care asiguratul incheie mai multe asigurari pentru acelasi bun atunci despagubirea incasata de la toti asiguratorii nu va fi mai mare decat valoarea pagubei, pe cand in asigurarile de persoane, asiguratul poate contracta oricate asigurari doreste primind de la toate societatile de asigurari sumele asigurate fara nici o restrictie;

º prima de asigurare pentru asigurarile de bunuri se stabileste in functie de probabilitatile de aparitie a riscului fara sa se tina seama de varsta asiguratului;

ºin asigurarile de persoane primele se stabilesc prin calcule actuariale plecand de la probabilitatile de supravietuire sau de deces in legatura cu varsta persoanei asigurate.

Unul din criteriile in functie de care se realizeaza clasificarea asigurarilor de viata este riscul a sigurat iar in raport cu acesta avem urmatoarea grupare :

º asigurari de supravietuire;

º asigurari de deces;

º asigurari de accidente.

1. Stabilirea primei de asigurare in asigurarile de supravietuire

Asigurarile de supravietuire au ca obiect riscul de supravietuire a asiguratului la un moment dat. Intr-un astfel de contract asiguratul se obliga la plata primelor de asigurare fie dintr-o data la momentul semnarii contractului fie esalonat pe o anumita perioada de timp.

De asemenea, societatea de asigurari are posibilitatea de a plati suma asigurata fie dintr-o data la scadenta daca asiguratul este in viata fie periodic in timp, pe parcursul duratei de viata.

In general, in toate tipurile de asigurari de supravietuire, societatea de asigurari plateste atata timp cat asiguratul este in viata; in caz contrar asiguratorul este exonerat de orice obligatie.

Daca asiguratul decedeaza inainte de expirarea contractului si pierde astfel o parte importanta din suma asigurata atunci acesta are posibilitatea de a inscrie in contract clauza denumita contraasigurare care presupune rambursarea unei parti din sumele platite de asigurat.

La baza stabilirii primelor in cazul asigurarilor de viata stau urmatoarele principii:

º principiul echivalentei sarcinilor;

º principiul aditivitatii primelor.

In conformitate cu principiul echivalentei sarcinilor operatiunea de asigurare este echitabila daca valoarea actuala probabila la momentul semnarii contractului este aceeasi atat pentru asigurat cat si pentru asigurator.

Cel de-al doilea principiu consfinteste faptul ca, daca printr-un contract de asigurare se asigura mai multe riscuri atunci prima achitata de asigurat este egala cu suma primelor aferente fiecarui risc asigurat.

Actuarii au realizat o clasificare a indivizilor in grupe omogene care prezinta, cu exceptia varstei riscuri identice. Omogenitatea este relativa depinzand de parametrii luati in considerare, persoanele care fac parte dintr-un grup pot fi deosebite in mod sigur dupa varsta, ceilalti factori fiind greu de evaluat.

Punctul de plecare in determinarea primelor aferente asigurarilor de persoane este reprezentat de functiile biometrice.

O prima functie biometrica care se regaseste in tabelele de mortalitate specifice fiecarei tari este functia de supravietuire.

Acesta se noteaza cu lx si reprezinta numarul mediu de persoane aflate in viata dintr-o populatie omogena la varsta de x ani. Se noteaza cu varsta maxima pe care o atinge o persoana, iar in asigurari aceasta are valoarea de 100 de ani.

Astfel, se considera ca varsta de 100 de ani nu este atinsa de nici o persoana din populatia respectiva, adica l

Cea de-a doua functie biometrica este probabilitatea de viata sau de supravietuire p(x,y) si reprezinta probabilitatea ca o persoana in varsta de x ani sa fie in viata la implinirea varstei de y ani.

O probabilitate in caz discret se calculeaza ca raport intre numarul de cazuri favorabile si numarul de cazuri posibile:

Probabilitatea de viata se poate exprima in raport cu functia de supravietuire dupa urmatoarea formula :

In calculele actuariale se utilizeaza urmatoarea forma pentru probabilitatea de viata:

unde _n p _x este probabilitatea unei persoane in varsta de x ani sa fie in viata peste n ani sau la varsta de x + n ani.

O alta functie biometrica necesara fundamentarii tarifelor de prime este probabilitatea de moarte sau de deces.

Se noteaza cu q(x,y) si reprezinta probabilitatea ca o persoana in varsta de x ani sa nu mai fie in viata la varsta de y ani.

Probabilitatea de moarte imbraca urmatoarele forme :

q(x,y)=1-p(x,y), sau q(x,y)=1-, sau _nq_x=1-

unde _nq_x reprezinta probabilitatea ca o persoana in varsta de x ani sa nu mai fie in viata peste n ani sau la implinirea varstei de x+n ani.

Functiile biometrice prezinta o importanta deosebita deoarece stau la baza determinarii primelor de asigurare. Acestea, in principiu, se gasesc in tabelele de mortalitate construite in fiecare tara si sunt influentate de specificul populatiei locale.

Astfel societatile de asigurare cu capital strain trebuie sa-si adapteze calculele actuariale si sa ia in considerare tabelele de mortalitate din Romania. In tara noastra primul tabel a aparut in 1990 dupa recensamantul din acel an si s-a datorat lui N Proporgescu si N. Stanielevici.[1]

Cred ca pentru o mai buna fundamentare a tarifelor de prime si implicit pentru diminuarea riscului de neplata a sumelor asigurate la scadenta contractelor, este necesar ca aceste tabele sa fie reinoite periodic si chiar sa se faca previziuni pentru perioadele urmatoare deoarece asigurarile de viata sunt incheiate pe intervale lungi de timp (zeci de ani) in care pot aparea mutii considerabile.

In functie de modul de plata a sumei asigurate, asigurarile de supravietuire se grupeaza astfel :

º asigurari de supravietuire cu plata unica;

º asigurari de supravietuire cu plata anuala;

º asigurari de supravietuire cu plata fractionata.

1.1. Stabilirea primei nete unice in asigurarile de supravietuire cu plata unica

Aceasta categorie de asigurari se caracterizeaza prin faptul ca asiguratorul plateste o singura suma la scadenta daca asiguratul este in viata.

Sa presupunem ca avem o persoana in varsta de x ani ce contracteaza o asigurare de supravietuire prin care urmeaza sa primeasca peste n ani (la implinirea varstei de x + n ani) suma de S u.m. daca este in viata, in caz contrar societatea de asigurari este absolvita de orice obligatie.

Notam cu i procentul mediu anual al pietei caracteristic perioadei de timp pentru care s-a incheiat contractul de asigurare.

Daca operatiunea financiara dintre cele doua parti contractante ar fi certa atunci am avea de-a face cu un proces de fructificare a capitalului in sistem de dobanda compusa.

Deoarece in cazul asigurarilor de supravietuire societatea de asigurari isi onoreaza obligatia de plata doar atunci cand asiguratul este in viata, factorul de actualizare viager utilizat in teoria asigurarilor are urmatoarea forma :

_nE_x =_np_x∙vⁿ, unde v=

Prima neta unica (P_nu) platita de asigurat la momentul semnarii contractului se determina pe baza principiului valorii actuale probabile sau al echivalentei sarcinilor.

Notam cu VAP(a) = valoarea actuala probabila a asiguratului si cu VAP(A) = valoarea actuala probabila a asiguratorului.

La momentul initial VAP(a) = P_nu deoarece, prima neta unica este achitata de asigurat odata cu semnarea contractului.

In cazul asiguratorului VAP(A) = S . _nE_x , unde S este valoarea sumei asigurate.

Astfel prima neta unica este P_nu = S . nEx

Factorul de actualizare viager (_nE_x) se poate exprima in raport cu numerele de comutatie D_x dupa urmatoarea formula:

_nE_x =, unde D_x= v^x ∙l_x

Asadar in functie de numerele de comutatie prima neta unica aferenta unei asigurari de supravietuire cu plata unica se poate exprima astfel:

P_nu = S .

Numerele de comutatie D_x sunt tabelate pentru toate varstele la un procent i dat.

Sa consideram o persoana in varsta de 23 de ani ce incheie o asigurare de supravietuire pe termen de 15 de ani prin care urmeaza sa primeasca la scadenta suma de 800 000 de u.m., daca este in viata. Pentru aceasta asiguratul trebuie sa achite o prima neta unica in valoare de 184.696,27 u.m. deoarece :

P_nu =800.000, unde D₃₈ = 2.459, iar D₂₃ = 10.651, P_nu = 184.696,27 u.m

Numerele de comutatie utilizate in calcule sunt determinate cu procentul de i = 10%.

1.2. Stabilirea primei nete unice in asigurarile de supravietuire cu plata anuala

Asigurarile de supravietuire prezinta o larga diversitate din punct de vedere al modului de plata a obligatiilor partilor contractante.

Daca ne referim la obligatia de plata a asiguratorului, exista numeroase situatii in care societatea de asigurari achita asiguratului mai multe sume asigurate la momente diferite, la inceputul sau la sfarsitul anului pe anumite perioade de timp.

Astfel, in cazul in care plata sumelor asigurate se efectueaza anual atunci acestea se numesc anuitati si imbraca urmatoarele forme :

º anuitati imediate nelimitate;

º anuitati imediate limitate;

º anuitati amanate nelimitate;

º anuitati amanate limitate.

Pentru fiecare categorie de anuitati urmarim sa determinam prima neta unica platita de asigurat.

Printr-o anuitate imediata nelimitata, asiguratul in varsta de x ani urmeaza sa primeasca, din momentul semnarii contractului pe toata durata vietii o suma asigurata de S u.m. care poate fi achitata anticipat (la inceputul fiecarui an) sau posticipat (la sfarsitul fiecarui an).

Daca consideram ca suma asigurata incasata de asigurat este de 1 u.m., atunci prima neta se numeste prima neta unitara si se noteaza cu , sau in functie de momentul la care se face plata sumelor asigurate, la inceputul sau la sfarsitul anului.

Se noteaza cu:

N_x= si reprezinta un alt numar de comutatie utilizat in asigurarile de supravietuire.

Folosind cele doua principii prezentate anterior, si anume, principiul echivalentei sarcinilor si cel al aditivitatii primelor, prima neta unica unitara are urmatoarea forma :

a= in cazul anticipat si a= in cazul posticipat.

Deci prima neta unica aferenta unui contract de asigurare incheiat pentru o suma asigurata de S u. m. este :

P_nu = S sau P_nu = S . in cazul anticipat, si P_nu = S sau P_nu = S . in cazul posticipat.

Cazul posticipat consta in faptul ca sumele asigurate sunt platite la sfarsitul anului. In general, cazul posticipat difera de cel anticipat prin translatarea indicilor de la numarator cu 1.

In cazul in care contractul de asigurare pentru care opteaza pentruo anuitate imediata limitata, atunci societatea de asigurari este obligata la plata sumei asigurate la inceputul sau sfarsitul fiecarui an pana la o anumita varsta x + n.

Prima neta unica unitara se noteaza cu:

            in cazul anticipat sau in cazul posticipat, unde n este durata asigurarii.

Formula obtinuta pentru prima neta unica unitara pe baza calculelor actuariale este urmatoarea:

Cazul anticipat P_nu=S∙ sau P_nu=S∙

Cazul posticipat P_nu=S∙sau P_nu=S∙

Unul dintre cele mai utilizate produse de asigurare este asigurarea de tip pensie viagera. Un astfel de produs poate fi considerat anuitatea amanata nelimitata care presupune plata sumelor asigurate la inceputul sau la sfarsitul fiecarui an incepand cu o anumita varsta, pe toata durata vietii.

Notam cu _r sau _rprima neta unica unitara pentru o anuitate amanata nelimitata anticipata sau posticipata. Daca asiguratul are varsta de x ani iar asiguratorul incepe sa achite sumele asigurate de la varsta de x + r ani atunci valoarea primei de asigurare este:

Cazul anticipat P_nu=S∙ _rsau P_nu=S∙ sau Cazul posticipat P_nu=S∙ _rsau P_nu=S∙

Anuitatea amanata limitata presupune ca asiguratorul sa plateasca incepand cu o anumita varsta, pe o perioada determinata de timp, la inceputul sau la sfarsitul fiecarui an, suma asigurata.

Se noteaza cu _r sau _r prima neta unica unitara pentru o anuitate amanata limitata anticipata sau posticipata.

O persoana in varsta de x ani incheie o asigurare prin care urmeaza sa primeasca peste r ani (la implinirea varstei de x+r ani) timp de n ani (pana la varsta de x + r + n ani) la inceputul sau la sfarsitul fiecarui an suma de S u.m.

Prima neta unica pe care o datoreaza asiguratul la momentul contractarii asigurarii imbraca urmatoarea forma in functie de momentul platii:

Cazul anticipat P_nu=S∙ _rsau P_nu=S∙

Cazul posticipat P_nu=S∙ _rsau P_nu=S∙

Sa consideram o persoana in varsta de x = 25 ani care procura o asigurare de supravietuire prin care societatea de asigurari ii plateste suma de S = 500 000 u. m.

a. la inceputul fiecarui an, cat timp va trai;

b. sau la sfarsitul fiecarui an, cat timp va trai.

Utilizand numerele de comutatie N₂₅ = 92 317 ; N₂₆ = 83 540, D₂₅ = 8 777 atunci prima neta unica datorata de asigurat este:

a. Cazul anticipat: P_nu =500000= 5259029,28 u.m.

b. Cazul posticipat: P_nu =500000= 4759029,28 u.m.

Numerele de comutatie utilizate in calcule sunt determinate cu procentul de i = 10%.

1. Stabilirea primei nete unice in asigurari de supravietuire cu plata fractionata

Aceste categorii de asigurari presupun impartirea anului financiar in m fractiuni si plata sumelor asigurate la inceputul sau la sfarsitul fiecarei fractiuni de timp.

Pentru:

ºm = 12 plata se efectueaza lunar;

º m = 4 plata se face trimestrial;

º m = 2 plata se realizeaza semestrial;

Deoarece plata sumelor asigurate este realizata fractionat in timp, aceste asigurari se mai numesc si fractionalitati.

Clasificarea fractionalitatilor se face analog cu cazul anuitatilor si anume:

º fractionalitati imediate nelimitate;

º fractionalitati imediate limitate;

º fractionalitati amanate nelimitate;

º fractionalitati amanate limitate.

Fractionalitatile imediate nelimitate se caracterizeaza prin faptul ca asiguratul va incasa suma asigurata la inceputul sau la finele fiecarei fractiuni din an, pe toata durata vietii.

Notam cu sau cu a prima neta unica unitara pe care o datoreaza asiguratul pentru primirea unei unitati monetare la inceputul sau la sfarsitul fiecarei fractiuni din an.

Pentru o persoana in varsta de x ani ce incheie o astfel de asigurare, la o suma asigurata de S u.m., prima neta unica pe care o plateste societatii de asigurarii are urmatoarea forma:

Fractionalitatile imediate limitate unitare anticipate sau posticipate se noteaza cu:

sau unde m = 2; m = 4; m = 12

O astfel de asigurare incheiata de o persoana in varsta de x ani presupune ca asiguratul sa primeasca din partea asiguratorului o suma de S u.m. in fiecare fractiune din an, timp de n ani sau pana la varsta de x + n ani.

Formulele de calcul pentru acest tip de fractionalitate sunt urmatoarele:

Cazul anticipat:

= - = -

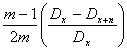
P_nu = m ∙ S∙

P_nu = m ∙ S∙-

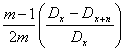
Cazul posticipat

= + = +

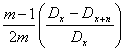
P_nu = m ∙ S∙

P_nu = m ∙ S∙+

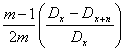
In cazul fractionalitatilor amanate nelimitate asiguratul in varsta de x ani incaseaza suma de S u.m. incepand cu varsta de x + r ani la inceputul sau la sfarsitul fiecarei fractiuni din an, pe toata durata vietii.

Notam cu si cu prima neta unica unitara pentru o fractionalitate amanata nelimitata anticipata sau posticipata.

Prima neta unica poate imbraca una din urmatoarele forme:

Fractionalitatile amanate limitate presupun ca, un asigurat in varsta de x ani sa incaseze suma asigurata in valoare de S u.m. la inceputul sau la sfarsitul fiecarei fractiuni din an, incepand cu varsta de x + r ani, timp de n ani (pana la varsta de x + r + n ani):

Se noteaza cu si cu prima neta unica unitara in cazul unei fractionalitati, amanate, limitate, anticipate sau posticipate.

Acest tip de asigurare presupune in principiu, ca plata sumei asigurate sa se faca incepand cu o anumita varsta, pe o perioada determinata de timp, formulele pentru prima neta unica fiind urmatoarele:

Daca avem o persoana in varsta de 30 de ani ce incheie o asigurare prin care primeste timp de 10 ani

a. la inceputul fiecarei luni (m = 12);

b. la sfarsitul fiecarui trimestru (m = 4);

suma de 500 000 u.m., atunci prima neta unica inregistreaza urmatoarele valori:

a. Cazul anticipat si m = 12: P_nu = 12 ∙ 500 000 ∙ 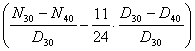P_nu = 38421154,5 u.m

b. Cazul posticipat si m = 4: P_nu = 4 ∙ 500 000 ∙ 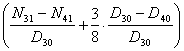P_nu = 12597908 u.m

Numerele de comutatie utilizate in calcule sunt determinate cu procentul de i = 10%.

2. Stabilirea primei nete unice in asigurari de deces

Decesul este singurul eveniment cert asigurat, incertitudinea fiind in acest caz momentul la care el se produce.

Asigurarile de deces presupun ca pe perioada contractului

de asigurare, in caz de deces al asiguratului, societatea de asigurari sa plateasca suma asigurata urmasilor acestuia.

La scadenta contractului, daca asiguratul este in viata si daca evenimentul asigurat nu s-a produs atunci asiguratorul este exonerat de orice obligatie.

Protectia prin asigurare incepe odata cu plata primei de asigurare.

Prima neta unica se stabileste in functie de caracteristicile fiecarui contract, pe baza calculelor actuariale, avandu-se in vedere elemente generale ca: statistici, tabele de mortalitate etc.

In functie de momentul intrarii in vigoare si de durata contractului de asigurare, asigurarile de deces se clasifica astfel:

Æ asigurari de deces imediate nelimitate;

Æ asigurari de deces imediate limitate;

Æ asigurari de deces amanate nelimitate;

Æ asigurari de deces amanate limitate.

Prima neta unica pentru o asigurare de deces imediata nelimitata incheiata de un individ in varsta de x ani la o suma asigurata de S u.m. este:

Pnu = S Ax sau Pnu = S

In cazul unui contract de asigurare de deces valabil o perioada limitata de timp asiguratorul va plati suma asigurata urmasilor numai daca decesul survine in perioada de valabilitate a contractului.

Notam cu _nprima neta unica unitara pentru o asigurare de deces incheiata de o persoana in varsta de x ani prin care urmasii vor primi suma de S u.m daca asiguratul nu mai este in viata peste n ani.

In cazul in care titularul contractului de asigurare supravietuieste pana la varsta de x + n ani, societatea de asigurari nu mai are nici un fel de obligatie financiara fata de acesta.

Prima neta unica unitara are urmatoarea forma:

=

Prima neta unica aferenta unei asigurari pentru o suma asigurata de S u.m. va fi:

P_nu=S sau P_nu=S

Asigurarea de deces amanata nelimitata se caracterizeaza prin faptul ca valabilitatea ei incepe peste o perioada determinata de timp.

Astfel o persoana in varsta de x ani ce incheie o asigurare de deces prin care urmasii urmeaza sa primeasca suma de S u.m. daca decesul sau se produce peste r ani atunci prima neta unica unitara _rsi prima neta unica imbraca urmatoarele forme:

_r=, iar P_nu=S _rsau P_nu=S

Asigurarea de deces amanata limitata presupune ca un individ in varsta de x ani sa incheie o asigurare prin care urmeaza ca urmasii sai sa primeasca, in cazul decesului sau, daca acesta intervine intre varstele de x + r ani si x + r + n ani, suma de S u.m.

Daca asiguratul decedeaza inainte de varsta de x + r ani sau este in viata la varsta de x + r + n ani, atunci societatea de asigurari nu mai are nici o obligatie fata de persoana asigurata sau fata de urmasii sai. Prima neta unica unitara are urmatoarea forma:

_r=,

Pentru o asigurare de deces amanata limitata prima neta unica aferenta sumei de S u.m. va fi:

P_nu=S _rsau P_nu=S

Asigurarea de deces valabila o perioada limitata de timp incheiata de o persoana in varsta de 25 de ani prevede ca in cazul decesului sau urmasii urmeaza sa primeasca suma de 500 000 u.m. daca acesta survine inainte de 45 de ani. Cunoscand valoarea numerelor de comutatie: M₂₅= 385, M₄₅=176, D₂₅=8777, pentru i=10%, putem determina prima neta unica pe care asiguratul trebuie sa o plateasca in acest caz, si anume: P_nu=500000= 11906,11 u.m

Stabilirea primei nete unice in asigurarile mixte de viata

Pana acum, riscurile de supravietuire si de deces au fost studiate separat prin tipurile de asigurari respective.

In cazul riscului de supravietuire, daca persoana asigurata deceda pe perioada contractului de asigurare, atunci societatea de asigurari era exonerata de orice obligatie fata de asigurat.

Deci in cazul decesului asiguratului, urmasii acestuia nu mai au dreptul de a mai incasa vreo suma de bani de la asigurator.

Oarecum asemanator stau lucrurile si in asigurarile de deces, in caz de supravietuire la termenul prevazut in contract, asiguratul nu mai are dreptul de a incasa suma asigurata.

In ambele situatii, asigurarile respective dau impresia ca una din partile implicate in asigurare, asiguratul sau asiguratorul, are de pierdut in urma producerii riscului asigurat.

In realitate insa, ambele asigurari sunt echitabile atat din punctul de vedere al asiguratului cat si al asiguratorului.

Asigurarile mixte inlatura aceasta impresie in legatura cu asigurarile de supravietuire si cele de deces asigurand ambele riscuri intr-un singur contract de asigurare.

De asemenea, asigurarile mixte lasa falsa impresie ca asiguratorul iese in pierdere deoarece indiferent de ce se intampla cu asiguratul acesta este obligat la plata unei sume de bani.

Aceasta afirmatie nu are suport real intrucat asiguratul plateste o prima neta unica ce reprezinta suma primelor aferente celor doua riscuri asigurate.

Principalele tipuri de asigurari mixte de viata cunoscute in practica asigurarilor sunt:

Æasigurari mixte generale;

Æasigurari mixte cu suma dubla;

Æasigurari mixte cu termen fix;

Æasigurari mixte cu termen fix si suma dubla.

Asigurarea mixta generala este incheiata pe o perioada determinata de timp si presupune ca societatea de asigurari sa plateasca asiguratului suma asigurata daca este in viata la scadenta politei iar daca a decedat inainte de acest termen, sa plateasca urmasilor sai o suma de bani.

O persoana in varsta de x ani care incheie o astfel de asigurare, urmeaza sa incaseze la implinirea varstei de x + n ani, daca este in viata suma de S₁ u.m. sau urmasii sai sa primeasca suma de S₂ u.m. daca decesul sau survine pana la varsta de x + n ani.

In acest caz, prima neta unica achitata de asigurat este egala cu suma primelor pentru o asigurare de supravietuire cu plata unica si una de deces imediata limitata.

Prima neta unica are urmatoarele forme:

P_nu= S_1∙nE_x+ S₂sau P_nu= S_{1∙ +} S₂

Daca cele doua sume asigurate sunt egale atunci prima neta unica este:

P_nu= S_∙(_nE_x+ )sau P_nu= S_{∙( + )}

Asigurarea mixta cu suma dubla presupune ca societatea de asigurari sa plateasca suma asigurata, urmasilor asiguratului indiferent de momentul decesului sau ori asiguratul sa incaseze suma asigurata daca este in viata la o varsta stabilita prin contract.

Printr-o astfel de asigurare, o persoana in varsta de x ani urmeaza sa incaseze suma de S₁ u.m. in cazul in care decesul sau survine inainte de varsta de x + n ani si suma de S₂ u.m. daca decesul are loc dupa varsta de x + n ani iar in cazul in care persoana asigurata este in viata la implinirea varstei de x + n ani acesta va primi suma de S3 u.m.

O astfel de asigurare este denumita cu suma dubla deoarece in situatia in care asiguratul supravietuieste pana la varsta de x+n ani, atunci societatea de asigurari este obligata la plata a doua sume asigurate, una fiind incasata de asigurat pentru ca a supravietuit pana la varsta de x + n ani si alta de urmasii sai la decesul sau.

Asigurarea mixta cu suma dubla este compusa dintr-o asigurare de deces limitata la n ani, o asigurare de supravietuire pe termen de n ani cu plata unica si o asigurare de deces amanata cu n ani.

In functie de cum sumele S1, S2 si S3 sunt diferite sau nu, prima neta unica imbraca urmatoarele forme:

a) daca S1 ≠S2 ≠S3 atunci: P_nu =S_1∙+ S₃ ∙_nE_x + S_{2 ∙} sauP_nu =S₃₊ S₁₊ S₂

b) daca S1 = S2 ≠S3 atunci: P_nu =S_1∙+ +S₃ ∙_nE_x sau P_nu =S₃₊ S₁

Am tinut cont de faptul ca: _{+ = += =}

c) daca S1 = S3 ≠S2 atunci avem: P_nu =S_{1∙+ n}E_x +S₂ ∙ sau P_nu =S₁₊ S₂

d) daca S1 ≠S2 = S3 atunci: P_nu =S_1∙+S₃ ∙_nE_{x +} sau P_nu =S₁₊ S₂

e) daca toate sumele sunt egale S1 = S2 = S3 = S atunci: P_nu =S_{∙+ n}E_{x +} sau P_nu = S∙(A_x+ _nE_x )

P_nu = S

Asigurarea mixta cu termen fix se deosebeste de celelalte tipuri de asigurari mixte prin faptul ca suma asigurata se plateste atat asiguratului daca este in viata cat si urmasilor acestuia in cazul decesului sau, la un moment dat, prevazut in polita de asigurare.

Astfel o persoana in varsta de x ani ce incheie o asigurare mixta cu termen fix, primeste peste n ani, suma de S u.m. daca este in viata sau urmasii sai primesc aceeasi suma de bani la acelasi moment daca decesul survine anterior.

Prima neta unica pentru o asigurare mixta cu termen fix este:

Pnu = S.vⁿ , unde v=, iar i este rata dobanzii

Asigurarea mixta cu termen fix si suma dubla este compusa dintr-o asigurare mixta cu termen fix si o asigurare de deces amanata nelimitata.

Acest tip de asigurare se caracterizeaza prin faptul ca urmasii primesc suma asigurata fie la momentul fixat prin contract daca decesul asiguratului survine anterior acestui moment, fie la momentul decesului daca acesta se intampla dupa termenul fixat.

Daca asiguratul este in viata la momentul stabilit prin polita de asigurare atunci acesta incaseaza suma asigurata.

Printr-o astfel de asigurare o persoana in varsta de x ani urmeaza sa incaseze peste n ani suma de S₁ u.m. daca este in viata, sau urmasii sai vor primi la acelasi moment, x + n, aceeasi suma daca decesul persoanei asigurate survine anterior sau vor incasa suma de S₂ u.m. si in situatia in care decesul survine dupa varsta de x + n ani.

Este o asigurare cu suma dubla deoarece, daca asiguratul moare dupa n ani, din asigurare se degaja doua sume: una incasata de asigurat datorita faptului ca a supravietuit varstei de x + n ani, iar cea de-a doua suma o vor primi urmasii in cazul decesului sau, dupa momentul x + n.

Prima neta unica poate avea una dintre urmatoarele forme:

a) daca S1 ≠S2 atunci P_nu= S_1∙ vⁿ ₊ S_2∙nsau P_nu= S_{1∙( )}ⁿ₊ S₂

b) daca S1 = S2 avem P_nu= S_1∙ (vⁿ _{+ n}sau P_nu= S_{1∙( )}ⁿ₊

Astfel, daca o persoana in varsta de 25 de ani incheie o asigurare mixta cu suma dubla prin care urmeaza sa primeasca suma de 500 000 u.m. peste 15 ani daca este in viata ori urmasii acesteia, in cazul in care asiguratul moare, cunoscand valoarea numerelor de comutatie D₄₀= 2013, D₂₅= 8777, M₂₅ =385, putem determina prima neta unica achitata de asigurat: P_nu = 500 000= 136.607,04 u.m.

4.Prima neta anuala sau subanuala la asigurarile de viata

Pentru toate tipurile de asigurari prezentate pana acum am determinat de fiecare data prima neta unica achitata de asigurat la incheierea politei.

Sunt numeroase cazuri in care plata primei nete unice presupune un efort mare din partea asiguratului.

Astfel pentru a elimina acest inconvenient asiguratorii accepta plata fractionata a primelor in concordanta cu principiul echivalentei sarcinilor financiare.

Plata primelor de asigurare se poate efectua anual sau subanual, prin achitarea obligatiilor de catre asigurati lunar, trimestrial sau semestrial in functie de puterea lor financiara.

Determinarea primei nete anuale presupune ca valoarea actuala probabila a tuturor fluxurilor financiare platite de asigurat sa fie egala cu valoarea primei nete unice.

Prima neta anuala depinde de valoarea primei nete unice si de durata perioadei de plata a acestora.

Indiferent de tipul de asigurare, relatia care ne genereaza prima neta anuala (Pna) este urmatoarea:

P_nu= P_na cu plata anticipata a primelor de asigurare si P_nu= P_na cu plata posticipata a primelor de asigurare unde n este durata platii.

In raport cu numerele de comutatie avem urmatoarele expresii pentru prima neta anuala:

P_na=∙ P_nu sau P_na=∙ P_nu

5. Stabilirea primei brute la asigurarile de viata

Prima bruta sau tarifara este formata din prima neta si adaosul de prima.

Prima neta reprezinta suma perceputa de asigurator astfel incat sa acopere riscurile asumate fata de asigurati.

Adaosul de prima cuprinde:

a) cheltuieli de achizitie de contracte (α): cuprind cheltuielile de personal si se efectueaza la incheierea contractului;

b) cheltuieli de incasare de prime (ß): in general, corespund comisionului incasatorului si se exprima in procente din prima neta. Aceste cheltuieli se efectueaza fie dintr-o data, cand asigurarea este cu prima unica sau periodic in timp, cand prima se achita fractionat

c) cheltuielile anuale de administratie g) se exprima in procente din suma anuala;

d) cheltuielile de reglementare a prestatiilor d) se determina prin aplicarea procentului asupra primei nete;

Primele brute se fundamenteaza dupa acelasi principiu al valorii actuale probabile ca si in cazul primelor nete.

Astfel, in conformitate cu acesta valoarea actuala probabila a primelor brute la momentul incheierii contractului de asigurare trebuie sa fie egala cu valoarea actuala probabila a sarcinilor financiare si serviciilor prestate de asigurator.

Echivalenta eforturilor financiare ale asiguratorului si asiguratului se transpun matematic in urmatoarea forma:

P_bruta=P_neta + a+ b ∙ P_bruta+ g×+ d× P_neta

sau P_bruta=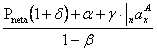

unde coeficientii a b g si d sunt normati iar n reprezinta durata asigurarii.

Daca asigurarea contractata de asigurat se desfasoara pe toata durata vietii, atunci prima bruta se calculeaza dupa urmatoarea formula :

P_bruta=

Prima bruta de asigurare are urmatoarele expresii in functie de tipul de asigurare:

1. Asigurarea de supravietuire cu plata unica

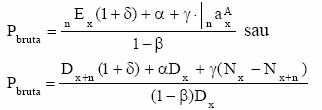
2. Anuitate imediata nelimitata anticipata

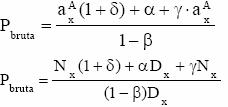
Anuitate imediata limitata anticipata

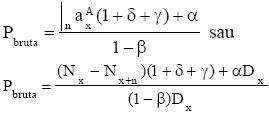
4. Anuitate amanata nelimitata anticipata

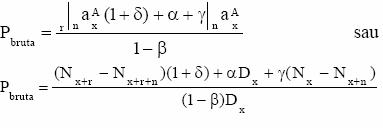
5. Asigurare de deces imediata nelimitata

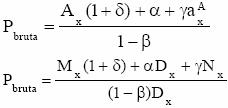
6. Asigurare de deces imediata limitata

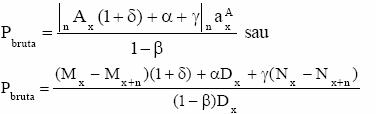
7. Asigurare de deces amanata nelimitata

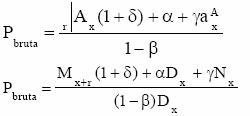
8. Asigurare de deces amanata limitata

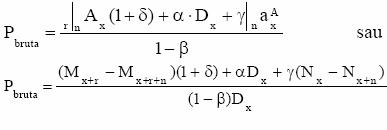
Exemplu:

O persoana in varsta de 30 de ani incheie o asigurare de supravietuire prin care primeste peste 10 ani, daca este in viata suma de 1 000 000 u.m. Societatea de asigurari practica urmatoarele procente :

Æa = 2,3% din suma asigurata;

Æb = 2,7% din prima neta;

Æg = 0,3% din suma asigurata;

Æd = 0,2% din prima neta.

In aceste conditii prima bruta unitara achitata de asigurat va fi :

P_{bruta unitara =}

P_{bruta unitara =}

P_{bruta unitara} = 0,4279436

Prima tarifara totala se obtine prin multiplicarea primei brute unitare cu suma asigurata de 1 000 000 u. m., ceea ce conduce la o prima bruta totala de 427 94

Prima neta pentru aceasta asigurare este de 372 570 u.m. diferenta pana la valoarea primei brute fiind adaosul de prima.

Consider ca societatea de asigurari trebuie sa-si fundamenteze pe baze matematice prima bruta pentru a diminua riscul de neindeplinire a obligatiilor fata de asigurati.

De asemenea, asiguratorii pot utiliza adaosul de prima ca un adevarat instrument de promovare a produselor pe piata.

Daca asiguratul ar fi depus intr-o banca o suma egala cu prima bruta de asigurare atunci el ar beneficia peste 10 ani de o suma cu 109 000 u.m. mai mare decat in cazul asigurarii.

In schimb daca ar plasa suma aferenta primei nete in aceleasi conditii intr-o banca ar obtine cu aproximativ 50 000 u.m. mai putin.

Societatea de asigurari este nevoita sa-si ajusteze corespunzator primele si procentele practicate pentru acoperirea cheltuielilor suplimentare astfel incat produsul sa fie atractiv iar asiguratorul sa poata sa obtina un profit.

6. Probabilitati pentru grupuri de persoane

6.1. Aspecte teoretice

Fie un grup format din n persoane cu varstele de x₁,x₂,x₃,,x_n. Notam cu _tp_x1xn probabilitatea ca tot grupul sa fie in viata peste t ani.

Deoarece se doreste ca peste t ani toate persoanele sa fie in viata, atunci trebuie ca fiecare dintre ele sa fie in viata peste t ani.

Asadar avem:

_tp_x1xn

Inlocuind probabilitatea de viata se obtine:

_tp_x1xn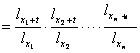

In acelasi mod se poate determina si probabilitatea ca tot grupul sa moara peste t ani. Aceasta se noteaza cu _tq_x1xn si este egala cu produsul tuturor probabilitatilor de deces ale indivizilor grupului respectiv peste t ani.

_tq_x1xn

Daca inlocuim probabilitatile de deces in raport cu functia de supravietuire, relatia de mai sus capata urmatoarea forma:

_tq_x1xn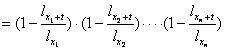

In cadrul asigurarilor de grupuri de persoane un loc aparte il ocupa probabilitatile de tipul : tot grupul sa fie in viata, cel putin un anumit numar de persoane sa fie in viata sau numai un numar de persoane sa fie in viata.

Pentru exemplificare se considera un grup format din trei persoane cu varstele de x₁, x₂, x₃ si sa calculam:

a.probabilitatea ca tot grupul sa fie in viata dupa un numar de t ani;

b.probabilitatea ca numai o persoana sa fie in viata dupa un numar de t ani;

c.probabilitatea ca numai doua persoana sa fie in viata dupa un numar de t ani;

d.probabilitatea ca cel putin o persoana sa fie in viata dupa un numar de t ani;

e.probabilitatea ca cel putin doua persoana sa fie in viata dupa un numar de t ani;

f.probabilitatea ca tot grupul sa moara dupa un numar de t ani.

a.pentru ca tot grupul sa fie in viata dupa un numar de t ani trebuie ca fiecare individ sa fie in viata la momentul respectiv.

_tp_x1x2x3= _tp_{x1∙ t}p_{x2∙ t}p_x3

_tp_x1x2x3=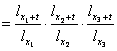

b. deoarece numai o singura persoana trebuie sa fie in viata peste t ani, atunci avem urmatoarele posibilitati: prima sa fie in viata si celelalte doua sa moara sau a doua sa fie in viata si prima si a treia sa moara sau primele doua sa moara si a treia sa traiasca. Deci:

p= _tp_{x1∙ t}q_{x2∙ t}q_{x3+ t}q_{x1∙ t}p_{x2∙ t}q_{x3+ t}q_{x1∙ t}q_{x2∙ t}p_x3

Exprimata in raport cu functia de supravietuire aceasta probabilitate are urmatoarea forma:

p₊₊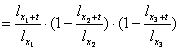

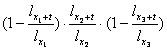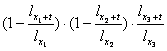
c.In cazul in care numai doua persoane sunt in viata peste t ani exista, de asemenea trei posibilitati, cate doua in viata, iar cea de-a treia moare:

p= _tp_{x1∙ t}p_{x2∙ t}q_{x3+ t}p_{x1∙ t}q_{x2∙ t}p_{x3+ t}q_{x1∙ t}p_{x2∙ t}p_x3

Inlocuind probabilitatile de viata avem:

p₊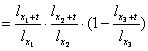

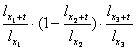
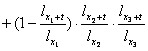
d.probabilitatea ca cel putin o persoana sa fie in viata presupune existenta urmatoarelor variante posibile: numai o persoana sa fie in viata sau numai doua persoane sa fie in viata, ori tot grupul sa supravietuiasca peste t ani.

Deci p = probabilitatea ca numai o persoana sa fie in viata peste t ani + probabilitatea ca numai doua persoane sa fie in viata peste t ani + probabilitatea ca tot grupul sa supravietuiasca peste t ani.

Scriind desfasurat probabilitatea ca macar o persoana sa traiasca peste t ani este:

p = _tp_{x1∙ t}q_{x2∙ t}q_{x3+ t}q_{x1∙ t}p_{x2∙ t}q_{x3+ t}q_{x1∙ t}q_{x2∙ t}p_{x3 + t}p_{x1∙ t}p_{x2∙ t}q_{x3+ t}p_{x1∙ t}q_{x2∙ t}p_{x3+ t}q_{x1∙ t}p_{x2∙ t}p_{x3 + t}p_{x1∙ t}p_{x2∙ t}p_x3

e.In cazul in care cel putin doua persoane sunt in viata avem urmatoarele posibilitati: numai doua persoane in viata sau toate trei sa fie in viata peste t ani.

Deci p = probabilitatea ca numai doua persoane sa fie in viata peste t ani + probabilitatea ca tot grupul sa supravietuiasca peste t ani.

p = _tp_{x1∙ t}p_{x2∙ t}q_{x3+ t}p_{x1∙ t}q_{x2∙ t}p_{x3+ t}q_{x1∙ t}p_{x2∙ t}p_{x3 + t}p_{x1∙ t}p_{x2∙ t}p_x3

f.Daca tot grupul moare peste t ani, probabilitatea este egala cu:

_tq_x1x2x3= _tq_{x1∙ t}q_{x2∙ t}q_x3

_tq_x1x2x3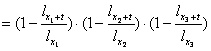

6.2.Polinomul lui Poisson

Probabilitatile de supravietuire pentru grupuri de persoane de tipul numai se pot determina si cu ajutorul acestui polinom.

Se considera urmatorul polinom:

P(x)=(_tp_x1X+_tq_x1) ∙(_tp_x2 X +_tq_x2) ∙(_tp_x3 X +_tq_x3)

Coeficientul lui x³ reprezinta probabilitatea ca tot grupul sa fie in viata peste t ani;

Coeficientul lui x² reprezinta probabilitatea ca numai doua persoane sa fie in viata peste t ani;

Coeficientul lui x¹ reprezinta probabilitatea ca numai o persoana sa fie in viata peste t ani;

Coeficientul lui x⁰ (termenul liber) reprezinta probabilitatea ca tot grupul sa moara peste t ani.

Daca desfacem parantezele, polinomul are urmatoarea forma:

P(x)=(_tp_x1∙tp_x2∙x²+_tp_x1∙tq_x2∙x_+tq_x1∙tp_x2∙x+ _tq_x1∙tq_x2)( _tp_x3∙x+ _tq_x3) = _tp_x1∙tp_{x2∙ t}p_x3∙x³+ _tp_x1∙tp_{x2∙ t}q_x3∙x²+ _tp_x1∙tq_{x2∙ t}p_x3∙x²+ _tp_x1∙tq_{x2∙ t}q_x3∙x ₊ +_tq_x1∙tp_{x2∙ t}p_x3∙x² _+tq_x1∙tp_{x2∙ t}q_x3∙x+ _tq_x1∙tq_{x2∙ t}p_x3∙x+ _tq_x1∙tq_{x2 ∙t}q_{x3 =}

= _tp_x1∙tp_{x2∙ t}p_x3∙x³+x²(_tp_x1∙tp_{x2∙ t}q_x3+ _tp_x1∙tq_{x2∙ t}p_x3+ _tq_x1∙tp_{x2∙ t}p_x3)+x(_tq_x1∙tp_{x2∙ t}q_x3+ _tq_x1∙tq_{x2∙ t}p_x3+ _tp_x1∙tq_{x2∙ t}q_x3)+ _tq_x1∙tq_{x2 ∙t}q_x3

Se observa ca am obtinut aceleasi rezultate ca in problema precedenta.

6.Aplicatii practice

1. Se da un grup format din doua persoane cu probabilitatile de supravietuire peste n ani p₁ si p₂. Probalilitatea ca numai o persoana sa fie in viata peste n ani este:

a. p₁-p₂+p₁p₂;

b.p₁-p₂-p₁p₂;

c.p₁+p₂-2p₁p₂.

Rezolvare:

Probabilitatea ca numai o persoana sa fie in viata dintr-un grup de doua persoane este urmatoarea :

P = _np_x1∙nq_x2+ _nq_x1∙np_x2

adica una dintre ele trebuie sa moara si una trebuie sa traiasca.

Dar _np_x1=p₁;  _np_x2=p₂; _nq_x1= 1- p₁; _nq_x2= 1- p_2.

Inlocuind in prima relatie obtinem

P = p₁(1- p₂)+( 1- p₁) p₂ = p₁+p₂-2p₁p₂, deci raspunsul corect este c.

2. Fie un grup format din patru persoane cu varstele x₁,x₂, x₃, si x₄.

Calculati:

a.probabilitatea ca macar trei persoane sa fie in viata peste t ani;

b.probabilitatea ca numai doua persoane sa fie in viata peste t ani;

Rezolvare:

a. p = _tp_{x1∙ t}p_{x2∙ t}p_{x3∙ t}q_x4+ _tp_{x1∙ t}p_{x2∙ t}q_{x3∙ t}p_x4+ _tp_{x1∙ t}q_{x2∙ t}p_{x3∙ t}p_x4+ _tq_{x1∙ t}p_{x2∙ t}p_{x3∙ t}p_x4+ _tp_{x1∙ t}p_{x2∙ t}p_{x3∙ t}p_x4

b. p = _tp_{x1∙ t}p_{x2∙ t}q_{x3∙ t}q_x4+ _tp_{x1∙ t}q_{x2∙ t}p_{x3∙ t}q_x4+ _tp_{x1∙ t}q_{x2∙ t}q_{x3∙ t}p_x4+ _tq_{x1∙ t}q_{x2∙ t}p_{x3∙ t}p_x4+ _tq_{x1∙ t}p_{x2∙ t}q_{x3∙ t}p_x4+ _tq_{x1∙ t}p_{x2∙ t}p_{x3∙ t}q_x4

Fie un grup format din doua persoane cu varstele de 36 si 42 de ani. Cunoscand valorile functiei de supravietuire l₄₄=88.883, l₃₆ = 92.743, l₅₀ =84.108, l₄₂ = 90.063, precizati care dintre formulele de mai jos reprezinta polinomul lui Poisson asociat grupului respectiv:

a. 0,102238x²+0,895010 x+0,002752;

b. 0,895010 x² +0,102238x +0,002752;

c. 0,002752x²+0,895010 x+0,102238.

Din valorile date pentru functia de supravietuire tragem concluzia ca este vorba de gasirea polinomului pentru perioada de 8 ani. (x1=36, x2=42, n = 8 ani).

Polinomul lui Poisson pentru un grup de doua persoane este:

p(x)= (p₁x+q₁) (p₂x+q₂)

Tinand cont ca q₁ =1-p₁ si q₂ =1-p₂ obtinem :

p(x)= (p₁x+1-p₁) (p₂x+1-p₂) = p₁p₂x² + (p₁+p₂-2p₁p₂)x+ +1+p₁p₂-p₁-p₂

Avand valorile pentru functia de supravietuire putem calcula probabilitatile de viata ale persoanelor respective peste 8 ani.

p₁ =₈p₃₆=== 0, 958379

p₂ =₈p₄₂=== 0,933879

Atunci:

p₁p₂ = 0, 958379 ∙0,933879= 0,895010

p₁₊p₂- 2 p₁p₂ = 0,102238

1+ p₁p₂- p₁-p₂= 0,002752

Deci polinomul lui Poisson cerut este

0,895010 x² +0,102238x +0,002752, deci raspunsul corect este b.

7. Asigurari de supravietuire pentru grupuri de persoane

Aspecte teoretice

Un grup format din n persoane incheie o asigurare prin care urmeaza sa primeasca suma S daca:

Tot grupul - este in viata peste t ani;

Numai k persoane - sunt in viata peste t ani;

Cel putin k persoane - sunt in viata peste t ani.

Sa se calculeze prima neta unica pe care trebuie sa o plateasca grupul respectiv societatii de asigurari.

In acest caz prima neta unica va fi

P_nu =S∙v^t∙p

Unde, S = suma asigurata;

i = rata de dobinda;

v = - factor de actualizare;

t - durata asigurarii;

p - probabilitatea ca:

Tot grupul - este in viata peste t ani;

Numai k persoane - sunt in viata peste t ani;

Cel putin k persoane - sunt in viata peste t ani.

7.2.Aplicatii practice

1. Un grup format din trei persoane in varsta de 30, 40 si 42 de ani incheie o asigurare prin care urmeaza sa primeasca peste 18 ani suma de 180.000 u.m daca doar doua persoane sunt in viata. Stiind ca polinomul lui Poisson pentru grupul respectiv este P(x)=0,9346x³+0,9497x²+0,8723x+0,5436, iar procentul anual utilizat este de 16%, sa se determine prima neta unica.

Rezolvare:

Prima neta unica in acest caz va fi:

P_nu =S∙vⁿ∙p

unde: S =180.000 u.m.;

v = =;

n = 18 ani;

p - probabilitatea ca numai doua persoane sa fie in viata este data de coeficientul lui x² din polinomul lui Poisson, deci p = 0,9497.

Pnu = 180.000∙∙0,9497=11.819,93633

2. Asigurarea de supravietuire pe 12 ani pentru un grup format din trei persoane cu varstele de 23, 32 si 28 de ani prevede ca societatea sa plateasca suma de 420.00 u.m, la scadenta, daca cel putin o persoana este in viata. Cunoscand procentul anual de dobanda de 10% si valorile functiei de supravietuire l₂₃ =95.378, l₃₂ = 9875, l₂₈ = 94.643, l₃₅ = 9067, l₄₄ = 88.883, l₄₀ = 91.128, sa se determine prima neta unica datorata de asigurat.

Rezolvare:

Stim ca: x₁ = 23, x₂ = 32, x₃ = 28, , n = 12, i = 10%, S = 420.000 u.m.

Prima neta unica aferenta asigurarii este P_nu = S∙vⁿ∙p, unde p este probabilitatea ca cel putin o persoana dintr-un grup de trei persoane sa fie in viata.

P = _np_{x1∙ n}p_{2∙ n}p_{x3+ n}p_{x1∙ n}p_{x2∙ n}q_{x3+ n}p_{x1∙ n}q_{x2∙ n}p_{x3+ n}q_{x1∙ n}p_{2∙ n}p_{x3+ n}p_{x1∙ n}q_{2∙ n}q_{x3+ n}q_{x1∙ n}p_{2∙ n}q_{x3+ n}q_{x1∙ n}q_{2∙ n}p_x

p = ₁₂p_{23∙ 12}p_{32∙ 12}p_{28+ 12}p_{23∙ 12}p_{32∙ 12}q_{28+ 12}p_{23∙ 12}q_{32∙ 12}p_{28+ 12}q_{23∙ 12}p_{32∙ 12}p_{28+ 12}p_{23∙ 12}q_{32∙ 12}q_{28+ 12}q_{23∙ 12}p_{32∙ 12}q_{28+ 12}q_{23∙ 12}q_{32∙ 12}p_28.

P=+++++

++= 0,999949

P_nu=420.000∙∙0,999949 = 13818,1184

O familie formata din doua persoane cu varstele de 30 si 29 de ani incheie o asigurare prin care urmeaza suma de 750.000 u.m. peste 10 ani daca numai o persoana este in viata. Utilizand procentul anual de dobanda de 10% si valorile functiei de supravietuire l₃₀ =94.284, l₂₉ = 94.475, l₄₀ = 91.128, l₃₉ = 91.585, sa se determine prima neta unica aferenta asigurarii.

Rezolvare:

Prima neta unica pe care trebuie sa o achite asiguratul este P_nu = S∙vⁿ∙p, unde p este probabilitatea ca numai o persoana sa fie in viata dintr-un grup de doua persoane.

P = _np_x1∙_nq_x2+ _nq_x1∙_np_x2

dar x₁=30, x₂ = 29, n = 10, i = 0,1 si S = 750.000 u.m.

p = +

p = +

Inlocuind valorile functiei de supravietuire se obtine p = 0,062015

P_nu = 750.0000,062015

P_nu = 17.932,10032

Autoevaluare:

1.Care sunt principalele tipuri de asigurari de supravietuire pe care le cunoasteti?

Care sunt principalele tipuri de asigurari mixte de viata cunoscute in practica asigurarilor?

De ce depinde valoarea primei nete anuale in cazul asiguraprilor de viata ?

Rezumatul acestei sectiuni:

La baza stabilirii primelor in cazul asigurarilor de viata stau urmatoarele principii:

º principiul echivalentei sarcinilor;

º principiul aditivitatii primelor.

Referate propuse

Referatul numarul 1: Asigurarea mixta cu suma dubla

Referatul numarul 2:Asigurarea mixta cu termen fix

Referatul numarul 3:Asigurarea de supravietuire imediata nelimitata;

Probleme propuse spre rezolvare:

Problema numarul 1:

O persoana in varsta de 27 de ani incheie o asigurare de supravietuire cu plata fractionata imediata nelimitata prin care urmeaza sa primeasca pe toata durata vietii la inceputul fiecarei luni suma de 700 000 u.m.

Se cere sa se determine prima neta unica datorata de asigurat in acest caz (i = 10%).

Problema numarul 2:

O persoana in varsta de 38 de ani incheie o asigurare de supravietuire cu plata anuala imediata limitata prin care urmeaza sa primeasca pana la implinirea varstei de 53 de ani la sfarsitul fiecarui an suma de 700 000 u.m.

Se cere sa se determine prima neta unica datorata de asigurat in acest caz (i = 10%).

Bibliografie:

1.Alexandru Felicia, Armeanu Daniel, - "Asigurari de bunuri si persoane: aspecte teoretice, aplicatii practice", Editura Economica, Bucuresti, 2003

2.Begam Gabriela, "Metode probabilistice aplicate in economie si asigurari", Editura Tehnica, Bucuresti, 1996

Bente Corneliu,- "Fundamentarea tarifelor de prime la asigurarile de bunuri", Revista Finante-Banci-Asigurari, Nr. 7/2006

4.Purcaru Ion, Mircea Iulian, Lazar Gheorghe, - "Asigurari de persoane si de bunuri", Editura Economica, Bucuresti, 1998

5.Purcaru Ion, - "Matematica si asigurari", Editura Economica, Bucuresti, 1994