GEOMETRIA SI CINEMATICA DEFORMATIEI SI MISCARII

GEOMETRIA SI CINEMATICA DEFORMATIEI SI MISCARII

1 GEOMETRIA DEFORMATIEI

Deformatia mediului continuu la un moment t este caracterizata de variatia configuratiei sale geometrice D din acel moment in raport cu configuratia geometrica a aceluiasi mediu dintr-un moment considerat ca referinta. Drept referinta se poate lua configuratia initiala D⁰ din momentul t⁰ sau orice alta configuratie dintr-un moment anterior momentului t.

1.1 TENSORII STARII DE DEF ORMATIE

1.1.1 Tensorii gradientului deformatiei si gradientul deplasarii

Se considera intr-un punct P⁰ din configuraiia initiala D⁰ un vector infinitesimal dx⁰ pe o curba materiala oarecare. Imaginea dx in configuratia actuala D a elementului dx⁰ se obtine din relatia evidenta , unde .Ea se scrie sub forma

Unde (v. nota de subsol de la A172) si (A99) cu F s-a notat tensorul de ordinul al doilea

Desi tensorul F care realizeaza transformarea vectorului dx0 in dx caracterizeaza in mod sigur cinematica miscarii mediului, el putand caracteriza si deformatia acestuia, el se numeste totusi tensorul gradientului deformatiei. Tensorul F este definit pe D⁰ si are matricea asociata

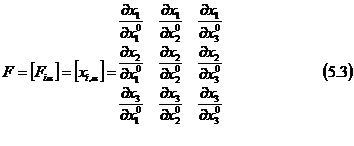
Al carei determinat este jacobianul transformarii (v.4.7) diferit de zero,

Scriind  vectorul x sub forma , se obtine

Din (1) si (5), rezulta relatia

Unde I este tensorul unitate iar F_u tensorul gradientul deplasarii in raport cu coordonatele materiale. Tensorul F_u este definit pe D⁰ si are matricea asociata

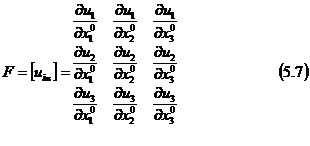
Daca se utilizeaza coordinate euleriene, din (2) sau (4.8) se obtine

Unde,

Tensorul H este definit pe D. El are matricea asociata Se observa ca H exista, intrucat Tensorul H se poate exprima si prin gradientul deplasarii in raport cu coordonatele spatiale. Din relatia (4.12)₁, se obtine

(10)

De unde, tinand seama si de (8), rezulta

(11)

Descompunerea polara tensorului gradientului deformatiei

Tensorul nesingular gradientul deformatiei se poate descompune polar in mod unic sub forma (v.(A124)),

(12)

Unde U si V sunt tensorii simetrici pozitiv definiti, avand acelasi valori proprii Si aceiasi vectori proprii si iar R este o transformare ortogonala proprie, Inlocuind (12) in (1), rezulta,

Considerand aceasta relatie ca o succesiune de doua transformari (v.A1.82) asupra vectorului dx⁰, se poate spune ca deformatia locala se obtine fie aplicand vectorul dx⁰ transformarea U si apoi rotatia R vectorului fie aplicand mai intai rotatia R vectorul dx⁰ si apoi transformarea V vectorului Deformatia propriuzisa a mediului este caracterizata de tensorul U, deoarece daca U ar fi I ar rezulta , adica o rotatie de rigid a elementului (v.A52). Din acest motiv R se mai numeste tensor de rotatie sau tensor orthogonal propriu Dimpotriva, pentru , s-ar obtine . Daca rezulta 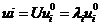.Aplicand rotatia R, se obtine Se deduce ca valorile proprii reprezinta raportul dintre lungimea imaginii prin F a vectorului propriu si lungimea acestui vector in D⁰, de aceea se numesc alungiri principale iar tensorul U se numeste tensor de alungire la dreapta (intai s-a efectuat deformarea si apoi rotatia-transformarea RU.) Daca se foloseste tensorul V, se obtine relatia , care arata ca tensorul V are tot valorile proprii , vectorii proprii fiind Rezulta ca are loc intai rotatia vectorilor proprii, obtinandu-se si apoi deformarea acestora in rapoartele . Tensorul V se numeste tensor alungire la stanga.

1.1.2 Tensorii Cauchy-Green

Tensorul deformatie la Cauchy-Green dreapta

Tensorul F se numeste impropriu tensorul gradientului deformatiei, intrucat el poate exista chiar daca deformatiile propiu-zise sunt nule cum se intampla, de exemplu, in miscarea de rotasie a rigidului.

Deformatia propriu-zisa a mediului in vecinatatea unui punct P din D este caracterizata in mod sigur de variatia produsului scalar dintre doi vectori infinitezimali concurenti in P⁰ (P este imaginea in D a punctului P⁰ din D⁰)

(13)

Prin trecerea de la configuratia de referinta la configurasia actuala, vectorii infinitezimali devin Pe baza definitiei prodausului scalar, rezulta ca aceasta ramane invariant numai atunci cand mediului nu se deformeaza-putand avea insa miscare de rigid. Tinand seama de (1), se obtine (v. si A110)

(14,a)

Tensorul simetric

(15)

Definit pe D⁰, se numeste tensorul deformatiei Cauchy-Green la dreapta. El are coordonatele

(16)

Astfel incat produsul scalar (14, a) devine

(14,b)

Sau metrical (v. si (A2.93), (A2.53, c), )A2.92),

(17)

Unde C este matricea asociata tensorului C,

(18)

Observatie. Produsul scalar (14, a) se mai poate scrie sub forma

(19)

unde sunt coordonatele tensorului ce defineste metrica in configuratia deformata (v.(A191)₁). Fiind exprimata printr-un produs scalar, metrica este euclidiana (v.p.A1.2.3). Din (14, b) si (19), rezulta

(20)

Tinand seama de (6), tensorul C se poate exprima si in functie de tensorul gradientului deplasarii in raport cu coordonatele materiale,

(21)

In coordonate, , adica

(22)

Din (13) si (14) rezulta ca, variatia produsului scalar prin trecerea de la configuratia de referinta la configuratia actuala-variatie exprimata in functie de tensorul deformatie Cauchy-Green la dreapta-are expresia

(23)

Observatie. Intre tensorul deformatie Cauchy-Green la dreapta si tensorul alungire la dreapta (12)₁ se stabileste cu usurinta relatia

(24)

Semnificatia coordonatelor tensorului Cauchy-Green la dreapta

a)     Variatia relativa a lungimii elementelor paralele cu axele

Fie in configuratia initiala D⁰ un element dispus pe o linie materiala cu directia si avand lungimea Daca, de exemplu, se considera elemental paralel cu axa se poate scrie .Din definitia produsului scalar, rezulta patratul lungimii elementului

Patratul lungimii aceluiasi elemnt, dar in configuratia D, este dat de de relatia

Efectuand produsul scalar conform (17), se obtine

In general se poate scrie

fara sumare (25)

Alungirea relativa a elementului paralel cu axa este

fara sumare (26)

b)     Variatia unghiurilor drepte dintre elementele paralele cu axele

Se considera in configuratia initiala D⁰ doua elemente , paralele respective cu axele de coordonate si avand marimile respective evident, produsul lor scalar este nul . In configuratia actuala, elementele si devin respective, avand marimile respectiv Produsul scalar al vectorilor si se scrie geometric sub forma unde este variatia unghiului dintre vectorii si (egal initial cu 90°) El se numeste unghi de lunecare specifica in planul si se va nota cu

Se determina marimile care intervin in (27). Se considera elemental …. Parallel ………. Tinind seama de (17), se poate scrie ………………Produsul …….. se calculeaza cu relatia (25)…….. rezulta ……………….

c)      Variatia elementului de volum

In procesul de deformare, volumul ,,,,,,,,,, al domeniului ……….. se modifica. Orice volum elementar ……. Devine ………………. (v.(A210)).Tind seama de (4) si (18), rezulta

Adica

Variatia volumului elementar la trecerea din configuratia ……….. in configuratia ………… este ……………, iar variatia relativa a volumului elementar este

De unde rezulta

d)     Variatia elementului de arie

Fie o arie orientata …… in configuratia ………….., definita de doi vectori elementary, …………………., necoliniari, dispusi pe linii materiale si concurenti in punctual ………….(in particular ei pot fi paraleli cu ………………). Conform (A7), se scrie…………. Imaginea in D a vectorului ………………. Este ………………. Se considera in ………… un al treilea vector ……. Necoplanr cu …………………… Imaginea vectorului ……………….. in D este …………….Volumul paralelipipedului construit pe vectorii …………… ca laturi (v.(A10)) este ………… , iar volumul paralelipipedului avand ca laturi vectorii ………………….Rezulta

Sau

Tensorul deformatiei Cauchy-Green la stanga

Variatia produsului scalar a doi vectori infinitezimali ………….. concurenti intr-un punct …………… din …………. Se poate exprima si in functie de coordinate euleriene. Tinand seama de (8), se scrie

Unde cu B s-a notat tensorul deformatiei Cauchy-Green la stanga (v.si (9)).

Tensorul ……………. Care intervine in expresia produsului scalar (33) are coordonatele

Rezulta urmatoare expresie pentru variatia produsului scalar,

Tensorul ………. Se poate exprima si cu ajutorul tensorului gradient al functiei deplasare exprimata prin coordonatele spatiale. Tinand seama de (11), se obtine relatia

Sau, in coordonate,

Observatie. Intre tensorii B si V (12)₂ se stabileste cu usurinta relatia