Legea conservarii energiei mecanice
Plecand de la definitia
lucrului mecanic s-a demonstrat teorema energiei cinetice pentru un punct
material: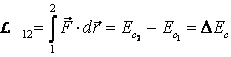 
. Sa deducem aceasta teorema analitic.
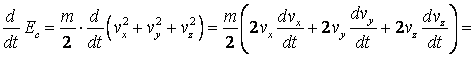
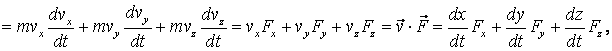de unde rezulta in cazul unei forte care nu variaza in
timp,
,
(2.32)
unde 
este lucrul mecanic
elementar. Integrand intre st area initiala (1) si finala (2) obtinem:
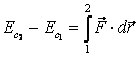(2.33)
In unele cazuri
particulare de forte integrala din (2.33) nu depinde de drum, astfel ca poate
fi scrisa ca diferenta dintre valorile unei marimi ce depinde numai de
coordonate, numita energie potentiala
a corpului, in cele doua stari (1, respectiv 2). In acest caz forta 
se numeste forta conservativa, deoarece sub
actiunea acestei forte energia mecanica a corpului se conserva in timp.
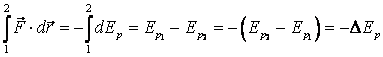. (2.34)
Comparand (2.33) si (2.34) se obtine:
,
adica
Forma diferentiala a relatiei (2.34):
(2.35)
se mai numeste si diferentiala totala exacta.
Expresia (2.35) se mai poate scrie si astfel:
,
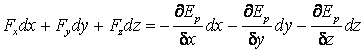de unde rezulta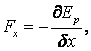 
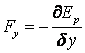si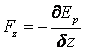 
, sau echivalent:
. (2.36)
Prin gradientul unei functii scalare de coordonate intelegem operatorul diferential "nabla", care este un vector:
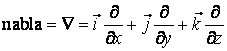(2.37)
aplicat functiei respective, in cazul nostru 
:
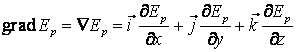(2.38)
Daca pentru oricare pereche de doua componente ale fortei facem operatiile urmatoare:
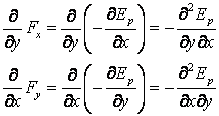
se obtine, in conditiile teoremei lui Schwartz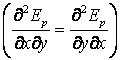 
egalitatea:
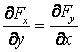, (2.39)
de unde, prin permutari circulare obtinem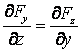 
, respectiv 
.
Definind operatorul diferential "rotor"
aplicat unui vector 
prin relatia
(2.40)
si aplicand acest
operator vectorului 
, obtinem:
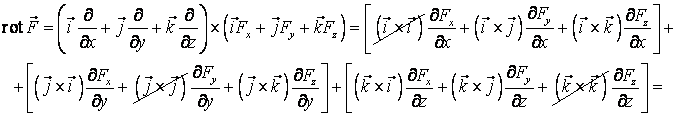
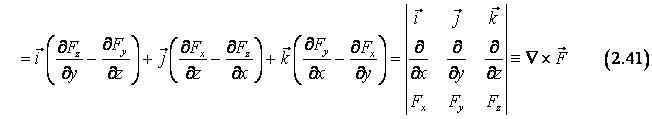unde s-a tinut cont de relatiile dintre versorii 
, 
si 
: 
si 
Astfel, tinand cont de identitatile (2.39) se obtine
(2.42)
care este o conditie necesara si suficienta ca forta sa fie conservativa.
Din relatia 
rezulta ca 
este definita pana la
o constanta ce este determinata din conditia
ca sa aiba valoarea aleasa intr-un punct.
Sumand relatiile de tipul
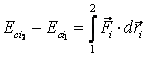(2.43)
pentru toate punctele materiale ale unui sistem, obtinem:
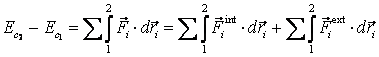, (2.44)
unde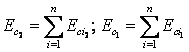 
. Aceste integrale depind, in cazul general, de traiectoriile
tuturor punctelor sistemului.
In cazul fortelor interioare de tip conservativ, integralele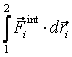 
nu depind de drum, si
putem scrie, sub forma diferentiala sau integrala:
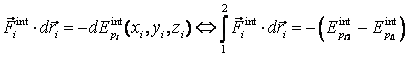(2.45)
Sumand pe toate particulele sistemului obtinem:
(2.46)
fiind energia
potentiala a intregului sistem datorata fortelor interioare, iar
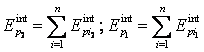
Din (2.44) obtinem:
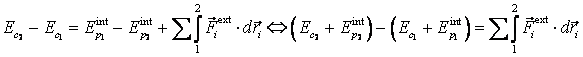, (2.47)
formula valabila in cazul general cand asupra sistemului actioneaza forte exterioare neconservative.
Daca sistemul nu sufera actiuni din exterior si toate fortele interioare sunt conservative, atunci:
,
sau, renuntand in acest caz la indicele "int":
, (2.48)
adica legea
conservarii energiei mecanice pentru sistemul de 
puncte materiale.
https://www.qtransform.com/ - transforma unitatile de masura.
