|
Miscarea oscilatorie
 Sub actiunea unei forte elastice un
punct material de masa
Sub actiunea unei forte elastice un
punct material de masa ![]() executa o miscare
oscilatorie armonica. Un exemple simplu este deformarea unui arc (resort). Sa
deducem ecuatia de miscare a unui corp punctiform de masa
executa o miscare
oscilatorie armonica. Un exemple simplu este deformarea unui arc (resort). Sa
deducem ecuatia de miscare a unui corp punctiform de masa ![]() sb actiunea fortei
elastice
sb actiunea fortei
elastice ![]() . In fig.2
. In fig.2 ![]() in cazul resortului
netensionat, cand forta elastica este zero. Corpul fiind scos din pozitia de echilibru si
lasat apoi liber, asupra lui va actiona forta elastica datorata alungirii sau
comprimarii resortului. Dependenta de timp a pozitiei corpului
in cazul resortului
netensionat, cand forta elastica este zero. Corpul fiind scos din pozitia de echilibru si
lasat apoi liber, asupra lui va actiona forta elastica datorata alungirii sau
comprimarii resortului. Dependenta de timp a pozitiei corpului ![]() se obtine aplicand
legea a doua a lui Newton:
se obtine aplicand
legea a doua a lui Newton:
![]() ;
; ![]()
![]() ,
,
de unde obtinem ecuatia diferentiala de miscare a oscilatorului armonic liniar:
![]() . (2.49)
. (2.49)
Ecuatia:
![]() (2.50)
(2.50)
este o ecuatie diferentiala omogena cu coeficienti constanti, cu solutia generala:
![]() , (2.51)
, (2.51)
unde ![]() si
si ![]() sunt doua constante
care se determina din conditiile initiale, iar
sunt doua constante
care se determina din conditiile initiale, iar ![]() si
si ![]() radacinile ecuatiei
caracteristice:
radacinile ecuatiei
caracteristice:
![]() (2.52)
(2.52)
Ecuatia (2.52) s-a obtinut prin introducerea solutiei (2.51) in ecuatia (2.50).
Ecuatia caracteristica a oscilatorului armonic liniar (2.49), este:
![]() , (2.53)
, (2.53)
cu solutiile:
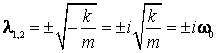 , (2.54)
, (2.54)
unde am folosit notatia 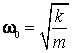 . Marimea
. Marimea ![]() se numeste pulsatia proprie a oscilatorului armonic
liniar. Aceasta depinde de
se numeste pulsatia proprie a oscilatorului armonic
liniar. Aceasta depinde de ![]() a corpului, constituind
o caracteristica fundamentala a oscilatorului elastic. Sensul acestei pulsatii
este urmatorul: daca oscilatorul armonic liniar este scos din pozitia de
echilibru si lasat liber, acesta poate oscila numai cu pulsatia lui proprie
a corpului, constituind
o caracteristica fundamentala a oscilatorului elastic. Sensul acestei pulsatii
este urmatorul: daca oscilatorul armonic liniar este scos din pozitia de
echilibru si lasat liber, acesta poate oscila numai cu pulsatia lui proprie ![]() . In absenta frecarilor, pentru ca un oscilator armonic sa
oscileze cu o pulsatie
. In absenta frecarilor, pentru ca un oscilator armonic sa
oscileze cu o pulsatie ![]() este necesar ca, pe
langa forta elastica a arcului, asupra oscilatorului sa mai actioneze o forta
exterioara periodica de pulsatie
este necesar ca, pe
langa forta elastica a arcului, asupra oscilatorului sa mai actioneze o forta
exterioara periodica de pulsatie ![]() . Din punct de vedere dimensional pulsatia se masoara in
unitatea
. Din punct de vedere dimensional pulsatia se masoara in
unitatea ![]() :
:
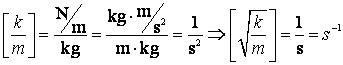
Folosind
solutia (2.54), unde ![]() , ecuatia (2.51) se va scrie:
, ecuatia (2.51) se va scrie:
![]() (2.55)
(2.55)
Deoarece elongatia ![]() reprezinta o marime cu
sens fizic (deplasarea fata de pozitia de echilibru), ea trebuie sa fie
exprimata printr-un numar real. Acest lucru nu se poate realiza decat in conditiile
in care constante le
reprezinta o marime cu
sens fizic (deplasarea fata de pozitia de echilibru), ea trebuie sa fie
exprimata printr-un numar real. Acest lucru nu se poate realiza decat in conditiile
in care constante le ![]() si
si ![]() sunt marimi
complexe. Astfel, vom alege pentru cele doua constante forma analitica:
sunt marimi
complexe. Astfel, vom alege pentru cele doua constante forma analitica:
![]()
![]() (2.56)
(2.56)
In aceste conditii, expresia (2.55) devine:
![]()
Utilizand relatiile lui Euler:
![]()
![]()
ecuatia de miscare a unui oscilator armonic liniar va avea forma:
![]() (2.58)
(2.58)
Din
(2.56) putem determina marimile ![]() si
si ![]() functie de
functie de ![]() si
si ![]()
Fiind solutia unei ecuatii diferentiale de gradul
doi, (2.58) trebuie sa contina doua constante ce sunt determinate de pozitia
initiala ![]() si de viteza
initiala
si de viteza
initiala ![]()
![]() (2.59)
(2.59)
Cu conditiile initiale![]() si
si ![]() rezolvand sistemul
acestor doua ecuatii determinam expresiile lui
rezolvand sistemul
acestor doua ecuatii determinam expresiile lui ![]() si
si ![]()
 (2.60)
(2.60)
Se observa unele diferente esentiale intre
marimile ![]() si
si ![]() pe de o parte, si
pe de o parte, si ![]() pe de alta parte. In
timp ce
pe de alta parte. In
timp ce ![]() este o marime
intrinseca ce caracterizeaza oscilatorul, depinzand de constanta elastica a
resortului si de masa acestuia,
este o marime
intrinseca ce caracterizeaza oscilatorul, depinzand de constanta elastica a
resortului si de masa acestuia, ![]() si
si ![]() pot lua valori
diferite pentru acelasi oscilator, in functie de conditiile initiale.
pot lua valori
diferite pentru acelasi oscilator, in functie de conditiile initiale.
Semnificatia termenilor din relatia (2.58) este urmatoarea:
![]() reprezinta
elongatia miscarii oscilatorii, reprezentand deplasarea oscilatorului fata de
pozitia de echilibru la un moment de timp
reprezinta
elongatia miscarii oscilatorii, reprezentand deplasarea oscilatorului fata de
pozitia de echilibru la un moment de timp ![]()
![]() reprezinta
amplitudinea miscarii oscilatorii, fiind distanta maxima a oscilatorului fata
de pozitia sa de echilibru;
reprezinta
amplitudinea miscarii oscilatorii, fiind distanta maxima a oscilatorului fata
de pozitia sa de echilibru;
![]() reprezinta faza
miscarii oscilatorii, unde
reprezinta faza
miscarii oscilatorii, unde ![]() este faza
initiala;
este faza
initiala;
Se
observa ca functia ![]() din (2.58) este
periodica in timp. Perioada
din (2.58) este
periodica in timp. Perioada ![]() a miscarii poate
fi dedusa din conditia
a miscarii poate
fi dedusa din conditia ![]() , de unde se obtine:
, de unde se obtine:
![]()
iar rezulta expresia perioadei este
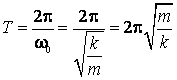 (2.61)
(2.61)
Eliminand timpul intre (2.58) si (2.59) deducem relatia dintre viteza si elongatie:
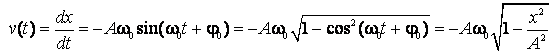 ,
,
de unde rezulta
![]() . (2.62)
. (2.62)
Referitor
la semnul vitezei putem spune ca in general acesta poate fi "+" sau "-",
deoarece la o miscare oscilatorie armonica exista, pentru o elongatie data,
doua pozitii ale corpului in care viteza are aceeasi valoare, dar sensuri opuse
(fig.3, punctele ![]() si
si ![]() ). Din (2.62) se poate observa de asemenea ca pentru
elongatia maxima
). Din (2.62) se poate observa de asemenea ca pentru
elongatia maxima ![]() se obtine
se obtine ![]() , iar pentru elongatia zero viteza este maxima:
, iar pentru elongatia zero viteza este maxima:
![]() (2.63)
(2.63)
Acceleratia miscarii oscilatorii armonice liniare se obtine prin derivarea vitezei:
![]()
Relatia ![]() reprezinta definitia
miscarii oscilatorii armonice si poate fi obtinuta direct din legea a doua a
dinamicii:
reprezinta definitia
miscarii oscilatorii armonice si poate fi obtinuta direct din legea a doua a
dinamicii:
![]()
De aici rezulta ca acceleratia este intotdeauna de sens opus elongatiei, avand valoarea zero cand oscilatorul trece prin pozitia de echilibru, si valoarea maxima in momentele in care oscilatorul se afla la distanta maxima fata de pozitia de echilibru. Valoarea maxima a acceleratiei este:
![]() . (2.65)
. (2.65)
In fig.3 se mai poate observa cum se poate obtine
miscarea oscilatorie armonica liniara prin proiectarea pe una din axe a unei miscari circulare uniforme.
Astfel, elongatia ![]() , viteza
, viteza ![]() si acceleratia
si acceleratia ![]() se obtin
proiectand pe axa
se obtin
proiectand pe axa ![]() , la momentul
, la momentul ![]() , raza vectoare, viteza, si respectiv acceleratia normala
a punctului ce executa miscarea circulara. Se obtin astfel ecuatiile de miscare
sub forma:
, raza vectoare, viteza, si respectiv acceleratia normala
a punctului ce executa miscarea circulara. Se obtin astfel ecuatiile de miscare
sub forma:
![]() (2.66)
(2.66)
unde ![]() este amplitudinea
miscarii, iar viteza si acceleratia sunt:
este amplitudinea
miscarii, iar viteza si acceleratia sunt:
![]() (2.67)
(2.67)
![]()
(2.68)
Formulele (2.58), (2.59), (2.64), si respectiv
(2.66), (2.67), (2.68) reprezinta aceleasi legi de miscare, singura
deosebire fiind faptul ca in primele
trei formule apare ![]() , iar in ultimele trei apare
, iar in ultimele trei apare ![]() , in timp ce functiile sinus si cosinus se inverseaza
intre ele.
, in timp ce functiile sinus si cosinus se inverseaza
intre ele.


Exemplul 3.
La
momentele ![]() si
si ![]() , valorile corespunzatoare ale elongatiilor
, valorile corespunzatoare ale elongatiilor ![]() si
si ![]() ale unui oscilator
liniar armonic sunt legate intre ele
prin relatia
ale unui oscilator
liniar armonic sunt legate intre ele
prin relatia ![]() . Sa se determine valoarea minima a frecventei oscilatorului,
daca in momentul initial acesta se afla in pozitia de echilibru, iar
. Sa se determine valoarea minima a frecventei oscilatorului,
daca in momentul initial acesta se afla in pozitia de echilibru, iar ![]()
Rezolvare
Ecuatia de miscare a oscilatorului
este ![]() , iar din conditia problemei se obtine ecuatia trigonometrica
, iar din conditia problemei se obtine ecuatia trigonometrica
![]() .
.
Rezolvand
ecuatia obtinem, pentru ![]() ,
, 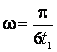 , respectiv
, respectiv ![]()
![]() .
.
Exemplul 4
Sa se determine amplitudinea, faza initiala si pulsatia proprie a unui
oscilator armonic liniar, cunoscand conditiile initiale: ![]() si
si ![]() la momentul
la momentul ![]()
Particularizand expresiile lui ![]() ,
, ![]() si
si ![]() din ecuatiile de
miscare:
din ecuatiile de
miscare: ![]() ,
, ![]() si
si ![]() la momentul
la momentul ![]() , obtinem sistemul de trei ecuatii cu trei necunoscute
, obtinem sistemul de trei ecuatii cu trei necunoscute ![]()
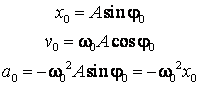
Din ultima ecuatie
se obtine direct 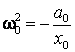 , iar din primele doua obtinem, prin rezolvarea sistemului:
, iar din primele doua obtinem, prin rezolvarea sistemului:

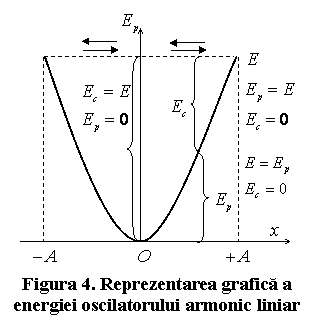
2 Energia oscilatorului armonic liniar
Energia oscilatorului armonic liniar
(pendulul elastic) se compune din energia cinetica a punctului material ![]() si energia potentiala
a resortului de care acesta este prins,
si energia potentiala
a resortului de care acesta este prins, ![]() . Cu
. Cu 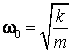 si
si ![]() obtinem
obtinem ![]() , respectiv
, respectiv ![]() . Valoarea maxima a lui
. Valoarea maxima a lui ![]() este se atinge la
trecerea prin pozitia de echilibru
este se atinge la
trecerea prin pozitia de echilibru 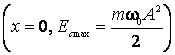 , iar a lui
, iar a lui ![]() in pozitia de
elongatie maxima
in pozitia de
elongatie maxima 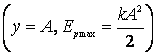 Energia
totala a oscilatorului armonic liniar va fi:
Energia
totala a oscilatorului armonic liniar va fi:
![]() (2.69)
(2.69)
Acest rezultat reprezinta
conservarea energiei oscilatorului armonic in timpul miscarii. Din (2.69)
rezulta de asemenea ca ![]() , adica in procesul de oscilatie energia cinetica a
oscilatorului trece continuu in energie potentiala si invers, suma lor ramanand
constanta in fiecare moment (fig.4).
, adica in procesul de oscilatie energia cinetica a
oscilatorului trece continuu in energie potentiala si invers, suma lor ramanand
constanta in fiecare moment (fig.4).
3 Pendulul elastic in camp gravitational
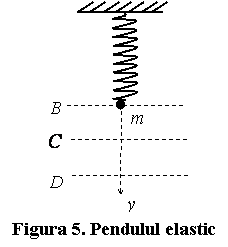 Presupunem un resort de constanta
elastica
Presupunem un resort de constanta
elastica ![]() in pozitie
verticala, fixat la capatul de sus. Sa stabilim ecuatia de miscare a unui corp
de masa
in pozitie
verticala, fixat la capatul de sus. Sa stabilim ecuatia de miscare a unui corp
de masa ![]() , care se fixeaza la momentul
, care se fixeaza la momentul ![]() de capatul liber
al resortului (fig.5). Asupra corpului actioneaza greutatea
de capatul liber
al resortului (fig.5). Asupra corpului actioneaza greutatea ![]() , si deci la momentul
, si deci la momentul ![]() corpul incepe sa
cada cu acceleratia
corpul incepe sa
cada cu acceleratia ![]() . Deoarece in acest moment in resort nu s-a creat inca o
forta elastica care sa se opuna greutatii, corpul tinde sa coboare accelerat.
Pe masura ce corpul se indeparteaza de nivelul
. Deoarece in acest moment in resort nu s-a creat inca o
forta elastica care sa se opuna greutatii, corpul tinde sa coboare accelerat.
Pe masura ce corpul se indeparteaza de nivelul ![]() (resortul
nedeformat) alungirea resortului incepe sa creasca, si o data cu aceasta va
creste si forta elastica, care este de sens opus greutatii. Pe masura ce
resortul se deformeaza forta elastica care se opune greutatii creste, ajungand
intr-o pozitie
(resortul
nedeformat) alungirea resortului incepe sa creasca, si o data cu aceasta va
creste si forta elastica, care este de sens opus greutatii. Pe masura ce
resortul se deformeaza forta elastica care se opune greutatii creste, ajungand
intr-o pozitie ![]() in care forta
elastica este egala si de sens contrar cu greutatea (
in care forta
elastica este egala si de sens contrar cu greutatea (![]() ). Deoarece pe distanta
). Deoarece pe distanta ![]() corpul s-a
deplasat accelerat, el are in punctul
corpul s-a
deplasat accelerat, el are in punctul ![]() o viteza maxima si nu
se opreste in acel punct, continuand sa se deplaseze incetinit pana in punctul de
oprire
o viteza maxima si nu
se opreste in acel punct, continuand sa se deplaseze incetinit pana in punctul de
oprire ![]() . Deoarece forta elastica in punctul
. Deoarece forta elastica in punctul ![]() devine dublul
greutatatii
devine dublul
greutatatii ![]() , corpul se va misca accelerat din
, corpul se va misca accelerat din ![]() in
in ![]() , apoi din nou
incetinit din
, apoi din nou
incetinit din ![]() in
in ![]() . In aceste conditii corpul va oscila in jurul punctului
. In aceste conditii corpul va oscila in jurul punctului ![]() cu amplitudinea
cu amplitudinea ![]() , care se obtine din conditia:
, care se obtine din conditia:
![]() (2.70)
(2.70)
Ecuatia de miscare a oscilatorului este, dupa formula generala,
![]()
unde 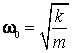 si
si ![]() , astfel ca ecuatia de miscare devine:
, astfel ca ecuatia de miscare devine:
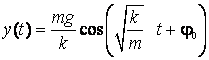 (2.71)
(2.71)
Faza initiala ![]() poate fi
determinata din conditiile initiale si este functie de sensul de orientare al
axei
poate fi
determinata din conditiile initiale si este functie de sensul de orientare al
axei ![]() . Daca axa
. Daca axa ![]() este orientata in
jos, atunci la
este orientata in
jos, atunci la ![]() si in consecinta
si in consecinta ![]() , de unde
, de unde ![]() si
si ![]() (fig.5). Daca axa
(fig.5). Daca axa ![]() este orientata in sus, atunci pentru
este orientata in sus, atunci pentru ![]()
![]() , de unde
, de unde ![]() si
si ![]() .
.
4 Pendulul matematic (gravitational)
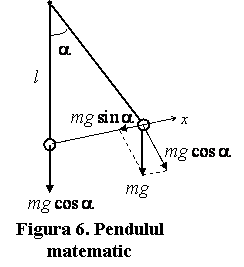 Pendulul gravitational reprezinta un
corp punctiform de masa
Pendulul gravitational reprezinta un
corp punctiform de masa ![]() , suspendat de un punct fix printr-un fir inextensibil de
lungime
, suspendat de un punct fix printr-un fir inextensibil de
lungime ![]() si greutate
neglijabila. Pozitia de echilibru a pendulului gravitational este cu firul in
pozitie verticala. Daca firul este scos din pozitia de echilibru, pentru
unghiuri mici cu verticala (
si greutate
neglijabila. Pozitia de echilibru a pendulului gravitational este cu firul in
pozitie verticala. Daca firul este scos din pozitia de echilibru, pentru
unghiuri mici cu verticala (![]() ), asupra corpului va actiona o forta cuasielastica care
tinde sa-l aduca in pozitia de echilibru prin executarea de oscilatii in jurul acestei
pozitii. Forta cuasielastica nu este de natura elastica, insa in anumite
conditii satisface cerintele impuse asupra fortei elastice. Pentru unghiuri
mici fata de verticala putem aproxima traiectoria punctului material cu o
dreapta paralela cu axa
), asupra corpului va actiona o forta cuasielastica care
tinde sa-l aduca in pozitia de echilibru prin executarea de oscilatii in jurul acestei
pozitii. Forta cuasielastica nu este de natura elastica, insa in anumite
conditii satisface cerintele impuse asupra fortei elastice. Pentru unghiuri
mici fata de verticala putem aproxima traiectoria punctului material cu o
dreapta paralela cu axa ![]() , si putem scrie cu buna aproximatie pentru o deplasare
, si putem scrie cu buna aproximatie pentru o deplasare ![]() fata de pozitia de
echilibru relatiile (fig.6):
fata de pozitia de
echilibru relatiile (fig.6):
![]()
Se ajunge astfel la
concluzia ca daca unghiul firului cu verticala in timpul miscarii este suficient
de mic, forta tangentiala care cauta sa readuca pendulul in pozitia de
echilibru este proportionala cu distanta ![]() fata de aceasta
pozitie, adica forta tangentiala are aceeasi proprietate ca si o forta
elastica. Astfel de forte cu actiune analoga fortei elastice se numesc forte cuasielastice. Astfel, pendulul
gravitational poate fi privit ca un pendul elastic asupra caruia actioneaza un
resort cu constanta elastica
fata de aceasta
pozitie, adica forta tangentiala are aceeasi proprietate ca si o forta
elastica. Astfel de forte cu actiune analoga fortei elastice se numesc forte cuasielastice. Astfel, pendulul
gravitational poate fi privit ca un pendul elastic asupra caruia actioneaza un
resort cu constanta elastica ![]() , avand pulsatia proprie
, avand pulsatia proprie
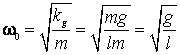 (2.73)
(2.73)
si perioada:
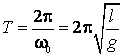 (2.74)
(2.74)
Comparand datele de la pendulul elastic si gravitational, in tabelul 1 se face o analogie interesanta a formulelor pentru pulsatia proprie, perioada si frecventa. In fine, din formula (2.74) rezulta cele 4 legi ale pendulului gravitational, stabilite de Galilei pe cale experimentala:
![]()
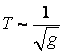
![]() nu depinde de
nu depinde de ![]()
![]() nu depinde de
nu depinde de ![]() (legea izocronismului micilor oscilatii).
(legea izocronismului micilor oscilatii).
Tabelul 1. Analogia dintre pendulul elastic si pendulul gravitational
|
Pendul elastic |
Pendul gravitational |
|
|
|
|
|
|
|
|
|
5 Compunerea oscilatiilor paralele de aceeasi pulsatie
In
unele cazuri un corp de masa ![]() este supus
concomitent actiunii a doua sau mai multor forte elastice. Miscarea acestui
corp este rezultanta miscarilor oscilatorii individuale pe care le-ar efectua
corpul sub actiunea fiecarei forte elastice in parte. Sa presupunem ca sub
actiunea fortelor elastice
este supus
concomitent actiunii a doua sau mai multor forte elastice. Miscarea acestui
corp este rezultanta miscarilor oscilatorii individuale pe care le-ar efectua
corpul sub actiunea fiecarei forte elastice in parte. Sa presupunem ca sub
actiunea fortelor elastice ![]() si
si ![]() corpul executa separat
miscarile oscilatorii (2.75) si (2.76)
corpul executa separat
miscarile oscilatorii (2.75) si (2.76)
![]() , (2.75)
, (2.75)
![]()
 Cele doua forte actionand
concomitent (simultan) asupra punctului material, acesta va executa o miscare,
de asemenea oscilatorie armonica, data de formula:
Cele doua forte actionand
concomitent (simultan) asupra punctului material, acesta va executa o miscare,
de asemenea oscilatorie armonica, data de formula:
![]() (2.77)
(2.77)
Problema compunerii miscarilor oscilatorii se
rezolva exprimand marimile ![]() si
si ![]() functie de
functie de ![]() si
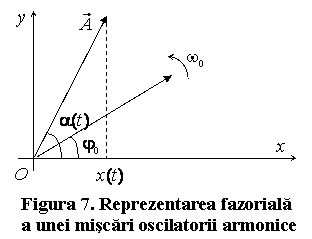
si ![]() . Cea mai buna metoda este bazata pe reprezentarea
fazoriala a miscarii oscilatorii (fig.7). Marimea (2.77) poate fi
reprezentata printr-un vector
. Cea mai buna metoda este bazata pe reprezentarea
fazoriala a miscarii oscilatorii (fig.7). Marimea (2.77) poate fi
reprezentata printr-un vector ![]() de lungime
de lungime ![]() , care la momentul
, care la momentul ![]() face cu axa
face cu axa ![]() unghiul
unghiul ![]() . Daca acest vector se roteste in jurul punctului
. Daca acest vector se roteste in jurul punctului ![]() cu viteza unghiulara
constanta
cu viteza unghiulara
constanta ![]() , proiectiile varfului sau pe axele
, proiectiile varfului sau pe axele ![]() si
si ![]() executa miscari oscilatorii.
executa miscari oscilatorii.
![]() ;
;
![]() .
.
In fig.8 se reprezinta
sub forma fazoriala miscarile (2.75) si (2.76), prin compunerea carora vom
obtine miscarea rezultanta (2.77). Proiectand relatia vectoriala ![]() pe cele doua axe,
obtinem sistemul de ecuatii:
pe cele doua axe,
obtinem sistemul de ecuatii:
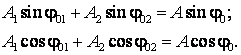
Prin impartirea ecuatiilor (2.78) obtinem:
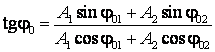 (2.79)
(2.79)
Ridicand la patrat ecuatiile (2.78) si adunandu-le, obtinem:
![]()
![]() (2.80)
(2.80)
Se observa ca amplitudinea rezultanta depinde atat
de amplitudinile ![]() si
si ![]() , cat si de diferenta dintre fazele initiale
, cat si de diferenta dintre fazele initiale ![]()
Se disting urmatoarele cazuri particulare:
a) ![]()
![]() . In acest caz oscilatiile sunt in faza, si prin
compunerea lor se obtine pentru miscarea oscilatorie rezultanta amplitudinea
maxima.
. In acest caz oscilatiile sunt in faza, si prin
compunerea lor se obtine pentru miscarea oscilatorie rezultanta amplitudinea
maxima.
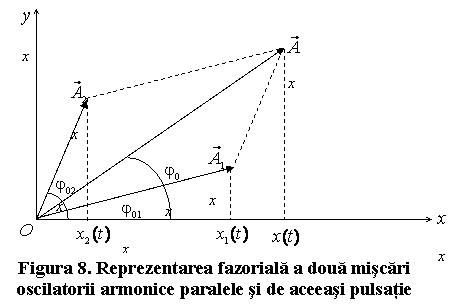
![]()
b) ![]() , unde
, unde ![]()
![]() . In acest caz se spune ca oscilatiile sunt in
cuadratura.
. In acest caz se spune ca oscilatiile sunt in
cuadratura.
c) ![]()
![]() . Oscilatiile sunt in opozitie de faza si amplitudinea
rezultanta este minima (daca
. Oscilatiile sunt in opozitie de faza si amplitudinea
rezultanta este minima (daca![]() , rezulta
, rezulta ![]() ). Astfel, prin compunerea a doua oscilatii in opozitie
de faza se obtine repaus, adica miscarile oscilatorii se anihileaza reciproc.
Asest caz prezinta un interes tehnic special, fiind singura posibilitate de
inlaturare a unor vibratii nedorite.
). Astfel, prin compunerea a doua oscilatii in opozitie
de faza se obtine repaus, adica miscarile oscilatorii se anihileaza reciproc.
Asest caz prezinta un interes tehnic special, fiind singura posibilitate de
inlaturare a unor vibratii nedorite.
Metoda reprezentarii fazoriale a miscarii oscilatorii permite generalizarea rezultatelor de la compunerea a doua oscilatii la compunerea mai multor oscilatii. Astfel, pentru compunerea a trei unde formulele amplitudinii si fazei initiale a oscilatiei rezultante (2.79) si (2.80) devin:
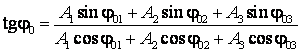
![]()
6 Compunerea oscilatiilor perpendiculare de aceeasi pulsatie
Sa
consideram un punct material supus concomitent actiunii a doua forte elastice
actionand pe directii perpendiculare. Sub actiunea acestor forte punctul
material va efectua doua miscari oscilatorii de aceeasi pulsatie, insa cu faze
initiale diferite. Alegand pentru cele doua directii perpendiculare axele ![]() si
si ![]() , ecuatiile celor doua miscari oscilatorii vor fi:
, ecuatiile celor doua miscari oscilatorii vor fi:
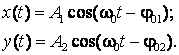
Ecuatia traiectoriei punctului supus simultan
actiunii celor doua forte elastice se deduce eliminand timpul ![]() intre ecuatiile (2.83).
Rescriem ecuatiile sub forma:
intre ecuatiile (2.83).
Rescriem ecuatiile sub forma:
 (2.84)
(2.84)
Din sistemul (2.84) obtinem expresiile lui ![]() si
si ![]() sub forma:
sub forma:
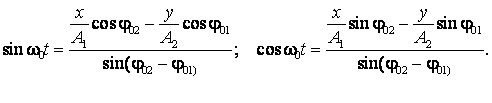 (2.85)
(2.85)
Vom nota cu ![]() diferenta dintre
fazele initiale ale celor doua oscilatii.
diferenta dintre
fazele initiale ale celor doua oscilatii.
Pentru a elimina timpul intre ecuatiile (2.83)
ridicam la patrat expresiile (2.85), apoi le adunam folosind identitatea
trigonometrica ![]()
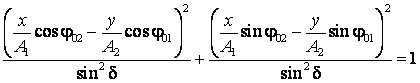
si printr-un calcul trigonometric simplu se obtine:
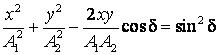 (2.86)
(2.86)
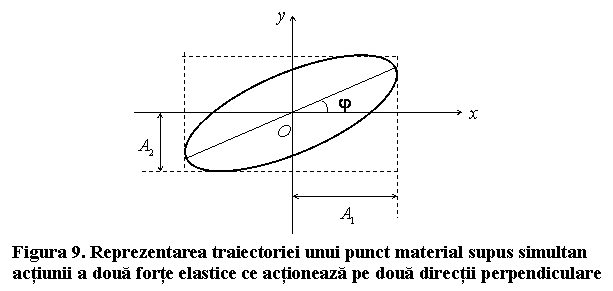
Relatia (2.86) reprezinta ecuatia unei elipse
cuprinsa intr-un dreptunghi de laturi ![]() si
si ![]() (fig.9). Se
remarca urmatoarele cazuri particulare:
(fig.9). Se
remarca urmatoarele cazuri particulare:
a) ![]() , unde
, unde ![]() este un numar
intreg, si ecuatia (2.86) devine:
este un numar
intreg, si ecuatia (2.86) devine:
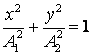 (2.87)
(2.87)
Reprezintand o elipsa cu axa mare ![]() si axa mica
si axa mica ![]() , iar axele de coordonate
, iar axele de coordonate ![]() si
si ![]() axe principale ale
elipsei (fig.10).
axe principale ale
elipsei (fig.10).
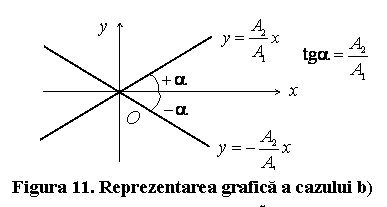
b) ![]() ; in acest caz obtinem din ecuatia (2.86):
; in acest caz obtinem din ecuatia (2.86):
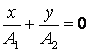 daca
daca ![]() este impar,
respectiv
este impar,
respectiv 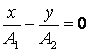 daca
daca ![]() este par.
este par.
Astfel, elipsa degenereaza intr-o dreapta (fig.11).
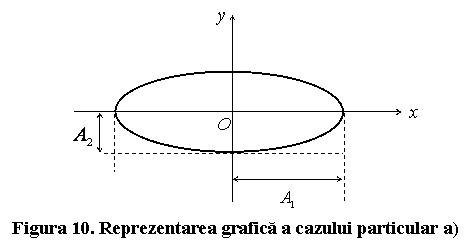

In general, putem spune ca un punct material supus concomitent la doua miscari oscilatorii de aceeasi pulsatie, ce au loc pe doua directii perpendiculare, se va deplasa pe o traiectorie eliptica. Sensul miscarii pe elipsa se poate determina in functie de diferenta de faza dintre cele doua miscari oscilatorii. Acest subiect are aplicatii in mai multe domenii ale fizicii, printre care si in optica, la polarizarea undelor electromagnetice.

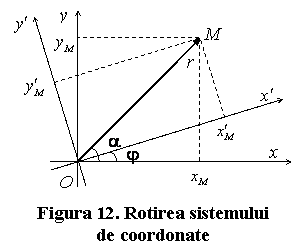
Pentru
a determina unghiul ![]() dintre axa mare a
elipsei si axa
dintre axa mare a
elipsei si axa ![]() din fig.9 efectuam o
rotatie de unghi
din fig.9 efectuam o
rotatie de unghi ![]() a sistemului de coordonate
a sistemului de coordonate ![]() . Apoi deducem relatiile dintre
acestea si coordonatele sistemului rotit
. Apoi deducem relatiile dintre
acestea si coordonatele sistemului rotit ![]() (fig.12) pentru un punct oarecare M. In relatiile ce urmeaza vom renunta la
indicele M.
(fig.12) pentru un punct oarecare M. In relatiile ce urmeaza vom renunta la
indicele M.
![]()
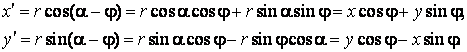 (2.88)
(2.88)
Din (2.88) determinam pe ![]() si
si ![]() in functie de
in functie de ![]() si
si ![]() si obtinem:
si obtinem:
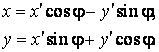
Introducem (2.89) in (2.86), obtinand ecuatia
elipsei in coordonate ![]() , caz in care semiaxa mare, respectiv semiaxa mica, vor
coincide cu directia axei de coordonate rotite
, caz in care semiaxa mare, respectiv semiaxa mica, vor
coincide cu directia axei de coordonate rotite ![]() , respectiv
, respectiv ![]() . In noua forma a ecuatiei elipsei, termenul care contine
produsul
. In noua forma a ecuatiei elipsei, termenul care contine
produsul ![]() va fi:
va fi:
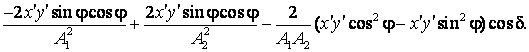
Anulam coeficientul termenului care contine
produsul ![]() si obtinem:
si obtinem:
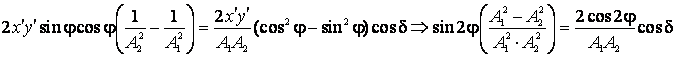 care se poate scrie mai simplu sub forma
care se poate scrie mai simplu sub forma
 (2.90)
(2.90)
 Exemplul
5
Exemplul
5
Un corp punctiform efectueaza
simultan doua miscari oscilatorii pe doua axe perpendiculare Ox si Oy, cu
ecuatiile ![]() , respectiv
, respectiv ![]() . Daca
. Daca ![]() rad/s, sa se determine valorile vitezei si acceleratiei
corpului la momentul
rad/s, sa se determine valorile vitezei si acceleratiei
corpului la momentul ![]() (
(![]() este perioada de oscilatie).
este perioada de oscilatie).
Rezolvare
Din ![]() si
si ![]() rezulta:
rezulta:
![]()
Din ![]() si
si ![]() rezulta:
rezulta:
![]()
Identificand expresia analitica a produsului scalar dintre vectorii viteza si acceleratie:
![]()
cu formula de definitie a produsului scalar:
![]() ,
,
se obtine:
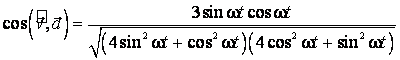
La
momentul ![]() si pentru
si pentru ![]() se obtine
se obtine ![]() , si astfel unghiul dinttre viteza si acceleratie va fi:
, si astfel unghiul dinttre viteza si acceleratie va fi:
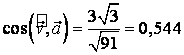 .
.
7 Miscarea oscilatorie amortizata
In general, un punct material asupra caruia actioneaza o forta elastica intampina in miscarea sa rezistenta mediului, prin actiunea unei forte de frecare. Forma analitica a fortei de frecare este greu de dedus in cazul general. Daca insa consideram forta de frecare proportionala cu viteza corpului si orientata in sens opus miscarii, vom obtine rezultate in buna concordanta cu experimentele. In aceste conditii legea a doua a dinamicii se scrie astfel:
![]()
unde
![]() (2.92)
(2.92)
si ![]() este o marime
strict pozitiva. Inlocuind (2.92) in (2.91) se obtine:
este o marime
strict pozitiva. Inlocuind (2.92) in (2.91) se obtine:
![]() (2.93)
(2.93)
Introducem notatia
![]() (2.94)
(2.94)
unde ![]() se numeste
coeficient de amortizare. Din (2.93) obtinem:
se numeste
coeficient de amortizare. Din (2.93) obtinem:
![]() (2.95)
(2.95)
Cautam solutia ecuatiei (2.95) sub forma:
![]() (2.96)
(2.96)
unde ![]() este o
este o ![]() si
si ![]() in (2.95), obtinand
ecuatia caracteristica:
in (2.95), obtinand
ecuatia caracteristica:
![]() , (2.97)
, (2.97)
cu radacinile
![]() . (2.98)
. (2.98)
Pentru a avea o miscare
oscilatorie, radacinile ![]() si
si ![]() trebuie sa fie numere
imaginare, deoarece numai in acest caz miscarea este limitata in spatiu.
Aceasta cerinta este satisfacuta numai cand coeficientul de amortizare
trebuie sa fie numere
imaginare, deoarece numai in acest caz miscarea este limitata in spatiu.
Aceasta cerinta este satisfacuta numai cand coeficientul de amortizare ![]() este mai mic decat
pulsatia proprie
este mai mic decat
pulsatia proprie ![]() , caz in care putem scrie
, caz in care putem scrie
![]() (2.99)
(2.99)
Solutia generala a ecuatiei diferentiale (2.95) devine astfel:
![]() (2.100)
(2.100)
Solutia generala a unei
ecuatii diferentiale de gradul doi contine doua constante de integrare. Elongatia
miscarii oscilatorii ![]() fiind o marime reala,
cele doua constante
fiind o marime reala,
cele doua constante ![]() si
si ![]() trebuie sa fie numere
complexe. Pentru doua numere complexe exista doua numere reale
trebuie sa fie numere
complexe. Pentru doua numere complexe exista doua numere reale ![]() si
si ![]() astfel ca sa fie
indeplinite relatiile:
astfel ca sa fie
indeplinite relatiile:
![]() (2.101)
(2.101)
Cu aceste notatii solutia (2.100) poate fi scrisa sub forma:
![]() (2.102)
(2.102)
Folosind relatiile lui Euler (2.57) se obtine legea de miscare a punctului material supus unei forte elastice, cat si fortei de frecare:
![]() (2.103)
(2.103)
unde
![]()
reprezinta pulsatia miscarii amortizate.
Prezenta amortizarii conduce la urmatoarele doua efecte importante:
- pulsatia
miscarii amortizate este intotdeauna mai mica decat cea a miscarii neamortizate, si depinde de valoarea
coeficientului de amortizare ![]()
- amplitudinea miscarii, si deci energia oscilatorului, scad exponential in timp, pana cand in final corpul se opreste.


In fig.13, respectiv 14, se reprezinta
elongatia unei miscari oscilatorii armonice fara amortizare, respectiv cu
amortizare. Prezenta amortizarii conduce
la scaderea amplitudinii, si deci in final la incetarea miscarii oscilatorului.
Se observa din (2.103) ca dupa un interval de timp ![]() , denumit durata de
relaxare a oscilatiei amortizate, amplitudinea miscarii oscilatorii scade
de '
, denumit durata de
relaxare a oscilatiei amortizate, amplitudinea miscarii oscilatorii scade
de '![]() ' ori, iar energia oscilatorului de '
' ori, iar energia oscilatorului de '![]() ' ori. In general o miscare oscilatorie armonica amortizata
este caracterizata prin decrementul logaritmic
' ori. In general o miscare oscilatorie armonica amortizata
este caracterizata prin decrementul logaritmic ![]() :
:
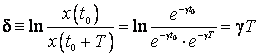 (2.105)
(2.105)
care se mai poate scrie si sub forma:
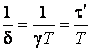 (2.106)
(2.106)
De aici rezulta
semnificatia fizica a decrementului logaritmic: inversul decrementului
logaritmic reprezinta numarul de oscilatii complete efectuate de oscilator in
intervalul de timp in care amplitudinea scade de '![]() ' ori.
' ori.
Miscarea oscilatorie armonica este
un caz particular al miscarii oscilatorii amortizate in cazul limita ![]() , cand din relatia (2.103) obtinem ecuatia de miscare a
oscilatorului armonic
, cand din relatia (2.103) obtinem ecuatia de miscare a
oscilatorului armonic ![]() . La oscilatorul armonic amplitudinea
. La oscilatorul armonic amplitudinea ![]() este constanta, iar
energia se conserva in timp:
este constanta, iar
energia se conserva in timp:
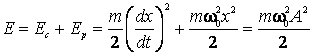


Pentru ca un punct material sa poata efectua miscari oscilatorii fiind supus unor forte de frecare (amortizare), este necesar ca asupra sa sa actioneze o forta exterioara periodica (excitator), adica oscilatiile sa fie intretinute sau fortate. Rolul fortei exterioare de intretinere este acela de a suplini, prin lucrul mecanic efectuat, pierderile de energie datorate amortizarii. Este foarte important momentul si sensul in care in care actioneaza periodic forta de intretinere. Transferul de energie de la excitator la sistemul excitat, care se face in fiecare perioada a excitatorului, este maxim cand pulsatia excitatorului este apropiata de pulsatia proprie a sistemului excitat. Procesul selectiv de transfer de energie intre doua sisteme fizice se numeste rezonanta.
Exemplul 6
Sa se determine
decrementul logaritmic al miscarii amortizate pentru un oscilator cu frecventa
proprie ![]() , daca frecventa miscarii amortizate este
, daca frecventa miscarii amortizate este ![]() .
.
Rezolvare
Din relatiile cunoscute ![]() rezulta:
rezulta:
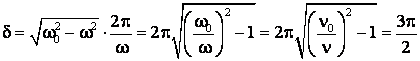 .
.
8 Miscarea oscilatorie intretinuta
Energia unui oscilator fiind proportionala cu patratul amplitudinii, prezenta fortelor de frecare la un oscilator amortizat conduce la scaderea energiei medii in timp dupa legea:
![]() (2.107)
(2.107)
Pentru a mentine
constanta energia oscilatorului, energia pierduta trebuie recuperata prin actiunea
unei forte periodice ![]() , pe care pentru simplitate o vom presupune de forma:
, pe care pentru simplitate o vom presupune de forma:
![]() (2.108)
(2.108)
Daca asupra punctului material din
fig.2 actioneaza forta elastica ![]() , forta de franare
, forta de franare ![]() si forta
exterioara de intretinere
si forta
exterioara de intretinere ![]() , ecuatia diferentiala a miscarii oscilatorului va fi :
, ecuatia diferentiala a miscarii oscilatorului va fi :
![]() (2.109)
(2.109)
Introducand
expresiile fortelor si impartind la ![]() , obtinem ecuatia diferentiala de gradul al doilea,
neomogena si cu coeficienti constanti:
, obtinem ecuatia diferentiala de gradul al doilea,
neomogena si cu coeficienti constanti:
![]() (2.110)
(2.110)
Solutia acestei
ecuatii este suma dintre solutia ecuatiei omogene (2.103) si o expresie de
forma termenului liber ![]() . Datorita scaderii exponentiale a amplitudinii in timp, solutia
ecuatiei omogene devine neglijabila dupa timpul
. Datorita scaderii exponentiale a amplitudinii in timp, solutia
ecuatiei omogene devine neglijabila dupa timpul ![]() , si se cauta pentru ecuatia diferentiala (2.110) o solutie
de forma:
, si se cauta pentru ecuatia diferentiala (2.110) o solutie
de forma:
![]() , (2.111)
, (2.111)
unde ![]() nu depinde de timp si
se determina introducand (2.111), ca si derivatele
nu depinde de timp si
se determina introducand (2.111), ca si derivatele ![]()
![]() , in ecuatia (2.110):
, in ecuatia (2.110):
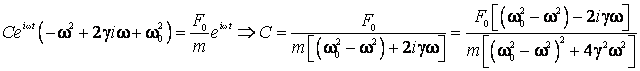 Aceasta expresie mai poate fi scrisa sub forma :
Aceasta expresie mai poate fi scrisa sub forma :
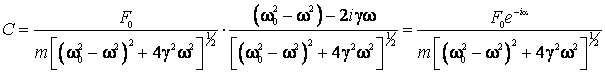 (2.112)
(2.112)
Pe baza formulelor (2.57) se obtine:
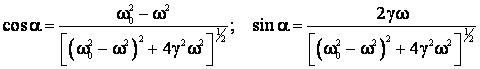 ,
,
de unde rezulta:
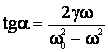 (2.113)
(2.113)
Solutia ecuatiei diferentiale (2.110) devine astfel:
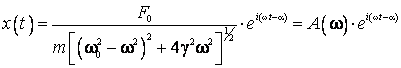 (2.114)
(2.114)
Se poate observa
usor in fig. 15 ca intre elongatia ![]() si forta exterioara
si forta exterioara ![]() apare o diferenta de
faza
apare o diferenta de
faza ![]() , cu valori cuprinse intre
, cu valori cuprinse intre ![]() si
si ![]() .
.
Amplitudinea miscarii este data de expresia:
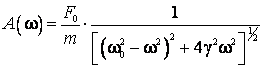 , (2.115)
, (2.115)
si prezinta un
maximum pentru pulsatia ![]() (pulsatia de
rezonanta, care se obtine din conditia ca termenul de la numitor sa fie minim):
(pulsatia de
rezonanta, care se obtine din conditia ca termenul de la numitor sa fie minim):
![]() (2.116)
(2.116)
Pulsatia la rezonanta
![]() nu este egala cu
pulsatia proprie
nu este egala cu
pulsatia proprie ![]() a sistemului, ci
depinde de coeficientul de amortizare
a sistemului, ci
depinde de coeficientul de amortizare ![]() .
.

In fig.16 este
indicata aproximativ dependenta ![]() , pentru valori diferite ale parametrului
, pentru valori diferite ale parametrului ![]() . Introducand (2.116) in (2.115) obtinem amplitudinea la
rezonanta
. Introducand (2.116) in (2.115) obtinem amplitudinea la
rezonanta ![]() :
:
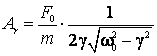 (2.117)
(2.117)
Se observa ca amplitudinea la rezonanta este cu atat mai mare cu cat coeficientul de amortizare este mai mic. Fenomenul de rezonanta are aplicatii multiple in stiinta si tehnica, fiind in unele cazuri deosebit de util, iar in alte cazuri daunator.


Exemplul 7
Sa aratam cum se determina
pulsatia de rezonanta a unui oscilator intretinut, daca pentrua doua pulsatii ![]() si
si ![]() amplitudinea
oscilatiilor are aceeasi valoare.
amplitudinea
oscilatiilor are aceeasi valoare.
Rezolvare
Folosind (2.115), din conditia ![]() obtinem:
obtinem:
![]() ,
,
Rezolvand ecuatia, obtinem dupa calcule simple:
![]() ,
,
Tinand cont de (2.116) se obtine
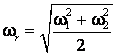 .
.
Bibliografie
1. Murray R. Spiegel. Schaum's outline of Theory and Problems of Theoretical Mechanics McGraw-Hill Book Company, New York,
2. David Halliday and Robert Resnick. Fizica vol.I, Ed. Didactica si Pedagogica, Bucuresti, 1975.
3. Frank S. Crawford, Jr. Cursul de Fizica Berkeley. Unde. vol.III, Ed. Didactica si Pedagogica, Bucuresti, 1983.
4. Richard P. Feynman, Robert B. Leighton and Matthew Sands. The Feynman Lectures on Physics vol.I, Definitive edition, Addison-Wesley Publishing Company, Reading, Massachusetts, 2006.
I. Irodov,
6. Traian I. Cretu. Fizica Generala vol.I. Editura Tehnica, Bucuresti, 1986.
7. Dan G. Siposen. Culegere de probleme de fizica. Editura Academiei Tehnice Militare, Bucuresti, 1999.