Probleme
P.1.1. Un
corp de masa m se poate deplasa fara
frecare pe o bara orizontala OA, care se roteste cu viteza unghiulara constanta
![]() in plan orizontal, in
jurul punctului O (fig. P.1.1.1). Folosind formalismul Lagrange sa se determine
legea de miscare a corpului neglijand masa barei.
in plan orizontal, in
jurul punctului O (fig. P.1.1.1). Folosind formalismul Lagrange sa se determine
legea de miscare a corpului neglijand masa barei.
Rezolvare. Punctul A are trei grade de libertate si o legatura si
deci doua coordonate generalizate care se aleg ![]() si
si ![]() (fig. P.1.1.1).
(fig. P.1.1.1).
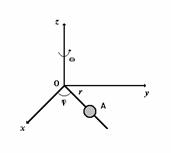
Fig. P.1.1.1. Bara si corpul A care se rote sc in plan orizontal.
Energia cinetica, potentiala si functia Lagrange sunt date de relatiile:
![]() , (P.1.1.1)
, (P.1.1.1)
![]() ,
(P.1.1.2)
,
(P.1.1.2)
![]() , (P.1.1.3)
, (P.1.1.3)
unde ![]() si
si ![]() .
.
Intrucat ![]() functia Lagrange (P.1.1.3), devine:
functia Lagrange (P.1.1.3), devine:
![]() (P.1.1.4)
(P.1.1.4)
sinand seama de relatia (P.1.1.4) in ecuatia Lagrange
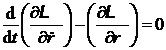 (P.1.1.5)
(P.1.1.5)
se obtine ecuatia de miscare sub forma:
![]() (P.1.1.6)
(P.1.1.6)
Solutia ecuatiei (P.1.1.6) este:
![]() (P.1.1.7)
(P.1.1.7)
Constantele ![]() si
si ![]() se determina din conditiile initiale.
se determina din conditiile initiale.
P.1.2. Un punct material A de masa ![]() se misca de-a lungul unei drepte OA
care formeaza unghiul
se misca de-a lungul unei drepte OA
care formeaza unghiul ![]() cu axa
cu axa ![]() (fig. P.1.2.1). Sa se determine
variatia in timp a unghiului polar,
(fig. P.1.2.1). Sa se determine
variatia in timp a unghiului polar, ![]() astfel ca miscarea punctului M sa
fie definita de ecuatia
astfel ca miscarea punctului M sa
fie definita de ecuatia ![]() , unde
, unde ![]() si
si ![]() sunt constante.
sunt constante.
Rezolvare. Punctul A are doua grade de libertate care se aleg ![]() si
si ![]() (fig. P.1.2.1). Energia cinetica, potentiala si functia Lagrange se calculeaza
cu ajutorul relatiilor:
(fig. P.1.2.1). Energia cinetica, potentiala si functia Lagrange se calculeaza
cu ajutorul relatiilor:
![]() (P.1.2.1)
(P.1.2.1)
![]() (P.1.2.2)
(P.1.2.2)
![]() (P.1.2.3)
(P.1.2.3)
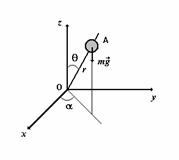
Fig. P.1.2.1.
Bara si corpul A care se rote sc in jurul axei ![]() .
.
Ecuatia Lagrange pentru
variabila ![]()
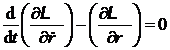 (P.1.2.4)
(P.1.2.4)
se scrie sub forma:
![]() (P.1.2.5)
(P.1.2.5)
Inlocuind solutia ![]() din datele problemei in ecuatia
(P.1.2.5) rezulta:
din datele problemei in ecuatia
(P.1.2.5) rezulta:
![]() (P.1.2.6)
(P.1.2.6)
de unde se obtine
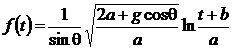 (P.1.2.7)
(P.1.2.7)
Daca in solutia (P.1.2.7)
se considera ![]() rezulta
rezulta ![]() , iar dreapta OA ramane fixa.
, iar dreapta OA ramane fixa.
P.1.3. Functia Lagrange a unei particule este
![]() (P.1.3.1)
(P.1.3.1)
unde ![]() reprezinta coordonata generalizata,
iar
reprezinta coordonata generalizata,
iar ![]() sunt constante pozitive. Sa se
calculeze: a) legea de miscare a particulei; b) functia Hamilton.
sunt constante pozitive. Sa se
calculeze: a) legea de miscare a particulei; b) functia Hamilton.
Rezolvare a) Inlocuind lagrangeanul ![]() dat de relatia (P.1.3.1) in ecuatia
Lagrange pentru variabila
dat de relatia (P.1.3.1) in ecuatia
Lagrange pentru variabila ![]()
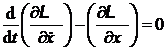 (P.1.3.2)
(P.1.3.2)
rezulta:
![]() (P.1.3.3)
(P.1.3.3)
unde constantele ![]() se pot determina din conditiile initiale.
Miscarea descrisa de legea (P.1.3.3) este uniform accelerata cu acceleratia
se pot determina din conditiile initiale.
Miscarea descrisa de legea (P.1.3.3) este uniform accelerata cu acceleratia ![]()
b) Hamiltonianul particulei se calculeaza cu ajutorul relatiei:
![]() (P.1.3.4)
(P.1.3.4)
unde
![]() (P.1.3.5)
(P.1.3.5)
reprezinta impulsul particulei. In final se obtine functia Hamilton sub forma:
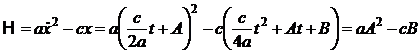 . (P.1.3.6)
. (P.1.3.6)
P.1.4.
Folosind formalismul Hamilton sa se deduca: a) expresia hamiltonianului si b)
ecuatia de miscare a unui electron de sarcina ![]() si masa
si masa ![]() , care se misca in campul de forte creat de nucleul de
hidrogen presupus fix. Se considera ca miscarea electronului are loc in planul
, care se misca in campul de forte creat de nucleul de
hidrogen presupus fix. Se considera ca miscarea electronului are loc in planul ![]()
Rezolvare. a) In coordonate polare
![]() ,
, ![]() , (P.1.4.1)
, (P.1.4.1)
energia cinetica, potentiala si functia Lagrange sunt date de relatiile:
![]() ,
(P.1.4.2)
,
(P.1.4.2)
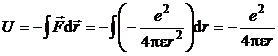 (P.1.4.3)
(P.1.4.3)
si respectiv
![]() . (P.1.4.4)
. (P.1.4.4)
Din
expresiile impulsurilor generalizate, ![]() si
si ![]() corespunzatoare
coordonatelor generalizate
corespunzatoare
coordonatelor generalizate ![]() si
si ![]() :
:
![]() si
si ![]() (P.1.4.5)
(P.1.4.5)
se obtine:
![]() si
si 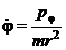 (P.1.4.6)
(P.1.4.6)
sinand seama de relatia (P.1.4.6), hamiltonianul sistemului se poate scrie sub forma:
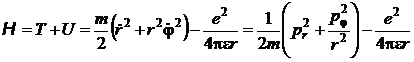 (P.1.4.7)
(P.1.4.7)
b) Din ecuatiile Hamilton
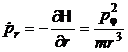
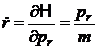 (P.1.4.8)
(P.1.4.8)
![]()
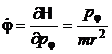 , (P.1.4.9)
, (P.1.4.9)
si ![]() se obtine in final ecuatia de miscare:
se obtine in final ecuatia de miscare:
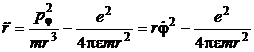 (P.1.4.10)
(P.1.4.10)
P.1.5. Functia Hamilton a unei particule este data de relatia:
![]() (P.1.5.1)
(P.1.5.1)
unde ![]() reprezinta deplasarea particulei,
reprezinta deplasarea particulei, ![]() este impulsul particulei si
este impulsul particulei si ![]() sunt constante pozitive. Sa se
determine: a) legea de miscare a particulei si b) traiectoria punctului
figurativ al miscarii in spatiul fazelor.
sunt constante pozitive. Sa se
determine: a) legea de miscare a particulei si b) traiectoria punctului
figurativ al miscarii in spatiul fazelor.
Rezolvare. a) Prin eliminarea impulsului din ecuatiile Hamilton
![]() (P.1.5.2)
(P.1.5.2)
![]() (P.1.5.3)
(P.1.5.3)
se obtine ecuatia de miscare a particulei sub forma:
![]() (P.1.5.4)
(P.1.5.4)
b) sinand seama de solutia ecuatiei (P.1.5.4)
![]() (P.1.5.5)
(P.1.5.5)
unde ![]() , expresia impulsului devine
, expresia impulsului devine
![]() (P.1.5.6)
(P.1.5.6)
Eliminand timpul intre ecuatiile (P.1.5.5) si (P.1.5.6) rezulta ecuatia traiectoriei punctului figurativ al miscarii in spatiul fazelor:
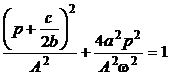 ,
(P.1.5.7)
,
(P.1.5.7)
care reprezinta o elipsa.
P.1.6. Se considera o sfera de raza ![]() care executa oscilatii
rostogolindu-se fara alunecare in interiorul unui cilindru avand raza
care executa oscilatii
rostogolindu-se fara alunecare in interiorul unui cilindru avand raza ![]() (fig. P.1.6.1).
Folosind formalismul Lagrange sa se deduca: a) ecuatia de miscare a sferei si
b) perioada micilor oscilatii.
(fig. P.1.6.1).
Folosind formalismul Lagrange sa se deduca: a) ecuatia de miscare a sferei si
b) perioada micilor oscilatii.
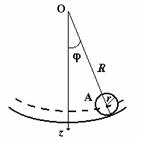
Fig. P.1.6.1.
Reprezentarea schematica a miscarii sferei in cilindrul de raza ![]() .
.
Rezolvare. a) Pentru a caracteriza miscarea sferei se introduce o
singura coordonata generalizata, ![]() (fig. P.2.8.1).
Energia cinetica, potentiala si functia Lagrange se calculeaza din relatiile:
(fig. P.2.8.1).
Energia cinetica, potentiala si functia Lagrange se calculeaza din relatiile:
![]() , (P.1.6.1)
, (P.1.6.1)
unde ![]() , iar
, iar ![]() este momentul de inertie
al sferei,
este momentul de inertie
al sferei,
![]() , (P.1.6.2)
, (P.1.6.2)
![]() (P.1.6.3)
(P.1.6.3)
Inlocuind relatia
(P.1.6.3) in ecuatia Lagrange pentru variabila ![]()
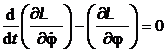 (P.1.6.4)
(P.1.6.4)
rezulta ecuatia de miscare a sferei de raza ![]()
![]() (P.1.6.5)
(P.1.6.5)
b) In cazul micilor oscilatii,
![]() ecuatia (P.1.6.5) devine:
ecuatia (P.1.6.5) devine:
![]() , (P.1.6.6)
, (P.1.6.6)
perioada acestora fiind:
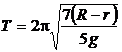 . (P.1.6.7)
. (P.1.6.7)
P.1.7. Sa se
calculeze: a) functia Lagrange si b) paranteza Poisson dintre ![]() si
si ![]() in cazul unei
particule pentru care functia Hamilton este data de relatia:
in cazul unei
particule pentru care functia Hamilton este data de relatia:
![]() (P.1.7.1)
(P.1.7.1)
unde ![]() reprezinta deplasarea particulei,
reprezinta deplasarea particulei, ![]() este impulsul particulei si
este impulsul particulei si ![]() sunt constante pozitive.
sunt constante pozitive.
Rezolvare. a) Functia Lagrange este data de relatia:
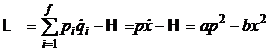 (P.1.7.2)
(P.1.7.2)
unde ![]() si
si ![]() reprezinta impulsurile si respectiv
vitezele generalizate, iar in cazul problemei de mai sus:
reprezinta impulsurile si respectiv
vitezele generalizate, iar in cazul problemei de mai sus:
![]() (P.1.7.3)
(P.1.7.3)
b) sinand seama de relatia de definitie a parantezelor Poisson
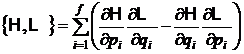 (P.1.7.4)
(P.1.7.4)
se obtine in final
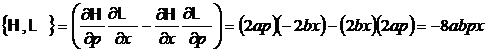 . (P.1.7.5)
. (P.1.7.5)
P.1.8. Se considera un corp de
masa ![]() aflat in cadere libera
aflat in cadere libera ![]() . Stiind ca la momentul initial
. Stiind ca la momentul initial ![]() corpul se afla in repaus, sa se
calculeze: a) valoarea integralei de actiune,
corpul se afla in repaus, sa se
calculeze: a) valoarea integralei de actiune, ![]() dupa
dupa ![]() secunde de cadere si b) sa se
compare valoarea acesteia cu cea corespunzatoare unei miscari virtuale in care
inaltimea pe care cade corpul creste liniar cu timpul.
secunde de cadere si b) sa se
compare valoarea acesteia cu cea corespunzatoare unei miscari virtuale in care
inaltimea pe care cade corpul creste liniar cu timpul.
Rezolvare a) Actiunea este data de relatia:
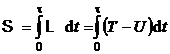 (P.1.8.1)
(P.1.8.1)
In cazul caderii libere ![]() , se obtine:
, se obtine:
![]() , (P.1.8.2)
, (P.1.8.2)
iar
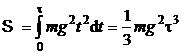 . (P.1.8.3)
. (P.1.8.3)
b) In cazul cand inaltimea de cadere variaza liniar cu
timpul, ![]() , unde
, unde ![]() este o constanta
pozitiva care se determina din conditia ca la extremitati cele doua integrale sa
coincida,
este o constanta
pozitiva care se determina din conditia ca la extremitati cele doua integrale sa
coincida,
![]() , de unde
, de unde ![]() (P.1.8.4)
(P.1.8.4)
rezulta
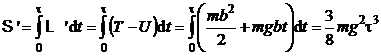 (P.1.8.5)
(P.1.8.5)
Comparand relatiile (P.1.8.3)
si (P.1.8.5) se observa ca ![]() , in concordanta cu principiul minimei actiuni.
, in concordanta cu principiul minimei actiuni.
P.2.1. O
incinta paralelipipedica cu volumul ![]() contine un gaz ideal
contine un gaz ideal ![]() la presiunea
la presiunea 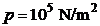 (fig. P.2.1).
(fig. P.2.1).
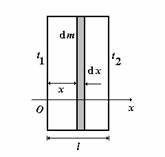
Fig. P.2.1. Incinta cu gaz ideal.
Stiind ca in interiorul incintei temperatura intre
doi pereti opusi variaza liniar de la ![]() la
la ![]() sa se calculeze masa de gaz aflata
in incinta. Se da constanta universala a gazelor
sa se calculeze masa de gaz aflata
in incinta. Se da constanta universala a gazelor ![]()
Rezolvare Intrucat temperatura gazului din interiorul incintei
variaza liniar cu distanta ![]()
![]() (P.2.1.1)
(P.2.1.1)
unde ![]() si
si ![]() se determina din conditiile la limita,
masa de gaz se calculeaza cu ajutorul relatiei:
se determina din conditiile la limita,
masa de gaz se calculeaza cu ajutorul relatiei:
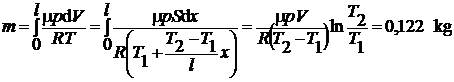 (P.2.1.2)
(P.2.1.2)
P.2.2. Un gaz ideal aflat initial la
presiunea ![]() si temperatura
si temperatura ![]() se destinde dupa legea:
se destinde dupa legea:
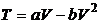 (P.2.2.1)
(P.2.2.1)
unde ![]() si
si ![]() sunt constante. Se cere sa se
calculeze: a) variatia energiei interne a
sunt constante. Se cere sa se
calculeze: a) variatia energiei interne a ![]() kmoli de gaz atunci cand volumul sau
creste de doua ori; b) lucrul mecanic efectuat de gaz in cursul destinderii de
la punctul a) al problemei. Se cunosc: exponentul adiabatic,
kmoli de gaz atunci cand volumul sau
creste de doua ori; b) lucrul mecanic efectuat de gaz in cursul destinderii de
la punctul a) al problemei. Se cunosc: exponentul adiabatic, ![]() si constanta universala a gazelor,
si constanta universala a gazelor,
![]()
Rezolvare a) Variatia energiei interne a gazului ideal este
![]() .
(P.2.2.2)
.
(P.2.2.2)
sinand seama de expresia
exponentul adiabatic 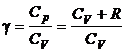 si de ecuatia de stare a gazului
ideal
si de ecuatia de stare a gazului
ideal ![]() , cu datele problemei
, cu datele problemei ![]() se obtine succesiv:
se obtine succesiv:
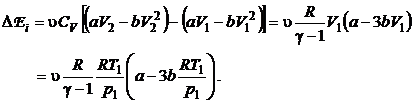 (P.2.2.3)
(P.2.2.3)
b) Lucrul mecanic efectuat de gaz se poate calcula cu ajutorul relatiei:
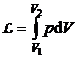 (P.2.2.4)
(P.2.2.4)
unde
![]() (P.2.2.5)
(P.2.2.5)
sinand seama de relatiile (P.2.2.4) si (P.2.2.5) rezulta:
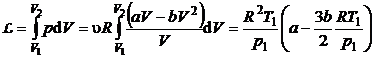 (P.2.2.6)
(P.2.2.6)
P.2.3. Un gaz ideal sufera o
transformare politropa ![]() . Sa se calculeze capacitatea termica in aceasta transformare. Se da
constanta universala a gazelor,
. Sa se calculeze capacitatea termica in aceasta transformare. Se da
constanta universala a gazelor, ![]()
Rezolvare Capacitatea termica este de relatia
![]() (P.2.3.1)
(P.2.3.1)
sinand seama de expresia principiului I al termodinamicii
![]() (P.2.3.2)
(P.2.3.2)
se obtine
![]() (P.2.3.3)
(P.2.3.3)
Cu ajutorul ecuatiei
termice de stare a gazului ideal ![]() ecuatia politropei
ecuatia politropei ![]() devine
devine ![]() , de unde
, de unde ![]() , iar
, iar
![]() (P.2.3.4)
(P.2.3.4)
P.2.4. Un gaz perfect sufera un proces cvasistatic reversibil in care presiunea variaza cu volumul dupa legea:
![]() (P.2.4.1)
(P.2.4.1)
unde ![]() si
si ![]() sunt constante pozitive. Sa se
determine: a) relatia dintre presiune si temperatura si b) temperatura maxima.
sunt constante pozitive. Sa se
determine: a) relatia dintre presiune si temperatura si b) temperatura maxima.
Rezolvare a) Relatia dintre presiune si temperatura se obtine eliminand volumul intre ecuatia de stare termica, (care defineste o familie de izoterme (fig. P.2.4.1)):
![]() (P.2.4.2)
(P.2.4.2)
si ecuatia procesului cvasistetic reversibil (P.2.4.1):
![]() , (P.2.4.3)
, (P.2.4.3)
de unde
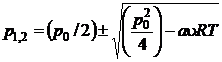 . (P.2.4.4)
. (P.2.4.4)
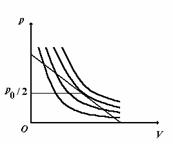
Fig. P.2.4.1. Reprezentarea grafica a familiei de izoterme si a procesului cvasistatic
reversibil pentru care ![]() .
.
b) Temperatura se obtine din relatia (P.2.4.3) sub forma:
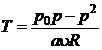 (P.2.4.5)
(P.2.4.5)
Din conditia de extrem
![]() (P.2.4.6)
(P.2.4.6)
se obtine ![]() si valoarea maxima a
temperaturii:
si valoarea maxima a
temperaturii:
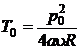 (P.2.4.7)
(P.2.4.7)
Se observa ca pentru ![]() curba procesului cvasistatic este
tangenta la izoterma
curba procesului cvasistatic este
tangenta la izoterma ![]() (fig. P.2.4.1). Pentru
(fig. P.2.4.1). Pentru ![]() , temperatura scade odata cu cresterea presiunii, iar pentru
, temperatura scade odata cu cresterea presiunii, iar pentru ![]() , temperatura scade odata cu micsorarea presiunii.
, temperatura scade odata cu micsorarea presiunii.
P.2.5. Sa se determine expresia coeficientului de variatie a presiunii cu temperatura
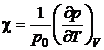 (P.2.5.1)
(P.2.5.1)
in cazul unui gaz Van der Waals descris de ecuatia termica de stare
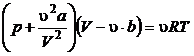 (P.2.5.2)
(P.2.5.2)
unde ![]() si
si ![]() sunt constante.
sunt constante.
Rezolvare Din ecuatia termica de stare (P.2.5.2) se obtine presiunea gazului sub forma:
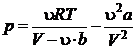 (P.2.5.3)
(P.2.5.3)
sinand seama de relatia de definitie (P.2.5.1) expresia coeficientului de variatie a presiunii cu temperatura este:
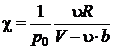 (P.2.5.4)
(P.2.5.4)
unde ![]() este presiunea starii de referinta.
este presiunea starii de referinta.
P.2.6. Sa se stabileasca relatia Mayer pentru gazul real Van der Waals.
Rezolvare sinand seama de relatiile de definitie ale capacitatilor calorice la presiune si volum constant se obtine succesiv:
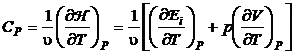
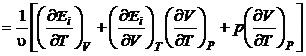 (P.2.6.1)
(P.2.6.1)
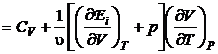
iar
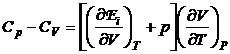 (P.2.6.2)
(P.2.6.2)
Diferentiind ecuatia Van der Waals
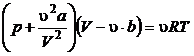 (P.2.6.3)
(P.2.6.3)
la presiune constanta, rezulta:
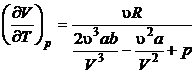 (P.2.6.4)
(P.2.6.4)
sinand seama ca in cazul gazului real Van der Waals
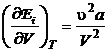 (P.2.6.5)
(P.2.6.5)
si de relatiile (P.2.6.3) si (P.2.6.4) se obtine in final relatia Mayer
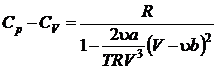 (P.2.6.6)
(P.2.6.6)
In cazul gazului ideal
corectiile ![]() si
si ![]() ale gazului real Van de Waals se pot
neglija, iar relatia Mayer (P.2.6.6) devine
ale gazului real Van de Waals se pot
neglija, iar relatia Mayer (P.2.6.6) devine ![]()
P.2.7. Sa se calculeze variatia
entropiei pentru ![]() moli de gaz biatomic, cand se dilata
de la volumul
moli de gaz biatomic, cand se dilata
de la volumul ![]() la volumul
la volumul ![]() , daca dilatarea se face: a) pe o politropa
, daca dilatarea se face: a) pe o politropa ![]() , b) pe o izoterma. Se cunosc:
, b) pe o izoterma. Se cunosc: ![]() si indicele politropei
si indicele politropei ![]()
Rezolvare a) sinand seama de expresiile variatiei entropiei
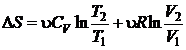 (P.2.7.1)
(P.2.7.1)
si de cea corespunzatoare transformarii politrope
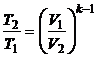 (P.2.7.2)
(P.2.7.2)
se obtine in final
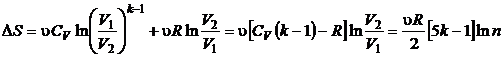 (P.2.7.3)
(P.2.7.3)
unde ![]()
b)
In cazul izotermei, ![]()
![]() , iar de expresia variatiei
, iar de expresia variatiei
entropiei devine:
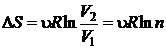 (P.2.7.4)
(P.2.7.4)
P.2.8. Pentru un kmol de gaz perfect, a
carui caldura molara variaza dupa legea ![]() , unde
, unde ![]() si
si ![]() sunt constante, iar
sunt constante, iar ![]() este temperatura, sa se calculeze:
a) energia libera,
este temperatura, sa se calculeze:
a) energia libera, ![]() , b) entalpia libera,
, b) entalpia libera, ![]()
Rezolvare a) Energia libera a unui sistem termodinamic este data de relatia:
![]() (P.2.8.1)
(P.2.8.1)
unde:
![]() (P.2.8.2)
(P.2.8.2)
este energia interna, iar
![]() (P.2.8.3)
(P.2.8.3)
este entropia sistemului.
Din relatiile (P.2.8.2) si (P.2.8.3) se obtine energia libera sub forma:
![]() (P.2.8.4)
(P.2.8.4)
b) Entalpia libera se calculeaza din relatia:
![]() (P.2.8.5)
(P.2.8.5)
P.2.9. Se amesteca o cantite ![]() dintr-un lichid, avand caldura
specifica
dintr-un lichid, avand caldura
specifica ![]() , la temperatura
, la temperatura ![]() , cu o cantitate m2
dintr-un alt lichid, avand caldura specifica
, cu o cantitate m2
dintr-un alt lichid, avand caldura specifica ![]() , la temperatura
, la temperatura ![]() . a) Considerand ca
. a) Considerand ca ![]() sa se calculeze variatia entropiei
pana cand sistemul ajunge in starea de ehilibru termic, stiind ca lichidele nu
reactioneaza chimic intre ele. b) Sa se arate ca
sa se calculeze variatia entropiei
pana cand sistemul ajunge in starea de ehilibru termic, stiind ca lichidele nu
reactioneaza chimic intre ele. b) Sa se arate ca ![]() , pentru cazul particular cand
, pentru cazul particular cand ![]() si
si ![]()
Rezolvare a) Din ecuatia corespunzatoare echilibrului termic
![]() (P.2.9.1)
(P.2.9.1)
se obtine temperatura de echilibru
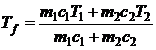 (P.2.9.2)
(P.2.9.2)
Variatia totala a entropiei este data de relatia:
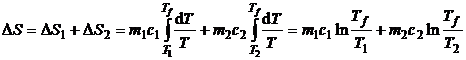
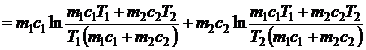 (P.2.9.3)
(P.2.9.3)
b) In cazul particular
![]() (P.2.9.4)
(P.2.9.4)
iar variatia entropiei devine:
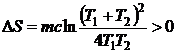 , (P.2.9.5)
, (P.2.9.5)
intrucat
![]() (P.2.9.6)
(P.2.9.6)
P.2.10. Sa se calculeze: a) energia
libera si b) entalpia libera pentru ![]() kmoli de gaz real care satisface
ecuatia Van der Waals.
kmoli de gaz real care satisface
ecuatia Van der Waals.
Rezolvare a) sinand seama de expresiile energiei interne
![]() (P.2.10.1)
(P.2.10.1)
si entropiei
![]() (P.2.10.2)
(P.2.10.2)
se obtine expresia energiei libere sub forma:
![]() (P.2.10.3)
(P.2.10.3)
b) Entalpia libera este data de relatia:
![]() . (P.2.10.4)
. (P.2.10.4)
P.2.11. Ecuatia de stare a radiatiei termice este:
![]() (P.2.11.1)
(P.2.11.1)
unde ![]() este densitatea de energie interna a
radiatiei. Sa se calculeze: a) energia interna si b) entropia corespunzatoare
radiatiei termice.
este densitatea de energie interna a
radiatiei. Sa se calculeze: a) energia interna si b) entropia corespunzatoare
radiatiei termice.
Rezolvare a) Stiind ca in general energia interna ![]() si entropia
si entropia
![]() , prin diferentiere rezulta:
, prin diferentiere rezulta:
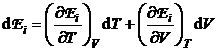 (P.2.11.2)
(P.2.11.2)
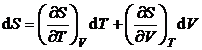 . (P.2.11.3)
. (P.2.11.3)
sinand seama de ecuatia fundamentala a termodinamicii
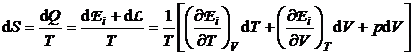 (P.2.11.4)
(P.2.11.4)
in urma identificarii relatiilor (P.2.11.3) si (P.2.11.4), se obtine:
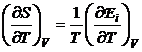 (P.2.11.5)
(P.2.11.5)
si
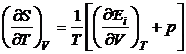 (P.2.11.6)
(P.2.11.6)
Din relatiile (P.2.11.5) si (P.2.11.6), rezulta:
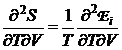 (P.2.11.7)
(P.2.11.7)
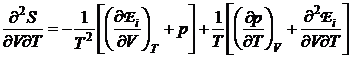 (P.2.11.8)
(P.2.11.8)
sinand seama ca entropia este o functie de stare care are o diferentiala exacta, in urma identificarii relatiilor (P.2.11.7) si (P.2.11.8), se obtine:
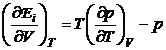 (P.2.11.9)
(P.2.11.9)
Inlocuind ![]() si relatia (P.2.11.2) in
(P.2.11.9), rezulta:
si relatia (P.2.11.2) in
(P.2.11.9), rezulta:
![]() (P.2.11.10)
(P.2.11.10)
In urma urma integrarii ecuatiei (P.2.11.10) se obtine expresia densitatii de energie interna:
![]() (P.2.11.11)
(P.2.11.11)
si respectiv a energiei interne:
![]() (P.2.11.12)
(P.2.11.12)
b) Din relatiile (P.2.11.4) si (P.2.11.12), rezulta:
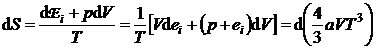 (P.2.11.13)
(P.2.11.13)
si in final dupa integrarea ecuatiei (P.2.11.13), expresia entropiei
![]() (P.2.11.14)
(P.2.11.14)
P.2.12. Considerand ca energia interna a
unei substante paramagnetice ideala depinde numai de temperatura, sa se
calculeze diferenta capacitatilor calorice ![]()
Rezolvare. Din ecuatia termica de
stare, ![]() si ecuatia calorica de stare,
si ecuatia calorica de stare, ![]() , unde
, unde ![]() si
si ![]() sunt parametri externi respectiv fortele
generalizate, relatiile de definitie ale capacitatilor calorice corespunzatoare
acestor parametri se obtin cu ajutorul principiului I al termodinamicii sub
forma:
sunt parametri externi respectiv fortele
generalizate, relatiile de definitie ale capacitatilor calorice corespunzatoare
acestor parametri se obtin cu ajutorul principiului I al termodinamicii sub
forma:
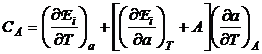
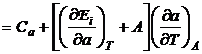 , (P.2.12.1)
, (P.2.12.1)
iar
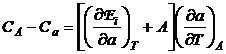 . (P.2.12.2)
. (P.2.12.2)
In cazul unei substante paramagnetice, ![]() si
si ![]() ,
, ![]() fiind intensitatea
campului magnetic iar
fiind intensitatea
campului magnetic iar ![]() magnetizarea, iar relatia
(P.2.12.2) devine:
magnetizarea, iar relatia
(P.2.12.2) devine:
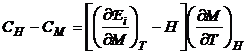 . (P.2.12.3)
. (P.2.12.3)
Din ecuatia termica de stare ![]() si legea Curie
si legea Curie ![]() , unde
, unde ![]() si
si ![]() sunt susceptibilitatea
magnetica si respectiv constanta Curie, rezulta:
sunt susceptibilitatea
magnetica si respectiv constanta Curie, rezulta:
![]() . (P.2.12.4)
. (P.2.12.4)
Intrucat pentru o substanta paramagnetica ideala 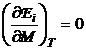 din relatiile
(P.2.12.3) si (P.2.12.4) se obtine in final:
din relatiile
(P.2.12.3) si (P.2.12.4) se obtine in final:
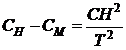 . (P.2.12.5)
. (P.2.12.5)
P.2.13. Sa
se calculeze randamentul unei masini termice care functioneaza cu un gaz
perfect dupa ciclul reprezentat in fig. P.2.13.1, cand transformarile BC si DA
sunt adiabatice. Se cunosc: ![]() si
si 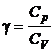 , iar caldurile molare in transformarile AB si CD sunt egale
cu
, iar caldurile molare in transformarile AB si CD sunt egale
cu ![]() .
.
Rezolvare Randamentul masinii termice este dat de relatia:
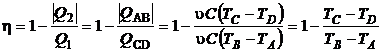 (P.2.13.1)
(P.2.13.1)
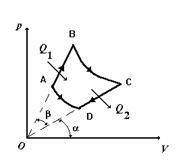
Fig. P.2.13.1. Ciclul parcurs de masina termica.
Din ecuatiile transformarilor adiabatice:
![]()
![]() , (P.2.13.2)
, (P.2.13.2)
si respectiv ale transformarilor AB si CD:
![]()
![]() (P.2.13.3)
(P.2.13.3)
![]()
![]() (P.2.13.4)
(P.2.13.4)
se obtin relatiile:
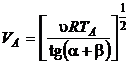
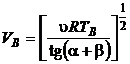 (P.2.13.5)
(P.2.13.5)
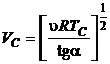
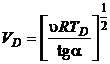 (P.2.13.6)
(P.2.13.6)
Eliminand volumele intre relatiile (P.2.13.2), (P.2.13.5) si (P.2.13.6), rezulta:
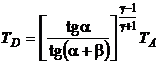
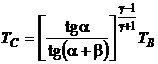 (P.2.13.7)
(P.2.13.7)
Inlocuind temperaturile date de relatia (P.2.13.7) in expresia randamentului (P.2.13.1), se obtine in final:
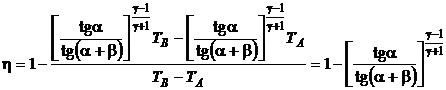 (P.2.13.8)
(P.2.13.8)
P.2.14. Sa se evalueze caldurile latente
in cazul cand ![]()
Rezolvare Din definitia caldurilor latente si respectiv a
entropiei ![]() , rezulta:
, rezulta:
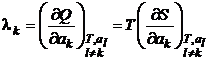 (P.2.14.1)
(P.2.14.1)
sinand seama de expresia diferentialei energiei libere:
![]() (P.2.14.2)
(P.2.14.2)
din conditia de integrabilitate se obtine:
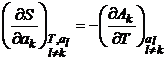 (P.2.14.3)
(P.2.14.3)
Inlocuind relatia (P.2.14.3) in (P.2.14.1) si trecand la limita, rezulta:
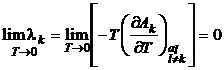 . (P.2.14.4)
. (P.2.14.4)
P.2.15. Sa
se evalueze fortele generalizate si coordonatele generalizate in cazul cand ![]() .
.
Rezolvare Coeficientul termodinamic, asociat coordonatei ![]() este date de relatia:
este date de relatia:
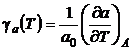 , (P.2.15.1)
, (P.2.15.1)
unde ![]() este valoarea de
referinta a acestei coordonate, iar
este valoarea de
referinta a acestei coordonate, iar ![]() este forta generalizata
conjugata lui
este forta generalizata
conjugata lui ![]() . sinand seama de expresia diferentialei entalpiei libere:
. sinand seama de expresia diferentialei entalpiei libere:
![]() , (P.2.15.2)
, (P.2.15.2)
din conditia de integrabilitate se obtine:
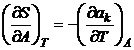 (P.2.15.3)
(P.2.15.3)
iar
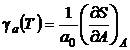 (P.2.15.4)
(P.2.15.4)
In cazul cand ![]()
![]() , iar
, iar
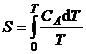 . (P.2.15.5)
. (P.2.15.5)
si
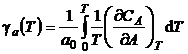 . (P.2.15.6)
. (P.2.15.6)
Din expresia diferentialei entropiei ![]() , a principiului I al termodinamicii si din conditia
, a principiului I al termodinamicii si din conditia 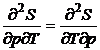 , rezulta:
, rezulta:
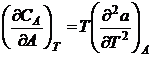 . (P.2.15.7)
. (P.2.15.7)
Inlocuind relatia (P.2.15.7) in (P.2.15.6), se obtine succesiv:
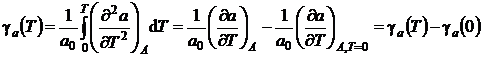 (P.2.15.8)
(P.2.15.8)
si deci ![]() pentru
pentru ![]() , iar
, iar ![]() devine independent de temperatura.
devine independent de temperatura.
P.3.1. Se considera un oscilator armonic liniar care oscileaza dupa legea:
![]() . (P.3.1.1)
. (P.3.1.1)
a) Sa se deduca ecuatia traiectoriei in spatiul fazelor. b) Sa se verifice prin calcul direct teorema de conservare a volumului in spatiul fazelor in timpul miscarii.
Rezolvare a) Impulsul particulei este dat de relatia:
![]() (P.3.1.2)
(P.3.1.2)
Eliminand timpul intre ecuatiile (P.3.1.1) si (P.3.1.2) se obtine ecuatia traiectoriei in spatiul fazelor:
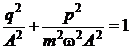 , (P.3.1.3)
, (P.3.1.3)
aceasta reprezentand o elipsa.
b) Pentru a demonstra prin calcul direct teorema de conservare a volumului in spatiul fazelor in timpul miscarii trebuie verificata relatia
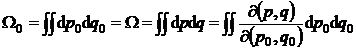 (P.3.1.4)
(P.3.1.4)
unde 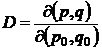 este determinantul (jacobianul)
corespunzator transformarii.
este determinantul (jacobianul)
corespunzator transformarii.
La momentul initial ![]()
![]() (P.3.1.5)
(P.3.1.5)
![]() (P.3.1.6)
(P.3.1.6)
Eliminand variabila ![]() intre ecuatiile (P.3.1.1),
(P.3.1.2), (P.3.1.5) si (P.3.1.6), rezulta:
intre ecuatiile (P.3.1.1),
(P.3.1.2), (P.3.1.5) si (P.3.1.6), rezulta:
![]() (P.3.1.7)
(P.3.1.7)
![]() (P.3.1.8)
(P.3.1.8)
sinand seama de relatiile (P.3.1.5) si (P.3.1.6) determinantul corespunzator transformarii devine:
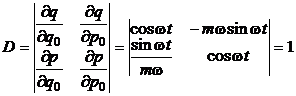 (P.3.1.9)
(P.3.1.9)
iar relatia (P.3.1.4) este verificata.
P.3.2. Probabilitatea ![]() ca variabilele
ca variabilele ![]() si
si ![]() sa ia valori cuprinse in intervalele
sa ia valori cuprinse in intervalele
![]() si
si ![]() este:
este:
![]() (P.3.2.1)
(P.3.2.1)
Sa se determine a) constanta de normare si b) expresiile valorilor medii ![]() si
si ![]() , stiind ca variabilele
, stiind ca variabilele ![]() si
si ![]() iau valori cuprinse in intervalul
iau valori cuprinse in intervalul ![]()
Rezolvare a) Constanta ![]() se calculeaza din conditia de
normare:
se calculeaza din conditia de
normare:
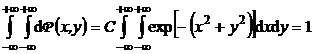 (P.3.2.2)
(P.3.2.2)
Intrucat
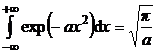 (P.3.2.3)
(P.3.2.3)
din relatia (P.3.2.2) rezulta ![]()
b) Pe baza proprietatilor probabilitatilor
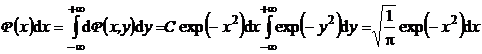 , (P.3.2.4)
, (P.3.2.4)
iar valoarea medie a variabilei ![]() este:
este:
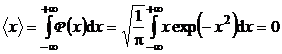 . (P.3.2.5)
. (P.3.2.5)
In mod analog se obtine ![]() .
.
P.3.3. Se considera doua recipiente izolate care contin doua gaze ideale
monoatomice identice avand aceeasi temperatura, ![]() si acelasi numar,
si acelasi numar, ![]() de particule aflate la
presiuni diferite
de particule aflate la
presiuni diferite ![]() si
si ![]() . In urma punerii in contact a recipientelor sa se calculeze:
a) presiunea finala,
. In urma punerii in contact a recipientelor sa se calculeze:
a) presiunea finala, ![]() si b) variatia
corespunzatoare a entropiei,
si b) variatia
corespunzatoare a entropiei, ![]() .
.
Rezolvare a) sinand seama de ecuatia de stare a gazului ideal
![]() , (P.3.3.1)
, (P.3.3.1)
unde ![]() si
si ![]() , rezulta:
, rezulta:
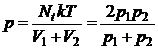 (P.3.3.2)
(P.3.3.2)
b) Variatia entropiei este data de relatia:
![]()
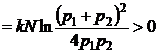 (P.3.3.3)
(P.3.3.3)
P.3.4. Sa se calculeze procentul de molecule ale caror viteze sunt cuprinse intre viteza cea mai probabila si viteza patratica medie.
Rezolvare Procentul de molecule ale caror viteze sunt cuprinse intre viteza cea mai probabila si viteza patratica medie se obtine prin integrarea functiei de distributie a vitezelor Maxwell:
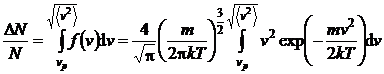 (P.3.4.1)
(P.3.4.1)
Notand cu
![]() unde
unde 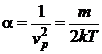 (P.3.4.2)
(P.3.4.2)
relatia (P.3.4.1) devine:
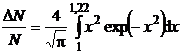
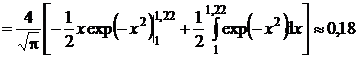 . (P.3.4.3)
. (P.3.4.3)
P.3.5. Sa se
afle raportul, ![]() dintre numarul de
molecule cu vitezele cuprinse in intervalul
dintre numarul de
molecule cu vitezele cuprinse in intervalul ![]() si numarul de molecule
cu vitezele cuprinse in intervalul
si numarul de molecule
cu vitezele cuprinse in intervalul ![]() , unde
, unde ![]() si
si ![]() reprezinta viteza cea
mai probabila si respectiv viteza patratica medie.
reprezinta viteza cea
mai probabila si respectiv viteza patratica medie.
Rezolvare sinand seama de functia de distributie a vitezelor Maxwell:
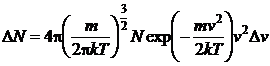 , (P.3.5.1)
, (P.3.5.1)
rezulta:
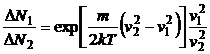 , (P.3.5.2)
, (P.3.5.2)
unde
![]() si
si ![]() . (P.3.5.3)
. (P.3.5.3)
Inlocuind relatia (P.3.15.3) in (P.3.15.2), se obtine:
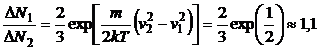 . (P.3.5.4)
. (P.3.5.4)
P.3.6. Cunoscand expresia functiei de distributie a vitezelor Maxwell
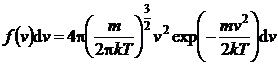 , (P.3.6.1)
, (P.3.6.1)
sa se calculeze: a) functia
de distributie in raport cu energia cinetica a unei molecule, ![]() si b) energia cinetica
de translatie cea mai probabila,
si b) energia cinetica
de translatie cea mai probabila, ![]() a moleculelor unui gaz
ideal.
a moleculelor unui gaz
ideal.
Rezolvare a) Din expresia energiei cinetice, rezulta:
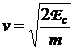 si
si 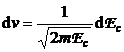 (P.3.6.2)
(P.3.6.2)
Inlocuind relatia (P.3.6.2) in (P.3.6.1), se obtine:
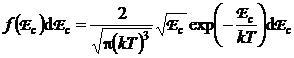 , (P.3.6.3)
, (P.3.6.3)
care reprezinta
probabilitatea ca energia cinetica a unei molecule sa fie cuprinsa in
intervalul ![]() .
.
b) Anuland derivata functiei ![]() in raport cu
in raport cu ![]() , rezulta:
, rezulta:
![]() (P.3.6.4)
(P.3.6.4)
care nu corespunde vitezei celei mai probabile 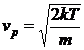
P.3.7. Sa se calculeze a) masa coloanei
de aer din atmosfera Pamantului avand sectiunea ![]() si inaltimea
si inaltimea ![]() si b) greutatea acesteia la inaltime
infinita. Se considera ca temperatura
si b) greutatea acesteia la inaltime
infinita. Se considera ca temperatura ![]() , acceleratia gravitationala
, acceleratia gravitationala ![]() si ca acestea nu variaza cu inaltimea.
Se cunoaste:
si ca acestea nu variaza cu inaltimea.
Se cunoaste: ![]() si
si ![]()
Rezolvare a) Masa de aer cuprinsa intre cotele ![]() este:
este:
![]() (P.3.7.1)
(P.3.7.1)
unde densitatea ![]() a gazului variaza cu inaltimea dupa
legea (P.3.17.4):
a gazului variaza cu inaltimea dupa
legea (P.3.17.4):
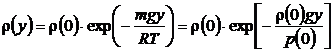 (P.3.7.2)
(P.3.7.2)
![]() fiind densitatea la suprafata Pamantului.
fiind densitatea la suprafata Pamantului.
sinand seama de relatiile (P.3.7.1) si (P.3.7.2) masa totala a coloanei de aer este data de relatia:
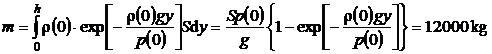 . (P.3.7.3)
. (P.3.7.3)
b) In cazul cand ![]() masa totala de aer din relatia (P.3.7.3)
devine
masa totala de aer din relatia (P.3.7.3)
devine ![]() , iar greutatea acesteia
, iar greutatea acesteia
![]() . (P.3.7.4)
. (P.3.7.4)
P.3.8. Sa se calculeze a) raportul
concentratiilor hidrogenului ![]() fata de bioxidul de carbon
fata de bioxidul de carbon ![]() functie de inaltime si b) inaltimea
la care acest raport se tripleaza presupunand ca la nivelul solului cele doua
gaze au aceleasi concentratii.
functie de inaltime si b) inaltimea
la care acest raport se tripleaza presupunand ca la nivelul solului cele doua
gaze au aceleasi concentratii.
Se considera ca temperatura ![]() , acceleratia gravitationala
, acceleratia gravitationala ![]() si ca acestea nu variaza cu inaltimea.
Se cunoaste:
si ca acestea nu variaza cu inaltimea.
Se cunoaste: ![]()
Rezolvare Concentratiile celor doua gaze variaza cu inaltimea dupa legea:
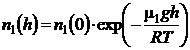 si
si 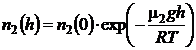 (P.3.8.1)
(P.3.8.1)
Raportul concentratiilor hidrogenului fata de bioxidul de carbon functie de inaltime este dat de relatia:
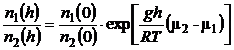 (P.3.8.2)
(P.3.8.2)
b) Inaltimea la care raportul dat de relatia (P.3.18.2) se dubleaza este:
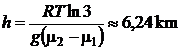 (P.3.8.3)
(P.3.8.3)
P.4.1. Stiind ca intensitatea campului
electric al Pamantului, ![]() scade liniar de la suprafata
acestuia, unde are valoarea
scade liniar de la suprafata
acestuia, unde are valoarea ![]() , pana la inaltimea
, pana la inaltimea ![]() , unde are valoarea
, unde are valoarea 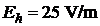 , sa se calculeze densitatea volumica medie a sarcinii electrice,
, sa se calculeze densitatea volumica medie a sarcinii electrice, ![]() din atmosfera. Se da:
din atmosfera. Se da: ![]()
![]() (P.4.1.1)
(P.4.1.1)
si punand conditiile la limita: ![]() si
si ![]() , se obtine
, se obtine ![]() , iar in final:
, iar in final:
![]() . (P.4.1.2)
. (P.4.1.2)
Aplicand legea inductiei electrice:
![]() (P.4.1.3)
(P.4.1.3)
rezulta:
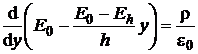 (P.4.1.4)
(P.4.1.4)
iar
![]() (P.4.1.5)
(P.4.1.5)
P.4.2. Se considera un potential vector dat de relatia:
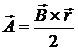 (P.4.2.1)
(P.4.2.1)
unde ![]() este inductia magnetica corespunzatoare
unui camp magnetic uniform, iar
este inductia magnetica corespunzatoare
unui camp magnetic uniform, iar ![]() este vectorul de pozitie. Sa se
verifice ca un camp magnetic uniform,
este vectorul de pozitie. Sa se
verifice ca un camp magnetic uniform, ![]() admite potentialul vector dat de
relatia (P.4.2.1).
admite potentialul vector dat de
relatia (P.4.2.1).
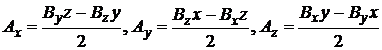 (P.4.2.2)
(P.4.2.2)
Relatia dintre inductia
campului magnetic, ![]() si potentialul vector,
si potentialul vector, ![]() corespunzator este:
corespunzator este:
![]() (P.4.2.3)
(P.4.2.3)
sinand seama de relatiile (P.4.2.2) si (P.4.2.3), rezulta verificare ceruta in enuntul problemei:
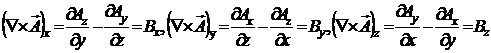 (P.4.2.4)
(P.4.2.4)
P.4.3. Pe armaturile unui condensator
plan de forma circulara cu razele egale, situate la distanta ![]() (fig. P.4.3.1) se aplica o tensiune
alternativa
(fig. P.4.3.1) se aplica o tensiune
alternativa
![]() (P.4.3.1)
(P.4.3.1)
Sa se calculeze intensitatea campului magnetic, ![]() intr-un punct O situat intre armaturile
condensatorului la distanta
intr-un punct O situat intre armaturile
condensatorului la distanta ![]() de axul acestuia.
de axul acestuia.
![]() . (P.4.3.2)
. (P.4.3.2)
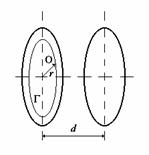
Fig. P.4.3.1. Reprezentarea condensatorului plan de forma circulara.
Aplicand legea circuitului magnetic sub forma:
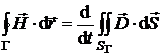 (P.4.3.3)
(P.4.3.3)
unde ![]() reprezinta conturul care trece prin
punctul O, iar
reprezinta conturul care trece prin
punctul O, iar ![]() este suprafata cercului marginit de
contur, rezulta:
este suprafata cercului marginit de
contur, rezulta:
![]() (P.4.3.4)
(P.4.3.4)
Din relatiile (P.4.3.2) si (P.4.3.4), se obtine:
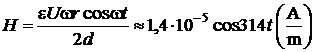 (P.4.3.5)
(P.4.3.5)
P.4.4. Se considera un conductor liniar
infinit parcurs de un curent electric cu intensitatea ![]() situat in vid in acelasi plan cu un
cadru dreptunghiular avand laturile
situat in vid in acelasi plan cu un
cadru dreptunghiular avand laturile ![]() si
si ![]() la distanta
la distanta ![]() fata de latura
fata de latura ![]() (fig. P.4.4.1). Sa se calculeze:
fluxul,
(fig. P.4.4.1). Sa se calculeze:
fluxul, ![]() al inductiei magnetice prin cadru si
b) tensiunea electromotoare,
al inductiei magnetice prin cadru si
b) tensiunea electromotoare, ![]() indusa in cadru daca intensitatea
curentilui scade cu viteza
indusa in cadru daca intensitatea
curentilui scade cu viteza ![]()
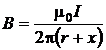 ,
(P.4.4.1)
,
(P.4.4.1)
iar fluxul elementar care il strabate se scrie sub forma:
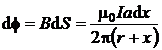 . (P.4.4.2)
. (P.4.4.2)
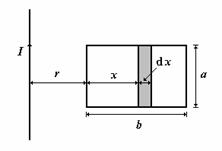
Fig. P.4.4.1. Reprezentarea conductorului si a cadrului dreptunghiular.
sinand seama de relatia (P.4.4.2) fluxul total este:
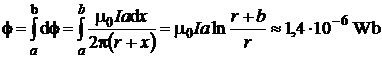 . (P.4.4.3)
. (P.4.4.3)
b) Tensiunea electromotoare indusa in cadru se calculeaza cu ajutorul relatiei:
![]() . (P.4.4.4)
. (P.4.4.4)
P.4.5. Se
considera doua medii, 1 si 2 caracterizate de urmatorii parametri constanti: ![]() ,
, ![]() si respectiv
si respectiv ![]() ,
, ![]() , acestea fiind separate de o suprafata plana plasata in
, acestea fiind separate de o suprafata plana plasata in ![]() (fig. P.4.5.1). In
mediul 1 densitatea de curent este
(fig. P.4.5.1). In
mediul 1 densitatea de curent este ![]() , unde
, unde ![]() Considerand ca in
ambele medii campurile sunt uniforme spatial si independente de timp, sa se
calculeze: a) densitatea de curent in mediul 2,
Considerand ca in
ambele medii campurile sunt uniforme spatial si independente de timp, sa se
calculeze: a) densitatea de curent in mediul 2, ![]() si b) densitatea
superficiala de sarcina,
si b) densitatea
superficiala de sarcina, ![]() in planul
in planul ![]() .
.
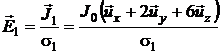 . (P.4.5.1)
. (P.4.5.1)
sinand seama de conditia la limita pentru
componentele tangentiale ale intensitatii campului electric, ![]() , rezulta:
, rezulta:
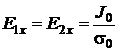 , si
, si 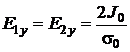 (P.4.5.2)
(P.4.5.2)
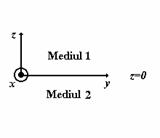
Fig. P.4.5.1. Reprezentarea mediilor 1 si 2.
Pe baza conditiei la limita pentru densitatea de curent
![]() (P.4.5.3)
(P.4.5.3)
unde s-a tinut seama ca in ambele medii campurile sunt uniforme spatial ![]() , independente de timp
, independente de timp 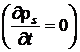 , rezulta:
, rezulta:
![]() (P.4.5.4)
(P.4.5.4)
iar densitatea de curent in mediul 2, devine:
![]() (P.4.5.5)
(P.4.5.5)
b) sinand seama de relatiile (P.4.5.2), (P.4.5.4) si de conditia la limita pentru componentele normale ale inductiei electrice,
![]() , sau in cazul de mai sus
, sau in cazul de mai sus ![]() (P.4.5.6)
(P.4.5.6)
unde ![]() , rezulta:
, rezulta:
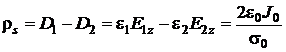 (P.4.5.7)
(P.4.5.7)
P.4.6. Se considera o unda electromagnetica plana
![]() (P.4.6.1)
(P.4.6.1)
unde ![]() si
si ![]()
![]() si
si ![]() fiind versorii axelor
fiind versorii axelor ![]() si
si ![]() ), care se propaga in vid. Sa se calculeze vectorul intensitate camp
magnetic,
), care se propaga in vid. Sa se calculeze vectorul intensitate camp
magnetic, ![]() in punctul determinat de vectorul de
pozitie
in punctul determinat de vectorul de
pozitie ![]() la momentul de timp
la momentul de timp ![]()
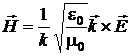 (P.4.6.2)
(P.4.6.2)
in cazul considerat mai sus, se obtine:
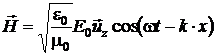 (P.4.6.3)
(P.4.6.3)
unde ![]() este versorul axei
este versorul axei ![]() La
momentul
La
momentul ![]() , rezulta:
, rezulta:
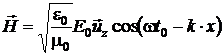 (P.4.6.4)
(P.4.6.4)
Distanta ![]() este parcursa de unda care se
deplaseaza cu viteza
este parcursa de unda care se
deplaseaza cu viteza 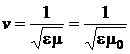 in:
in:
![]() (P.4.6.5)
(P.4.6.5)
iar timpul total necesar parcurgerii lamei devine:
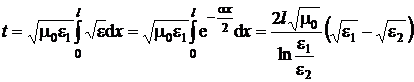 (P.4.6.6)
(P.4.6.6)
P.4.7. Sa se calculeze componenta
vectorului inductie magnetica, ![]() a unei unde electromagnetice stationara
cu
a unei unde electromagnetice stationara
cu
![]() (P.4.7.1)
(P.4.7.1)
care se afla in vid de-a lungul axi ![]()
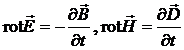 (P.4.7.2)
(P.4.7.2)
se obtine succesiv:
![]() (P.4.7.3)
(P.4.7.3)
In urma inlocuirii relatiei (P.4.7.1) in (P.4.7.2) si (P.4.7.3), rezulta:
![]() , (P.4.7.4)
, (P.4.7.4)
iar in final:
![]() ,
(P.4.7.5)
,
(P.4.7.5)
unde ![]() si
si ![]() .
.
P.4.8. Sa se
calculeze valoarea medie a vectorului Poynting, ![]() in cazul unei unde
electromagnetice stationara
in cazul unei unde
electromagnetice stationara
![]() (P.4.8.1)
(P.4.8.1)
care se propaga in vid.
![]() (P.4.8.2)
(P.4.8.2)
unde ![]() sinand seama ca
sinand seama ca
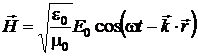 , (P.4.8.3)
, (P.4.8.3)
rezulta:
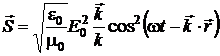 (P.4.8.4)
(P.4.8.4)
Valoarea medie a vectorului Poynting este data de relatia:
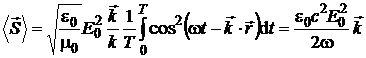 (P.4.8.5)
(P.4.8.5)
P.4.9. Intr-un dispozitiv Young, distanta
dintre cele doua orificii, ![]() este
este ![]() , iar ecranul, E pe care se observa franjele de interferenta este plasat la
distanta
, iar ecranul, E pe care se observa franjele de interferenta este plasat la
distanta ![]() de planul orificiilor (fig.
P.4.9.1). Sa se calculeze: a) lungimea de unda,
de planul orificiilor (fig.
P.4.9.1). Sa se calculeze: a) lungimea de unda, ![]() a radiatiei utilizate stiind ca
interfranja este
a radiatiei utilizate stiind ca
interfranja este ![]() si b) grosimea
si b) grosimea ![]() a unei lame de sticla cu fete plan
paralele care introdusa in drumul uneia dintre unde produce deplasarea franjei
centrale in pozitia celei de-a 20-a franje luminoasa.
a unei lame de sticla cu fete plan
paralele care introdusa in drumul uneia dintre unde produce deplasarea franjei
centrale in pozitia celei de-a 20-a franje luminoasa.
![]() (P.4.9.1)
(P.4.9.1)
rezulta interfranja:
![]() (P.4.9.2)
(P.4.9.2)
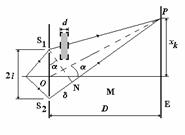
Fig. P.4.9.1. Dispozitivul Young
b) Grosimea ![]() a unei lame de sticla cu fete plan
paralele care introdusa in drumul uneia dintre unde produce deplasarea franjei
centrale in pozitia celei de-a 20-a franje luminoasa se calculeaza din relatia:
a unei lame de sticla cu fete plan
paralele care introdusa in drumul uneia dintre unde produce deplasarea franjei
centrale in pozitia celei de-a 20-a franje luminoasa se calculeaza din relatia:
![]() , sub forma:
, sub forma:
![]() (P.4.9.3)
(P.4.9.3)
P.4.10. Sa se calculeze: a) intensitatea
totala in cazul interferentei a ![]() fascicule luminoase coerente de
acceeasi amplitudine,
fascicule luminoase coerente de
acceeasi amplitudine, ![]() daca intre doua fascicule vecine
exista o diferenta de faza constanta,
daca intre doua fascicule vecine
exista o diferenta de faza constanta, ![]() si b) pentru ce valori ale lui
si b) pentru ce valori ale lui ![]() se obtin maxime si minime de
interferenta.
se obtin maxime si minime de
interferenta.
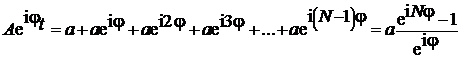 (P.4.10.1)
(P.4.10.1)
Intensitatea luminii este data de relatia:
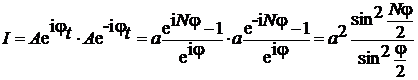 (P.4.10.2)
(P.4.10.2)
b) Intensitatea luminoasa, ![]() are valoare maxima daca
se anuleaza numitorul, adica pentru:
are valoare maxima daca
se anuleaza numitorul, adica pentru: ![]() ,, iar valori minime daca se anuleaza numaratorul, adica
pentru:
,, iar valori minime daca se anuleaza numaratorul, adica
pentru: ![]() . Maximele secundare se obtin in urma anularii derivatei functiei
(P.4.10.2) in raport cu
. Maximele secundare se obtin in urma anularii derivatei functiei
(P.4.10.2) in raport cu ![]() , rezultand ecuatia transcedenta:
, rezultand ecuatia transcedenta:
![]() , (P.4.10.3)
, (P.4.10.3)
care rezolvata conduce la:
![]() (P.4.10.4)
(P.4.10.4)
Scriind numaratorul relatiei (P.4.15.2) succesiv sub forma:
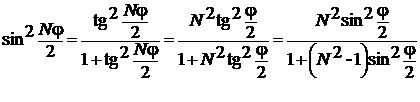 (P.4.10.5)
(P.4.10.5)
valoarea maxima a intensitatii devine:
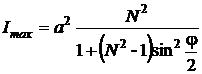 (P.4.10.6)
(P.4.10.6)
In cazul maximului
principal corespunzator valorii ![]() , rezulta:
, rezulta: ![]()
P.4.11. O retea de difractie este iluminata cu o radiatie avand lungimea de unda
![]() si directie
perpendiculara pe aceasta. Doua maxime principale vecine se obtin pentru:
si directie
perpendiculara pe aceasta. Doua maxime principale vecine se obtin pentru: ![]() si
si ![]() . Sa se calculeze: a) constanta,
. Sa se calculeze: a) constanta, ![]() a retelei si b) ordinul maxim,
a retelei si b) ordinul maxim, ![]() al spectrului.
al spectrului.
![]()
![]() (P.4.11.1)
(P.4.11.1)
de unde rezulta: 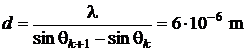
b) Daca in relatia de
calcul a maximelor de difractie (P.4.16.1) se pune conditia ca ![]() , se obtine:
, se obtine:
![]() . (P.4.11.2)
. (P.4.11.2)
P.5.1. Se considera o incinta cu
volumul ![]() cm
cm![]() care contine radiatie termica la temperatura
care contine radiatie termica la temperatura ![]() K. Sa se calculeze: a) capacitatea
calorica la volum constant; b) presiunea radiatiei din incinta. Se dau: constanta
Stefan-Boltzmann,
K. Sa se calculeze: a) capacitatea
calorica la volum constant; b) presiunea radiatiei din incinta. Se dau: constanta
Stefan-Boltzmann, ![]() si viteza luminii
si viteza luminii ![]() m/s.
m/s.
Rezolvare a) Intrucat
![]() unde
unde ![]() (P.5.1.1)
(P.5.1.1)
rezulta
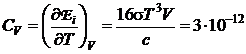 J/K. (P.5.1.2)
J/K. (P.5.1.2)
b) 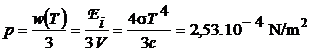 . (P.5.1.3)
. (P.5.1.3)
P.5.2. Intr-o cavitate de volum ![]() , care contine radiatie termica temperatura variaza de la
, care contine radiatie termica temperatura variaza de la ![]() la
la ![]() . Sa se calculeze variatia entropiei radiatiei termice de echilibru din
cavitate. Se dau: constanta Stefan-Boltzmann,
. Sa se calculeze variatia entropiei radiatiei termice de echilibru din
cavitate. Se dau: constanta Stefan-Boltzmann, ![]() si viteza luminii
si viteza luminii ![]() m/s.
m/s.
Rezolvare sinand seama de relatia entropiei :
![]() (P.5.2.1)
(P.5.2.1)
si a densitatii totale de energie radianta
![]() (P.5.2.2)
(P.5.2.2)
se obtine in final
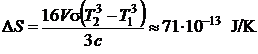 (P.5.2.3)
(P.5.2.3)
P.5.3. Suprafata unui anumit metal este
iluminata succesiv cu radiatii avand lungimile de unda ![]() si
si ![]()
![]() . Stiind ca tensiunile de franare corespunzatoare fotoelectronilor emisi
sunt
. Stiind ca tensiunile de franare corespunzatoare fotoelectronilor emisi
sunt ![]() si respectiv
si respectiv ![]() , de
, de ![]() ori mai mica dacat
ori mai mica dacat ![]() , sa se calculeze: a) constanta Planck si b) lucrul de extractie.
, sa se calculeze: a) constanta Planck si b) lucrul de extractie.
Rezolvare Din bilantul energetic
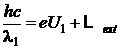
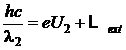 (P.5.3.1)
(P.5.3.1)
si relatia dintre tensiunile de franare
![]() (P.5.3.2)
(P.5.3.2)
se obtine in final
a) 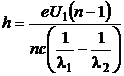 (P.5.3.3)
(P.5.3.3)
b) 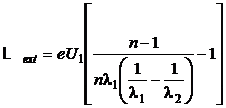 (P.5.3.4)
(P.5.3.4)
P.5.4. Un fascicul de fotoni X cu
lungimea de unda initiala ![]() este difuzat prin efect Compton pe
un electron cvasiliber. Stiind ca unghiul de difuzie al fotonului este
este difuzat prin efect Compton pe
un electron cvasiliber. Stiind ca unghiul de difuzie al fotonului este ![]() sa se calculeze: a) variatia
lungimii de unda a radiatiei, b) unghiul
sa se calculeze: a) variatia
lungimii de unda a radiatiei, b) unghiul ![]() pe care il face electronul de recul
cu directia fotonului incident si c) energia fotonului difuzat. Se dau: viteza
luminii
pe care il face electronul de recul
cu directia fotonului incident si c) energia fotonului difuzat. Se dau: viteza
luminii ![]() m/s, constanta Planck
m/s, constanta Planck ![]() si masa electronului
si masa electronului ![]() kg.
kg.
Rezolvare a) Din relatia
![]() . (P.5.4.1)
. (P.5.4.1)
se obtine pentru variatia lungimii de unda a radiatiei
![]()
![]() (P.5.4.2)
(P.5.4.2)
b) sinand cont ca inainte de difuzie electronul
este practic in repaus, legea de conservare a impulsului (pe directia
impulsului fotonului incident ![]() si pe o directie perpendiculara
si pe o directie perpendiculara ![]() ) se scriu sub forma (fig. P.5.4.1):
) se scriu sub forma (fig. P.5.4.1):
![]() (P.5.4.3)
(P.5.4.3)
![]() . (P.5.4.4)
. (P.5.4.4)
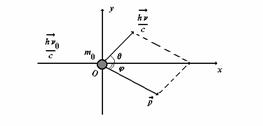
Fig. P.5.4.1. Diagrama impulsurilor.
Impartind relatiile (P.5.4.3) si (P.5.4.4) si tinand seama de (P.5.4.1) se obtine:
 (P.5.4.5)
(P.5.4.5)
de unde
![]() (P.5.4.6)
(P.5.4.6)
c) energia fotonului difuzat este:
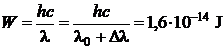 (P.5.4.7)
(P.5.4.7)
P.5.5. Se considera un atom cu doi
electroni al carui nucleu are sarcina ![]() . Utilizand relatia de incertitudine Heisenberg sa se evalueze energia starii
fundamentale. Se dau: masa electronului
. Utilizand relatia de incertitudine Heisenberg sa se evalueze energia starii
fundamentale. Se dau: masa electronului ![]() = 9,1 kg, constanta Planck
normalizata
= 9,1 kg, constanta Planck
normalizata ![]() , sarcina electrica elementara
, sarcina electrica elementara ![]() si permitivitatea electrica
absoluta a vidului
si permitivitatea electrica
absoluta a vidului ![]()
![]()
Rezolvare Considerand ca electronii se afla in pozitii simetrice fata
de nucleu la distanta ![]() si facand aproximatiile
si facand aproximatiile
![]() si
si ![]() (P.5.5.1)
(P.5.5.1)
in relatia de incertitudine Heisenberg
![]() (P.5.5.2)
(P.5.5.2)
energia totala se scrie sub forma:
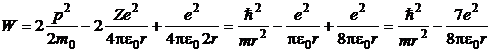 (P.5.5.3)
(P.5.5.3)
Din conditia de minim a
energiei totale ![]() , rezulta:
, rezulta:
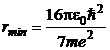 si respectiv
si respectiv 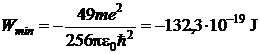 (P.5.5.4)
(P.5.5.4)
P.5.6. Pe baza teoriei Bohr
pentru atomul de hidrogen sa se deduca raportul dintre frecventa de rotatie ![]() a electronului pe orbita
a electronului pe orbita ![]() si frecventa liniei corespunzatoare
excitarii atomului de pe nivelul fundamental pe nivelul
si frecventa liniei corespunzatoare
excitarii atomului de pe nivelul fundamental pe nivelul ![]()
Rezolvare Din formulele frecventei
de rotatie a electronului pe orbita ![]()
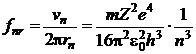 (P.5.6.1)
(P.5.6.1)
si respectiv a frecventei liniei corespunzatoare
excitarii atomului de pe nivelul fundamental pe nivelul ![]()
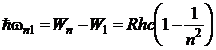 (P.5.6.2)
(P.5.6.2)
se obtine raportul sub forma:
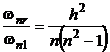 (P.5.6.3)
(P.5.6.3)
P.5.7. Sa se determine functia
proprie corespunzatoare operatorului 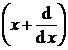
Rezolvare Ecuatia cu valori proprii este de forma:
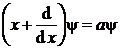 (P.5.7.1)
(P.5.7.1)
In urma separarii variabilelor din ecuatia (P.5.7.1) si integrarii se obtine
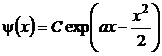 (P.5.7.2)
(P.5.7.2)
P.5.8. Se considera ca la momentul initial starea unei particule cuantice libere este descrisa de functia de unda
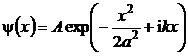 (P.5.8.1)
(P.5.8.1)
unde ![]() si
si ![]() sunt constante. Sa se
calculeze: a) constanta de normare
sunt constante. Sa se
calculeze: a) constanta de normare ![]() si b) densitatea curentului de
probabilitate.
si b) densitatea curentului de
probabilitate.
Se da: 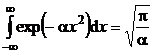 (P.5.8.2)
(P.5.8.2)
Rezolvare a) Din conditia de normare
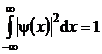 (P.5.8.3)
(P.5.8.3)
si tinand seama de valoarea integralei (P.5.8.2), rezulta
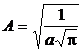 (P.5.8.4)
(P.5.8.4)
b) Inlocuind expresia functiei de unda (P.5.8.1) in formula densitatii curentului de probabilitate se obtine succesiv:
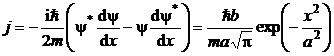 (P.5.8.5)
(P.5.8.5)
P.5.9. Considerand ca la momentul initial starea unei particule cuantice libere este descrisa de functia de unda
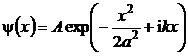 (P.5.9.1)
(P.5.9.1)
unde ![]() si
si ![]() sunt constante, sa se
demonstreze relatia de incertitudine Heisenberg
sunt constante, sa se
demonstreze relatia de incertitudine Heisenberg
![]() (P.5.9.2)
(P.5.9.2)
Se da:
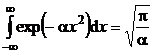 (P.5.9.3)
(P.5.9.3)
Rezolvare Din conditia de normare
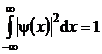 (P.5.9.4)
(P.5.9.4)
si tinand seama de valoarea integralei (P.5.9.3), rezulta
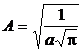 (P.5.9.5)
(P.5.9.5)
Impreciziile
![]() si
si ![]() sunt definite de relatiile:
sunt definite de relatiile:
![]() (P.5.9.6)
(P.5.9.6)
![]() (P.5.9.7)
(P.5.9.7)
Explicitand relatiile (P.5.9.6) si (P.5.9.7) se obtine succesiv
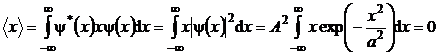 (P.5.9.8)
(P.5.9.8)
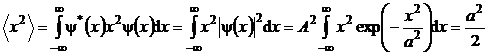 (P.5.9.9)
(P.5.9.9)
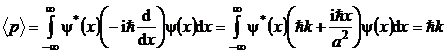 (P.5.9.10)
(P.5.9.10)
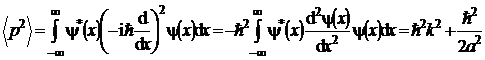 , (P.5.9.11)
, (P.5.9.11)
Inlocuind relatiile (P.5.9.8)-(P.5.9.11) in (P.5.9.2), rezulta:
![]() (P.5.9.12)
(P.5.9.12)
P.5.10. Se considera un electron
(![]() kg) aflat intr-o groapa de potential cu pereti infiniti,
de latime
kg) aflat intr-o groapa de potential cu pereti infiniti,
de latime ![]() (fig. P.5.26.1) definita de potentialul:
(fig. P.5.26.1) definita de potentialul:
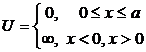 (P.5.10.1)
(P.5.10.1)
Sa se
calculeze: a) functiile proprii si valorile proprii corespunzatoare si b)
energiile primelor trei nivele energetice ale electronului si c) probabilitatea
de a gasi electronul in domeniul ![]()
Rezolvare a) Ecuatia Schrödinger
atemporala in domeniul ![]() se scrie:
se scrie:
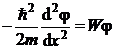 (P.5.10.2)
(P.5.10.2)
iar in domeniul ![]() , deoarece aici particula ar trebui sa aiba energie infinita pentru a
exista.
, deoarece aici particula ar trebui sa aiba energie infinita pentru a
exista.
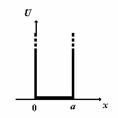
Fig. P.5.10.1. Groapa de potential cu pereti infiniti.
Solutia ecuatiei (P.5.10.2) este de forma:
![]() , (P.5.10.3)
, (P.5.10.3)
unde s-a introdus notatia
![]() (P.5.10.4)
(P.5.10.4)
Din conditiile de
continuitate pentru functiile de unda si derivatele acestora in raport cu ![]() in punctele
in punctele ![]() si
si ![]()
![]() (P.5.10.5)
(P.5.10.5)
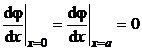 ,
(P.5.10.6)
,
(P.5.10.6)
rezulta:
![]() (P.5.10.7)
(P.5.10.7)
si respectiv valorile proprii ale energiei
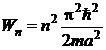 (P.5.10.8)
(P.5.10.8)
Din conditia de normare
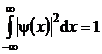 (P.5.10.9)
(P.5.10.9)
rezulta
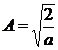 (P.5.10.10)
(P.5.10.10)
si deci functia proprie este de forma
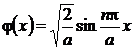 (P.5.10.11)
(P.5.10.11)
b) Din
relatia (P.5.10.8) se obtin valorile primelor trei nivele energetice ale
electronului ![]() (fig. P.5.10.2).
(fig. P.5.10.2).
c) Probabilitatea ![]() de a gasi electronul in domeniul
de a gasi electronul in domeniul ![]() este:
este:
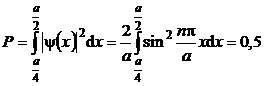 . (P.5.10.12)
. (P.5.10.12)
Fig. P.5.10.2. Diagrama primelor trei nivele energetice ale electronului.
P.5.11. Se considera un atom pentru care
numerele cuantice sunt ![]() , iar
, iar ![]() . Sa se determine: a) starea in care se gaseste atomul si b) momentele
magnetice total si efectiv ale atomului.
. Sa se determine: a) starea in care se gaseste atomul si b) momentele
magnetice total si efectiv ale atomului.
Rezolvare a) sinand seama de numerele cuantice din enuntul
problemei si de notatia consacrata starii rezulta ca aceasta este ![]()
b) Momentul magnetic total
![]() al atomului este (fig. P.5.36.1)
al atomului este (fig. P.5.36.1)
![]() (P.5.11.1)
(P.5.11.1)
iar
![]() (P.5.11.2)
(P.5.11.2)
unde
![]() si
si ![]() . (P.5.11.3)
. (P.5.11.3)
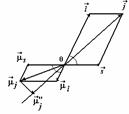
Fig. P.5.11.1. Reprezentarea schematica a momentelor cinetice si
respectiv a momentelor magnetice.
sinand seama ca
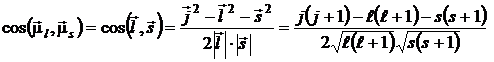 (P.5.11.4)
(P.5.11.4)
si de valorile numerelor cuantice, rezulta
![]() (P.5.11.5)
(P.5.11.5)
Momentul magnetic efectiv al atomului ![]() , definit ca proiectia momentului magnetic total pe directia momentului
cinetic total
, definit ca proiectia momentului magnetic total pe directia momentului
cinetic total ![]() este
este
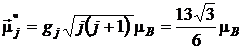 (P.5.11.6)
(P.5.11.6)
![]() (P.5.11.7)
(P.5.11.7)
reprezentand expresia factorului Landé.
P.5.12. Se considera un rotator descris de functia de unda
![]() . (P.5.12.1)
. (P.5.12.1)
Sa se calculeze: a) constanta de normare si b)
valoarea medie a componentei ![]() a momentului cinetic.
a momentului cinetic.
Rezolvare a) Constanta ![]() se calculeaza din conditia de
normare
se calculeaza din conditia de
normare
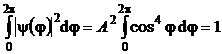 (P.5.12.2)
(P.5.12.2)
rezultand
![]() (P.5.12.3)
(P.5.12.3)
deci
![]() (P.5.12.4)
(P.5.12.4)
b) Valoarea medie a
componentei ![]() a momentului cinetic este data de
relatia
a momentului cinetic este data de
relatia
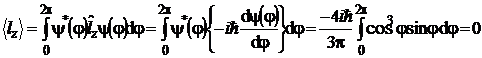 . (P.5.12.5)
. (P.5.12.5)
P.6.1. Sa se gaseasca lungimea de unda pentru care se obtin maxime de interferenta cu o retea cubica simpla pentru o directie data a fasciculului incident de raze X.
Rezolvare In cazul retelei cubice simple maximele de interferenta se obtin din relatiile (ecuatiile Laue):
![]() , (P.6.1.1)
, (P.6.1.1)
![]() , (P.6.1.2)
, (P.6.1.2)
![]() , (P.6.1.3)
, (P.6.1.3)
unde ![]() este constanta retelei,
este constanta retelei,
![]() reprezinta lungimea de
unda,
reprezinta lungimea de
unda, ![]() sunt numere intregi
care determina maximele de interferenta, iar
sunt numere intregi
care determina maximele de interferenta, iar ![]() si
si ![]() sunt unghiurile facute
de raza incidenta respectiv reflectata cu axele
sunt unghiurile facute
de raza incidenta respectiv reflectata cu axele ![]() . Intre unghiurile
. Intre unghiurile ![]() exista relatia:
exista relatia:
![]() (P.6.1.4)
(P.6.1.4)
Rezolvand sistemul de ecuatii (P.6.1.1)-(P.6.1.3) cu conditia (P.6.1.4) se obtine lungimea de unda pentru care se obtin maxime de interferenta sub forma:
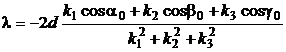 (P.6.1.5)
(P.6.1.5)
P.6.2. Considerand un oscilator
amortizat de masa ![]() si sarcina
si sarcina ![]() sa se calculeze contributia a
sa se calculeze contributia a ![]() astfel de oscilatori pe unitatea de
volum la constanta dielectrica fara a tine seama de interactiunea dintre
oscilatori.
astfel de oscilatori pe unitatea de
volum la constanta dielectrica fara a tine seama de interactiunea dintre
oscilatori.
Rezolvare Pentru oscilatorul descris mai sus ecuatia de miscare este de forma:
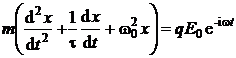 (P.6.2.1)
(P.6.2.1)
unde ![]() este pulsatia la rezonanta,
este pulsatia la rezonanta, ![]() este intensitatea campului electric
cu pulsatia
este intensitatea campului electric
cu pulsatia ![]() , iar
, iar ![]() este timpul de relaxare. Admitandu-se solutii de forma:
este timpul de relaxare. Admitandu-se solutii de forma:
![]() (P.6.2.2)
(P.6.2.2)
din ecuatia (P.6.2.1) se obtine:
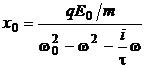 (P.6.2.3)
(P.6.2.3)
Momentul dipolar avand
amplitudinea ![]() mai poate fi scris sub forma
mai poate fi scris sub forma ![]() de unde rezulta pentru polarizabilitatea
de unde rezulta pentru polarizabilitatea
![]() expresia:
expresia:
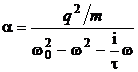 . (P.6.2.4)
. (P.6.2.4)
Polarizarea definita ca momentul dipolar al unitatii
de volum are expresia 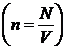 :
:
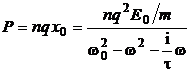 (P.6.2.5)
(P.6.2.5)
Permitivitatea electrica
relativa ![]() a unui mediu izotrop se poate
calcula cu relatia:
a unui mediu izotrop se poate
calcula cu relatia:
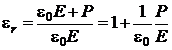 (P.6.2.6)
(P.6.2.6)
astfel ca din ecuatiile (P.6.2.5) si (P.6.2.6) se obtine expresia:
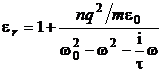 (P.6.2.7)
(P.6.2.7)
P.6.3. Se
considera un conductor de Cu avand sectiunea ![]() aflat la temperatura
camerei. sinand seama ca densitatea de curent electric in Cu se datoreste miscarii
electronilor (un electron pentru fiecare atom) sa se calculeze: a) numarul de
purtatori de sarcina pe unitatea de volum si b) viteza de deplasare a
electronilor pentru un curent egal cu 1 A (model clasic). Se dau pentru Cu: masa atomica
aflat la temperatura
camerei. sinand seama ca densitatea de curent electric in Cu se datoreste miscarii
electronilor (un electron pentru fiecare atom) sa se calculeze: a) numarul de
purtatori de sarcina pe unitatea de volum si b) viteza de deplasare a
electronilor pentru un curent egal cu 1 A (model clasic). Se dau pentru Cu: masa atomica ![]() , densitatea sa
, densitatea sa ![]() , iar numarul Avogadro
, iar numarul Avogadro ![]() si sarcina electrica elementara
si sarcina electrica elementara ![]()
Rezolvare a) Numarul de purtatori din unitatea de volum, ![]() este:
este:
![]() (P.6.3.1)
(P.6.3.1)
b) sinand seama de formula densitatii de curent
![]() (P.6.3.2)
(P.6.3.2)
rezulta:
![]() (P.6.3.3)
(P.6.3.3)
P.6.4. Sa se calculeze conductivitatea
la temperaturi joase ![]() , respectiv inalte
, respectiv inalte ![]() , pentru un material semiconductor avand mobilitatea golurilor
, pentru un material semiconductor avand mobilitatea golurilor ![]() si concentratia impuritatilor
acceptoare
si concentratia impuritatilor
acceptoare ![]() . Se considera atomul acceptor aflat pe un nivel de energie situat in zona
interzisa la o distanta
. Se considera atomul acceptor aflat pe un nivel de energie situat in zona
interzisa la o distanta ![]() deasupra benzii de valenta. Se dau:
constanta Planck
deasupra benzii de valenta. Se dau:
constanta Planck ![]() , constanta Boltzmann
, constanta Boltzmann ![]()
![]() = 9,1 kg si sarcina
electronului
= 9,1 kg si sarcina
electronului ![]()
Rezolvare ¥n cazul temperaturilor joase conductivitatea se calculeaza cu ajutorul relatiei:
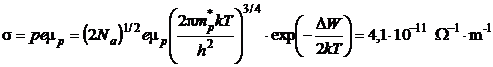 (P.6.4.1)
(P.6.4.1)
La temperaturi ridicate se poate aproxima
![]() (P.6.4.2)
(P.6.4.2)
deci
![]() (P.6.4.3)
(P.6.4.3)
P.6.5. Sa se determine valoarea
energiei medii, ![]() a electronilor din banda de conductie
a unui semiconductor nedegenerat aflat la temperatura
a electronilor din banda de conductie
a unui semiconductor nedegenerat aflat la temperatura ![]()
Rezolvare Energia medie a electronilor din banda de conductie a unui semiconductor nedegenerat este:
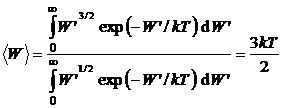 . (P.6.5.1)
. (P.6.5.1)
P.6.6. Fie doua jonctiuni Josephson legate in paralel. Sa se calculeze curentul total care curge prin cele doua jonctiuni si sa se arate ca diferenta de faza de sosire a curentilor pe drumuri diferite da fenomenului un aspect de interferenta.
Rezolvare Pe baza modelului teoretic prezentat in paragraful 19.2.4. curentul total (suma celor doi curenti prin cele doua jonctiuni Josephson) se poate scrie sub forma:
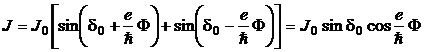 (P.6.6.1)
(P.6.6.1)
unde ![]() este fluxul magnetic. Valoarea maxima
a curentului este:
este fluxul magnetic. Valoarea maxima
a curentului este:
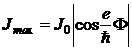 (P.6.6.2)
(P.6.6.2)
maximul expresiei obtinandu-se pentru:
![]() (P.6.6.3)
(P.6.6.3)
Deci curentul va inregistra maxime pentru fluxuri magnetice maxime si respectiv, minime pentru fluxuri magnetice minime.
P.6.7. Se fac doua masuratori de
susceptivitate pentru un material feromagnetic la temperaturile ![]() si
si ![]() mai mari decat temperatura Curie, obtinandu-se
mai mari decat temperatura Curie, obtinandu-se
![]() respectiv
respectiv ![]() . Sa se deduca valorile: a) constantei si b) temperaturii Curie pentru
materialul considerat.
. Sa se deduca valorile: a) constantei si b) temperaturii Curie pentru
materialul considerat.
Rezolvare La temperaturi mai mari decat temperatura Curie materialul este paramagnetic iar susceptibilitatea depinde de temperatura dupa legea:
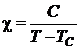 (P.6.7.1)
(P.6.7.1)
unde ![]() si
si ![]() reprezinta constanta si respectiv
temperatura Curie. In conditiile
problemei
reprezinta constanta si respectiv
temperatura Curie. In conditiile
problemei
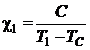
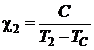 . Rezolvand sistemul celor doua ecuatii rezulta:
. Rezolvand sistemul celor doua ecuatii rezulta:
a) 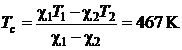 (P.6.7.4)
(P.6.7.4)
si
b) 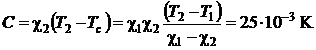 . (P.6.7.5)
. (P.6.7.5)
P.6.8. Se considera o proba de fier
pentru care dependenta dintre inductia magnetica ![]() si intensitatea campului
magnetic
si intensitatea campului
magnetic ![]() este data in fig. P.3.10.1. Aceasta
se afla in interiorul unei bobine avand diametrul
este data in fig. P.3.10.1. Aceasta
se afla in interiorul unei bobine avand diametrul ![]() , sectiunea
, sectiunea ![]() si
si ![]() fiind parcursa de un curent cu
intensitatea
fiind parcursa de un curent cu
intensitatea ![]() . Stiind ca bobina are un intrefier
. Stiind ca bobina are un intrefier ![]() si neglijand dispersia liniilor
de camp in intrefier, sa se calculeze permeabilitatea magnetica
si neglijand dispersia liniilor
de camp in intrefier, sa se calculeze permeabilitatea magnetica ![]() a probei de fier. Se da permeabilitatea absoluta a vidului
a probei de fier. Se da permeabilitatea absoluta a vidului ![]() .
.
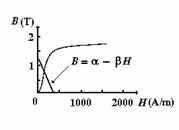
Fig. P.6.8.1. Dependenta dintre inductia magnetica si intensitatea
campului magnetic.
Rezolvare Din legea circuitului magnetic 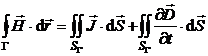 se obtine in conditiile
problemei
se obtine in conditiile
problemei ![]() . Ecuatia dreptei intersecteaza axele in punctele
. Ecuatia dreptei intersecteaza axele in punctele ![]() si
si ![]() . Din intersectia dreptei
. Din intersectia dreptei ![]() (relatiasi a curbei
(relatiasi a curbei ![]() (fig. P.3.10.1.) rezulta
(fig. P.3.10.1.) rezulta ![]()
P.7.1. Sa se calculeze temperatura unui
gaz format din atomi de cesiu, daca se cunoaste ca raportul intensitatii
componentelor liniei de rezonanta (care este un dublet cu lungimile de unda ![]() , respectiv
, respectiv ![]() ) are valorea
) are valorea ![]() . Se dau: viteza luminii
. Se dau: viteza luminii ![]() m/s, constanta Planck
m/s, constanta Planck ![]() si constanta Boltzmann
si constanta Boltzmann ![]()
Rezolvare In conditii de echilibru termodinamic corespunzator
temperaturii ![]() pe baza statisticii Boltzmann
raportul populatiilor a doua nivele este dat de relatia:
pe baza statisticii Boltzmann
raportul populatiilor a doua nivele este dat de relatia:
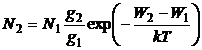 (P.7.1.1)
(P.7.1.1)
unde![]()
![]() reprezinta numarul de atomi aflati
in stararile de energie
reprezinta numarul de atomi aflati
in stararile de energie ![]() si respectiv
si respectiv ![]() , iar
, iar ![]() este raportul ponderilor statistice (degenerescentele)
corespunzatoare. Considerand ca intensitatile liniilor cu lungimile de unda
este raportul ponderilor statistice (degenerescentele)
corespunzatoare. Considerand ca intensitatile liniilor cu lungimile de unda ![]() , si respectiv
, si respectiv ![]() sunt proportionale cu numarul
corespunzator de atomi excitati,
sunt proportionale cu numarul
corespunzator de atomi excitati, ![]() si
si ![]() si aproximand
si aproximand ![]() se obtine pentru temperatura
valoarea:
se obtine pentru temperatura
valoarea:
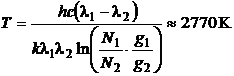 (P.7.1.2)
(P.7.1.2)
P.7.2. Cu ajutorul unui fascicul laser
se iradiaza sub incidenta normala doua lame de grosimi ![]() si
si ![]() . Introducand pe rand cele doua lame in fascicule se constata ca ele
transmit
. Introducand pe rand cele doua lame in fascicule se constata ca ele
transmit ![]() si respectiv
si respectiv ![]() din fluxul luminos. Sa se calculeze
coeficientul de absorbtie
din fluxul luminos. Sa se calculeze
coeficientul de absorbtie ![]() al materialului din care sunt confectionate
lamele.
al materialului din care sunt confectionate
lamele.
Rezolvare sinand seama de legea lui Lambert-Beer
![]() (P.7.2.1)
(P.7.2.1)
se obtine pentru coeficientul de absorbtie valoarea:
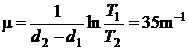 (P.7.2.2)
(P.7.2.2)
P.7.3. Se considera un sistem laser care functioneaza cu doua nivele energetice in starea de regim stationar. Sa se deduca conditia care trebuie indeplinita astfel incat emisia spontana sa corespunda emisiei induse.
Rezolvare Echilibrul termodinamic al radiatiei este atins cand numarul proceselor de absorbtie este egal cu numarul proceselor de emisie:
![]() . (P.7.3.1)
. (P.7.3.1)
¥mpartind relatia
(P.7.3.1) cu ![]() si considerand
si considerand ![]() , rezulta :
, rezulta :
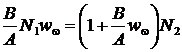 (P.7.3.2)
(P.7.3.2)
sinand seama ca numarul de moduri pe unitatea de volum ale unui oscilator in vid este :
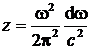 , (P.7.3.3)
, (P.7.3.3)
si densitatea de radiatie in intervalul de frecventa ![]() este :
este :
![]() (P.7.3.4)
(P.7.3.4)
unde ![]() reprezinta numarul de
fotoni pe unitatea de volum, numarul de fotoni pe mod se poate scrie sub forma:
reprezinta numarul de
fotoni pe unitatea de volum, numarul de fotoni pe mod se poate scrie sub forma:
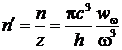 , (P.7.3.5)
, (P.7.3.5)
iar relatia dintre coeficientii Einstein devine:
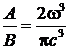 . (P.7.3.6)
. (P.7.3.6)
Introducand relatia (P.7.3.6) in (P.7.3.2) conditia ceruta poate fi scrisa sub forma:
![]() (P.7.3.7)
(P.7.3.7)
¥n relatia (P.7.3.7) termenul ![]() corespunde absorbtiei induse,
corespunde absorbtiei induse, ![]() emisiei spontane, iar
emisiei spontane, iar ![]() emisiei induse, adica emisia spontana
corespunde emisiei induse daca ar fi un singur foton pe mod.
emisiei induse, adica emisia spontana
corespunde emisiei induse daca ar fi un singur foton pe mod.