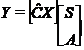Network coding

Securitate

Network coding afecteaza securitatea datelor atat in moduri favorabile, cat si nefavorabile, in functie de aplicatie. Exemplul urmator ilustreaza situatia.

Exemplul 1

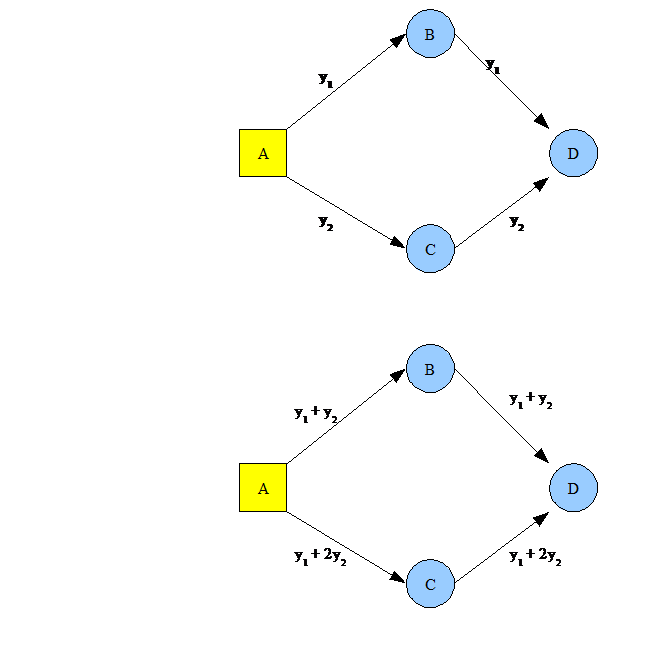
Consideram reteaua simpla din figura, formata din doua canale de capacitate unitara. Doua surse independente de informatie, cu rata de transmisie 1 sunt localizate in nodul A, iar un utilizator din nodul D a platit pentru a primi informatia din ambele surse (spre exemplu, doua filme). Scopul poate fi atins prin stor e-and-forward, ca in figura a, sau prin codare, ca in figura b. Consideram acum un inamic, ce are acces la o singura muchie a retelei. Daca transmisia este organizata ca in figura a, el primeste informatia complta de la o sursa. Daca transmisia este organizata ca in figura b, adversarul primeste un bit de informatie legat de perechea , dar informatia poate fi inutila.

Consideram acum un inamic capabil nu doar sa observe, ci si sa modifice datele de pe o muchie. In acest caz, transmisia conform schemei din figura a este mai buna, deoarece utilizatorul poate primi totusi informatia dintr-o sursa.

Vom considera doua cazuri generale in care un adversar are acces la un anumit numar de muchii ale retelei.

In primul caz, adversarul doar asculta. Scopul lui poate fi sa reduca nesiguranta legata de informatia transmisa utilizatorului. Intr-un alt scenariu, scopul lui poate fi chiar sa decodeze o fractiune din informatia pe care o observa. Vom vedea cum network coding liniar il poate ajuta sau incurca pe adversar, in functie de scopul sau. Vom vedea de asemenea cum putem construi coduri care sa previna interceptarea informatiei.

In al doilea caz, adversarul poate sa si modifice o parte din pachetele interceptate. Modificarea unui anumit nuar de pachete din retele ce pot doar ruta informatia au ca rezultat doar o receptie incorecta, dar in cazul codarii liniare pentru acelati numar de pachete efectele pot sa fie mai periculoase.

Interceptarea informatiei

Consideram cazul retelelor multicast, in care un adversar poate avea acces la legaturi la alegere, si are o acces la o putere computationala nelimitata. Scopul nostru este sa maximizam rata de transmisie multicast fara a oferi informatii adversarului. Pentru acest lucru, sursa trebuie sa introduca o anumita redundanta in datele trimise, folosind o schema de codare. Intrebarea care apare este cum va interactiona aceasta schema de codare cu network code-ul folosit de nodurile retelei.

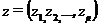Problema poate fi formulata matematic astfel. Presupunem ca min-cut-ul pentru fiecare receptor este n. Notam cu variabilele aleatoare asociate cu cele k simboluri de informaaie pe care sursa doreste sa le trimita in siguranta, variabilele aleatoare asociate cu simbolurile codate pe care sursa le transmite catre receptori si variabilele aleatoare asociate cu simbolurile interceptate de adversar.

Vom face diferenta intre doua nivele de securitate. O schema de codare este teoretic sigura din punct de vedere informational daca s este complet determinat (decodabil) de y, iar incertitudinea asupra lui s nu este redusa de cunoasterea lui z, deci

Pe de alta parte, o schema de codare este slab securizata daca incertitudinea asupra unui simbol particular nu este redusa de cunoasterea lui z, deci

,

dar este posibil ca H(s/z) < H(s). Exemplul urmator ilustreaza diferenta intre cele doua situatii

Exemplu. Pentru reseaua din figura anterioara, o schema sigura de codare a informatiei nu n = 2, k = 1, si poate fi organizata in felul urmator. Daca bitul transmis , atunci 00 sau 11 va fi transmis pe canal cu o probabilitate egala. In mod similar, daca bitul sursei este egal cu 1, atunci 01 sau 10 vor fi transmisi pe canal cu probabilitate egala. Deci, cuvantul de cod este ales aleator din multimea daca bitul sursa este 0 si din ddaca bitul sursa este 1.

Este usor de observat ca, daca se cunoaste bitul sau bitul nu este redusa incertitudinea legata de , iar cunoasterea atat a lui , cat si a lui este suficienta pentru determinarea lui .

Exemplu. Figura b prezinta cazul unei securitati slabe, folosind si . Daca, spre exemplu,siiau valori aleatoare, distribuite uniform in , atunci . Daca presupunem ca adversarul intercepteaza valoarea si incearca sa ghiceasca , este usor de vazut ca poate lua orice valoare din cu o probabilitate egala (). Cu alte cuvinte, probabilitatea ca adversarul sa faca o eroare este aceeasi cu cea din cazul in care ar incerca sa ghiceasca valoarea lui .

Teoria securitatii informatiei

Consideram un scenariu punct-la-punct, in care sursa poate transmite n simboluri de date catre receptor si un adversar poate accesa oricaredintre aceste simboluri. Este cunoscut faptul ca numarul maxim de simboluri pe care sursa le poate comunica in siguranta receptorului din punct de vedere teoretic este k = n - .

Acest lucru poate fi obtinut folosind cu unn cod liniar MDS , de dimensiuni . Cuvintele de cod dintr-un cod liniar sunt vectori intr-un subspatiu -dimensional al unui spatiu -dimensional. Matricea generatoare G asociata are dimensiunea x , iar matricea de paritate h are dimensiunea -x . Liniile lui G formeaza o baza a subspatiului C, iar liniile lui H formeaza o baza a spatiului ortogonal. Deci, pentru orice cuvant de cod .

Pentru a crea un network code sigur din punct de vedere informational, ce poate transmite k simboluri, vom folosi un cod MDS cu = n si = n - k, ce are k valori ale sindromului. Cele k simboluri de informatie sunt luate ca sindromuri ce specifica ??. Cuvantul transmis este ales uniform dintre vectorii submultimii rezultate. Decodorul ce primeste un vector y poate recupera simbolurile de informatie prin calculul sindromului Hy al cuvantului receptionat.

Sa presupunem ca adversarul intercepteaza = n - k = simboluri ale lui y. Intrebarea este daca poate deduce din aceste simboluri informatii despre sindrom. Raspunsul este nu, deoarece fiecare din cei vectori ce contin cele simboluri interceptate apartine unei alte submultimi. De altfel, oricare din cei vectori, sa spunem si difera in cel mult -simboluri. Dar distanta minima este , ti astfel niciunul dintre acesti doi vectori nu poate apartine aceleiasi submultimi.

Codul folosit in exemplul 2 este un cod cu repetitie [2, 1] peste , cu matricea de paritate

H = [1 1],

submultimile si si distanta 2.

Acum, sa consideram un network code specific, folosit pentru a transmite prin multicast n simboluri de la o sursa de informatie la N receptoare, peste o resea aciclica G = (V, E) si sa presupunem ca adversarul intercepteaza muchii ale lui G. Intrebarea care apare este daca, folosind acelasi network code, sursa poate transmite prin multicast simboluri in siguranta, in conditiile in care mai intai este aplicat codul de securitate descris mai sus, transformand cele k simboluri in n simboluri. Raspunsul este ca in general nu este posibil, dupa cum este ilustrat in urmatorul exemplu.

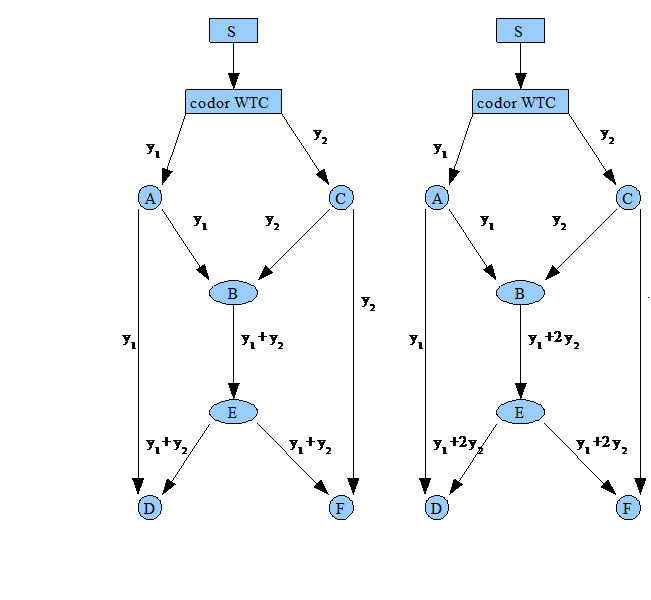
Exemplu. Consideram reteaua fluture din figura, unde avem n = 2, k = 1 si = 1. Daca sursa aplica schema de codare din exemplul anterior, pe baza unui cod MDS peste cu H = [1 1], si reteaua din figura a, adversarul va putea afla imediat bitul transmis de sursa daca asculta oricare din muchiile BE, EF, ED. Acest lucru se intampla din cauza ca vectorul de codare (1 1) arata produsul dintre o linie a lui H si cuvantul transmis y, deci arata unul din bitii sindromului. Deci, network code-ul elimina securitatea oferita de codarea canalului.

Totusi, daca codul de retea este schimbat astfel incat nodul B isi combina intrarile peste campul si vectorul de codare BE este unde este un element primitiv din , codul de canal r[mne sigur, deci adversarul nu poate afla informatia accesand o singura muchie a retelei. In general, codul canalului ramane sigur cu orice network code in care vectorul de codare al muchiei BE este liniar independent fata de (1 1).

In general, sursa poate transmite prin multicast simboluri in siguranta daca mai intai aplica un cod de securitate bazat pe un cod MDS cu o matrice de paritate H de dimensiune k x n, iar daca network code-ul este construit in asa fel incat nicio combinatie liniara de = n - k sau mai putini vectori de codare nu apartine spatiului parcurs de liniile lui H. Asta inseamna ca oricare vectori de codare impreuna cu liniile lui H trebuie sa nu formeze o baza a spatiului n-dimensional. Acest lucru garanteaza ca simbolurile transmise pe muchiile retelei nu pot fi folosite pentru a deduce informatie despre bitii sindromului.

Pentru a demonstra aceste argumente, putem folosi si teoria informatiei. Consideram o multime avand |W| = ( numarul de muchii interceptate de atacator), iar este matricea cu liniile egale cu vectorii de codare asociati muchiilor interceptate in W. Consideram H(s, y, z) cu cerinta de secruitate H(s/z) = H(s) pentru a obtine

Deoarece exista posibilitatea de a alege muchiile astfel incat , rata maxima de transmisie in siguranta este limitata de

Daca limita este atinsa, avem H(s/y, z) = 0 si in consecinta sistemul de ecuatii

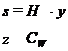
are solutie unica pentru toate matricile W pentru care .

In concluzie, am aratat ca, daca avem un cod de scuritate dat, putem gasi un cod de retea care nu afecteaza securitatea. Procedeul invers este de asemenea posibilS putem incepe cu un cod de retea fix, si apoi sa selectam un cod de securitate potrivit, care sa nu fie compromis de network code.

Securitate slaba

Sa consideram din nou o retea multicast an care min-cut-ul catre oricare receptor este egal cu n. Daca securitatea slaba, asa cum a fost definita mai sus, este suficienta, putem trimite informatie catre receptori cu o rata egala cu n, chiar daca adversarul poate asculta = n - 1 muchii.

Ideea de baza este simpla. Cream y prin codarea simbolurilor sursei s cu o matrice inversabila A, spre exemplu, y = As. Adversarul va putea intercepta z = By = Bas, unde matricea B de dimensiune x n are liniile egale cu vectorii de codare de pe muchiile interceptate. Este suficient sa selectam matricea A si network code-ul astfel incat, pentru orice matrice B, sa nu existe un vector astfel incat . Acest lucru este intotdeauna posibil, daca folosim un cod peste un camp finit suficient de mare.

Pentru a vedea cum aceasta constructie garanteaza securitatea slaba mentionam ca, daca incepem cu o distributie uniforma a elementelor campului finit, iar apoi efectuam orice transformare liniara, distribvutia rezultata va fi de asemenea uniforma. Spre exemplu, daca si sunt distribuite uniform peste , atunci si este distribuit uniform. Astfel, daca o combinatie liniara interceptata nu permite adversarului sa decodeze simbolul sursei , distributia de probabiliate a lui conditionata de valorile interceptate este de asemenea uniforma.

Modificarea bizantina

Eroarea bizantina se refera la orice eroare dintr-un sistem distribuit aparuta din cauza unei greseli dintr-unul din subsistemele componente. Deoarece una dintre cerintele network coding este ca mai multe noduri ale retelei sa se comporte conform modelului (spre exemplu, sa efectueze combinatii liniare asupra intrarilor pentru a produce iesiri), acesa este un proces distribuit, vulnerabil atacurilor de tip bizantin.

Un atac de tip bizantin poate, spre exemplu, furniza un numar de pachete modificate receptorului, iar acesta sa decodeze toate pachetele sursei incorect. Putem distinge tipuri diferite de atac, in functie de puterea atacatorului, modul de comunicatie dintre sursa si receptor, nivelul de protectie dorit. Spre exemplu, atacatorul poate sa asculte toate muchiile retelei, dar sa modifice doar dintre ele, sau poate asculta doar cele muchii pe care le poate modifica. Poate exista de asemenea un canal secret, ce nu poate fi accesat de atacator, pe care sursa sa poata transmite cativa biti receptorului.

Pe partea receptorului, putem fi interesati doar in detectia unui atac bizantin pentru a ignora pachetele corupte, sau putem sa dorim filtrarea informatiei transmise de sursa in timp ce atacul avea loc. In toate cazuril, calea naturala de protectie a datelor este prin introducerea unui cod corector de erori astfel incat pachetele sa transporte nu doar datele, dar si informatie redundanta.

Vom considera un atac bizantin in care exista un canal secret de rata mica intre sursa si fiecare dintre receptori, intr-o retea multicast in care min-cut-ul dintre sursa si fiecare receptor este n. Fiecare destinatar este interesat in recuperarea anumitor informatii transmise de sursp, iar atacatorul poate observa toate transmisiile si poate insera pachete corupte. In acest caz, exista algoritmi de timp polinomiali pentru codare/decodare ce permit receptorilor sa recupereze in siguranta informatia de la sursa la o rata de n - . Aceasta este rata maxima ce poate fi atinsa, daca rata canalului secret este zero comparativ cu rata suportata de retea.

Vom considera o schema practica, in care sursa produce n pachete de lungime egala cu L simboluri de informatie, iar nodurile retelei pot combina aleator si schimba combinatii liniare ale pachetelor sursa. Un header de lungime n adaugat fiecarui pachet specifica combinatiile liniare pe care pachetul le transporta. Fie S matricea de dimensiune n x (L + n), ale carei linii sunt pachetele transmise de sursa, si care contine n x n matrici unitate I. Receptorul va primi

,

unde Z este matricea de dimensiune x (L + n) ale carei linii sunt pachetele corupte de atacator, iar Y este setul de pachete receptionat. Matricea C este matricea de transfer, de dimensiune n x n de la sursa la receptori, iar matricea este matricea de transfer de dimensiuni n x de la adversar la receptor.

Deoarece operatiile din nodurile de codare sunt efectuate la nivel de simbol, matricea identitate I continuta in S trece prin aceleasi transformari ca si matricea originala S. Deci Y contine matricea

,

pentru o matrice oarecare L continuta in Z. Va rezulta

Matricea E contine efectele atacului. Receptorul stie matricile Y si si trebuie sa decodeze S.

Pentru a ajuta receptorul, sursa poate opera in modul urmator. Mai intai, selecteaza aleator n + L valori din campul si creeaza matricea de maritate de dimensiune (n + L) x c, unde c este un parametru de design

Sursa comunica matricea H catre toti receptorii folosind canalul secret. Aceasta comunicatie are loc o singura data.

In plus, de fiecare data cand sursa produce n pachete de lungime L simboluri, grupate an matricea S de dimensiune n x (n + L), trimite pe canalul sigur matricea P = SH. Dimensiunea informatiei transmise pe canalul secret pentru matrice P (n x c) poate fi arbitrar de mica in comparatie cu lungimea pachetelor L.

Receptorul poate profita de aceasta informatie suplimentara. Mai intai, calculeaza proiectia matricei Y peste H

pentru a afla matricea X = EH. Coloanele matricei vor defini acelasi spatiu vectorial ca si coloanele lui E, deci E = XA pentru orice matrice A. Atunci, receptorul poate afla matricea Y ca fiind