Definitia derivatei intr-un punct
f:E R, xoIE, xo - punct de acumulare a lui E:
f'(x0) = 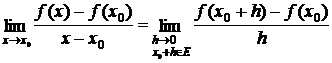
fs'(x0) = 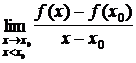 , fd'(x0)
=
, fd'(x0)
= 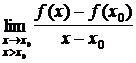
f'(x0) = fs'(x0) = fd'(x0)
Interpretarea geometrica:
daca f'(x0)IR, y - f(x0) = f'(x0)(x - x0) este ecuatia tangentei la graficul functiei f in punctul A(x0,f(x0));
daca f este continua in x0, fd'(x0) = + , fs'(x0) = - , sau invers, x0 este punct de intoarcere al graficului;
daca f este continua in x0 si exista derivatele laterale in x0, cel putin una fiind finita, dar f nu este derivabila in x0, x0 este punct unghiular al graficului.
Reguli de derivare
f,g:E R, f,g derivabile in xIE:
1. (f + g)'(x) = f'(x) + g'(x);
2. (cf)'(x) = cf'(x), cIR;
3. (f g)'(x) = f'(x) g(x) + f(x) g'(x)
4.
daca
g(x) 0, 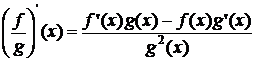 ;
;
5. daca f:I J, g:J R, f derivabila in x0II si g derivabila in y0 = f(x0), atunci (gof)'(x0) = g'(y0)f'(x0);
Derivatele functiilor elementare
|
Functia (conditii) |
Derivata (conditii) |
|
C |
0 |
|
xn, nIN* |
nxn-1 |
|
xr, rIR, x>0 |
rxn-1 |
|
|
|
|
logax, a 1, a>0, x>0 |
|
|
ln x, x>0 |
|
|
ax, a 1, a>0, x>0 |
ax ln a |
|
ex |
ex |
|
sin x |
cos x |
|
cos x |
-sin x |
|
tg x, x |
|
|
ctg x, x |
|
|
arcsin x, xI[0,1] |
|
|
arcos x, xI[0,1] |
|
|
arctg x |
|
|
arcctg x |
|
Derivata functiilor compuse
|
Functia (conditii) |
Derivata (conditii) |
|
un, nIN* |
nun-1 u' |
|
ur, rIR, u>0 |
uxn-1 u' |
|
|
|
|
logau, a 1, a>0, u>0 |
|
|
ln u, u>0 |
|
|
au, a 1, a>0 |
au ln a u' |
|
eu |
eu u' |
|
sin u |
cos u u' |
|
cos u |
- sin u u' |
|
tg u, cos u 0 |
|
|
ctg u, sin u 0 |
|
|
arcsin u, uI[-1,1] |
|
|
arccos u, uI[-1,1] |
|
|
arctg u |
|
|
arcctg u |
|
|
uv , u>0 |
uv v' ln u + v uv-1 u' |