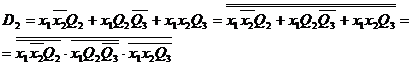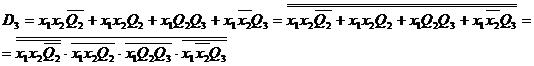Circuitele logice secventiale sunt circuite de comutare la care starea externa(iesirea), la un moment dat, depinde nu numai de starea intrarilor la momentul de timp considerat, ci si de starile anterioare ale acestuia. Din acest motiv circuitele logice secventiale(CLS) trebuie sa aiba memorie in care sa se pastreze informatia referitoare la evolutia lor anterioara.
Definirea circuitelor logice secventiale se bazeaza pe introducerea conceptului de stare interna. Informatia pastrata in memorie si pe baza careia se cunoaste complet evolutia anterioara a circuitului se numeste stare interna a acestuia. Existenta starilor interne la aceste circuite, face ca evolutia lor in timp sa fie complet definita prin starile interne succesive in care circuitul se poate afla. Deasemenea, spre deosebire de circuitele logice combinationale, existenta starilor interne face ca timpul sa apara ca variabila explicita in functionarea acestor circuite.
Uu circuit logic secvential este un circuit de prelucrare a informatiilor discrete, in care se pun in evidenta urmatoarele seturi de marimi :
un set al variabilelor de intrare: X=;
un set al variabilelor de iesire: Z=;
un set al variabilelor de stare: Y=.
Dupa modul de functionare si constructie circuitele logice secventiale se impart in doua categorii: circuite logice secventiale asincrone(CLSA) si circuitele logice secventiale sincrone(CLSS) la care comutarile de stare au loc doar la momente de timp bine determinate marcate prin impulsuri obtinute de la un generator de sincronizare.
Schema
bloc generala a unui circuit logic secvential este urmatoarea 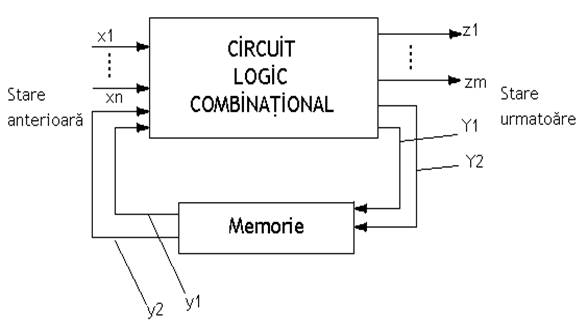
 a)
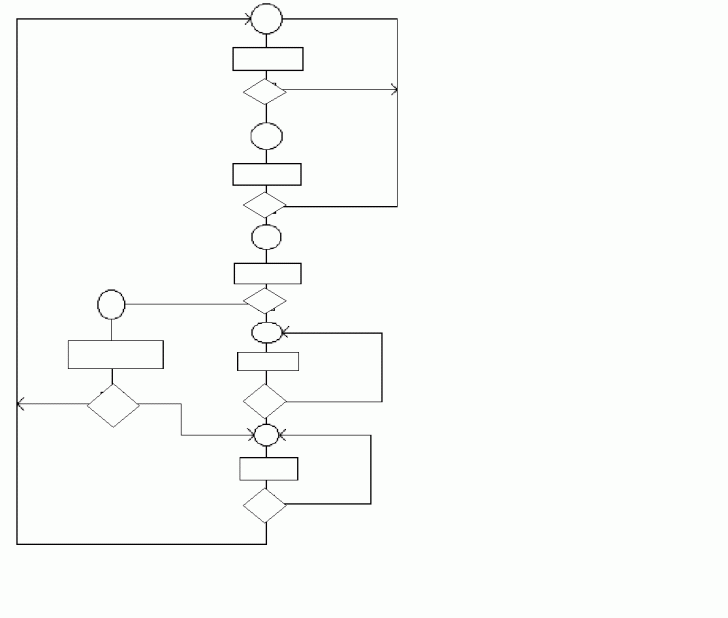
Intocmirea grafului de tranzitii si a organigramei
a)
Intocmirea grafului de tranzitii si a organigramei
S1
Citeste "s"
NU
s
DA
S2
Citeste "a"
a NU
S3
Citeste "l"
NU l
S6
DA
S4
Citeste "p" Citeste "p"
DA NU NU
p p
DA
S5
Citeste "l"
NU
l
DA
Am definit urmatoarele stari posibile:
S1 = citeste pe "S" (s)
S2 = citeste pe "a" (a)
S3 = citeste cratima dupa "sa"
S4 = citeste spatiul alb sau alte semene de punctuatie
S5 = citeste litere si alte caractere
S6 = citeste spatiul alb sau alte semen de punctuatie dupa "sa"
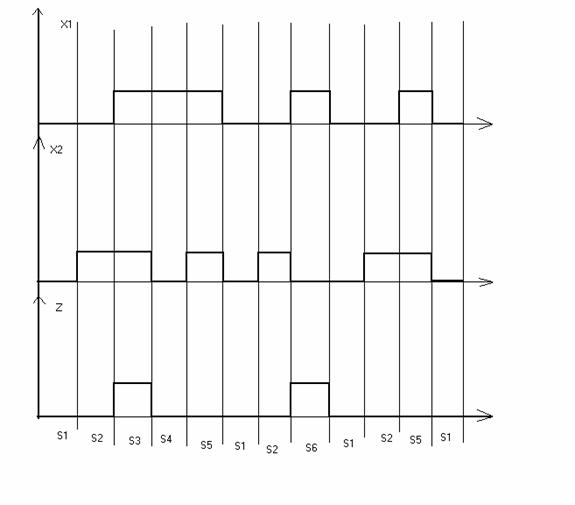
f(S1, 00) = S1 f(S1, 01) = S2 f(S1, 11) = * f(S1, 10) = *
f(S2, 00) = S2 f(S2, 01) = S2 f(S2, 11) = S3 f(S2, 10) =S6
f(S3, 00) = * f(S3, 01) = S2 f(S3, 11) = S3 f(S3, 10) = S4
f(S4, 00) = * f(S4, 01) = * f(S4, 11) = S3 f(S4, 10) = S4
f(S5, 00) = S1 f(S5, 01) = S2 f(S5, 11) = S5 f(S5, 10) = S4
f(S6, 00) = S1 f(S6, 01) = S2 f(S6, 11) = * f(S6, 10) = S6
Tabela primitiva a starilor
|
x Sk |
|
|
|
|
Z |
|
S1 |
S1 |
S2 |
|
|
|
|
S2 |
S1 |
S2 |
S3 |
S6 |
|
|
S3 |
|
S2 |
S3 |
S4 |
|
|
S4 |
|
|
S3 |
S4 |
|
|
S5 |
S1 |
S2 |
S5 |
S4 |
|
|
S6 |
S1 |
S2 |
|
S6 |
|
Graful de tranzitii:
Oricarui circuit logic secvential i se poate atasa un graf orientat si marcat. Graful de tranzitii constituie reprezentarea grafica a modelului matematic a unui CLS:
Algoritmul dupa care se intocmeste graful unui CLS:
a) mutimii starilor circuitului ii corespunde multimea varfurilor sau nodurilor grafului.
b) Daca Si si Sj apartin lui S sunt stari de CLS legate prin relatia Sj=f(xi,Si) atunci nodul sau varful Si se leaga de Sj printr-un arc orinetat de la Si la Sj, arcul astfel obtinut este marcat prin semnalul de intrare care a determinat tranzitia respectiva
c) Pe graf se vor reprezenta iesirile circuitului, dar modul de reprezentare depinde de tipul circuitului, si anume la circuite de tip Mealy pe (Si,Sj) langa intrare se va trece si iesirea corespunzatoare, in timp ce la cele de tip Moore iesirea se va trece in nodurile retelei
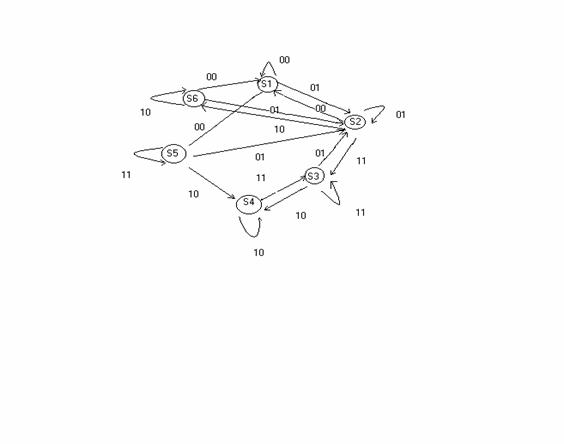
b) Codificarea starilor rezultate in urma elborarii grafului respectiv organigramei
Reducerea numarului de stari
Reducerea numarului de stari consta in alipirea unui numar de stari din matricea primitiva a starilor (dupa anumite reguli) si obtinerea matricei reduse a starilor. Cele doua automate, cel initial si cel redus, sunt echivalente.
Alipirea sau fuzionarea a doua linii a matricei primitive a starilor (caracterizate de starile stabile i si j) devine posibila daca se respecta urmatoarea regula: doua linii ale matricei primitive a starilor caracterizate de starile stabile i si j se pot alipi , obtinandu-se in felul acesta o forma redusa, daca tranzitiile din aceste stari stabile conduc, prin alipirea acelorasi valori ale variabilelor de intrare, in starea stabila viitoare unica k. Alipirea liniilor (starilor) trebuie sa tina cont si de un criteriu suplimentar si anume, acela al concordantei iesirilor. In felul acesta, procesul de minimizare al automatului secvential se extinde si asupra sectiunii logice de generare a iesirilor. Din cele doua reguli rezulta urmatorul criteriu practic : cele doua linii pot fuziona, in cazul in care in locatiile corespunzatoare celor doua linii se afla una din urmatoarele situatii :

Pentru a se putea pune in evidenta toate alipirile posibile intre starile automatului se construieste poligonul alipirilor. In nodurile acestuia se trec starile nereduse, iar pe segmente de dreapta se vor marca alipirile posibile. Dupa intocmirea poligonului trebuie aleasa solutia de fuzionare optima . In acest sens, daca in cazul general k - stari nereduse formeaza, in poligonul alipirilor, un contur poligonal complet (interior sau exterior), rezulta ca cele k stari nereduse se pot alipi obtinandu-se o singura stare echivalenta. In cazul in care prin alipire s-a obtinut din numarul total de stari nereduse o singura stare redusa, circuitul logic secvential degenereaza intr-unul combinational.
Doua stari Si si Sj sunt echivalente daca pentru orice secventa de intrari de lungime arbitrara aplicata automatului aflat in starea Si sau Sj se obtine aceeasi secventa de iesire. Altfel spus starile Si si Sj sunt echivalente daca nu pot fi distinse prin observarea iesirilor automatului.
S-a redus stare S1 si S2 si starea echivalenta s-a notat cu A:
S1 S1 S2 * *
S2 S1 S2 S3 S6
A S1 S2 S3 S6
Starea S3 -> B, S4 -> C, S5 -> D, S6 ->E
S-au
obtinut 5 noi straturi si in vederea codificarii starilor trebuie sa introducem
o noua variabila de stare deoarece regula de codificare este: 2![]()
Intocmimirea poligonul tranzitiilor:
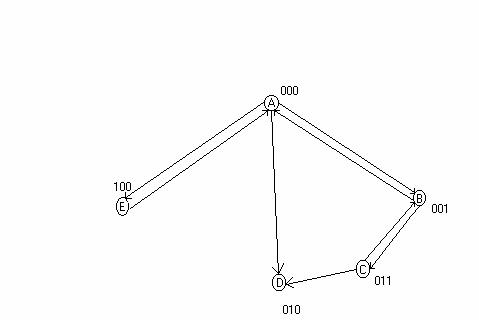
|
x Sk |
|
|
|
|
Z |
|
A |
S1 |
S2 |
S3 |
S6 |
|
|
B |
|
S2 |
S3 |
S4 |
|
|
C |
|
|
S3 |
S4 |
|
|
D |
S1 |
S2 |
S5 |
S4 |
|
|
E |
S1 |
S2 |
|
S6 |
|
|
x y1y2y3 |
|
|
|
|
Z |
|
000(A) |
S1 |
S2 |
S3 |
S6 |
|
|
001(B) |
|
S2 |
S3 |
S4 |
|
|
010(C) |
|
|
S3 |
S4 |
|
|
011(D) |
S1 |
S2 |
S5 |
S4 |
|
|
100(E) |
S1 |
S2 |
|
S6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
d) Intocmirea diagramei starilor urmatoare (la momentul de timp "t+1")
|
x y1y2y3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e) Determinarea variabilelor de excitatie pentu automatele elementare ce compun registrul de stari.
In figura este prezentat automatul elementar de tip D. In prezenta impulsului de tact T, functionarea automatului D este descrisa de ecuatia: Qt+1=Dt
Acest bistabil are o intrare sincroana notata cu D care determina starea bistabilului. Tabeleul de funcitonare si tabelul excitatiior sunt date in urmatoarele 2 tabele:
|
Dt |
Qt+1 |
|
0 |
|
|
|
|
|
Qt |
Qt+1 |
Dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Bascularea automatelor elementare are loc o singura data in prezenta unui impuls de tact. In raport cu momentul aparitiei impulsului automatele D comuta pe frontul anterior al impulsului de tact.
Configuratia circuitului secvential sincron realizat cu automate elementare de tip D.
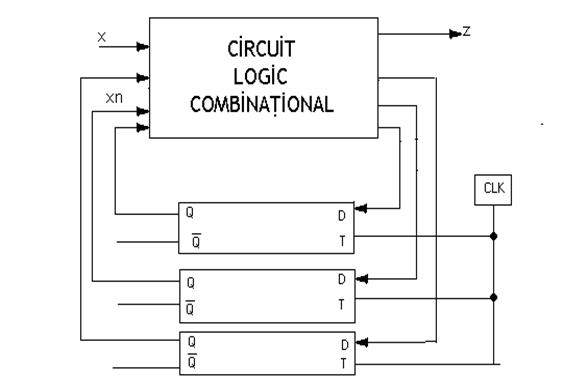
Determinarea Expresiei lui D1:
|
Q1 Q2 Q3 x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1 Q2 x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Nu avem implicanti primi:
_ _ _ _
D![]() = x1x2
= x1x2![]()
Determinarea expresiei lui D2:
|
Q1 Q2 Q3 x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1 Q2 x1x2 |
|
|
|
|
|
|
|
|
|
|
|
01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D![]() =
=![]()
Determinarea expresiei lui D3:
|
Q1 Q2 Q3 x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q1 Q2 x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D3=![]()
f) Obitinerea expresiilor logice ale variabilelor de iesire alea automatului
|
Q1 Q2 Q3 x1x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z= Q1![]() Q3
Q3
g) Implementarea cu circuite integrate (automate elementare de tip D si porti logice)
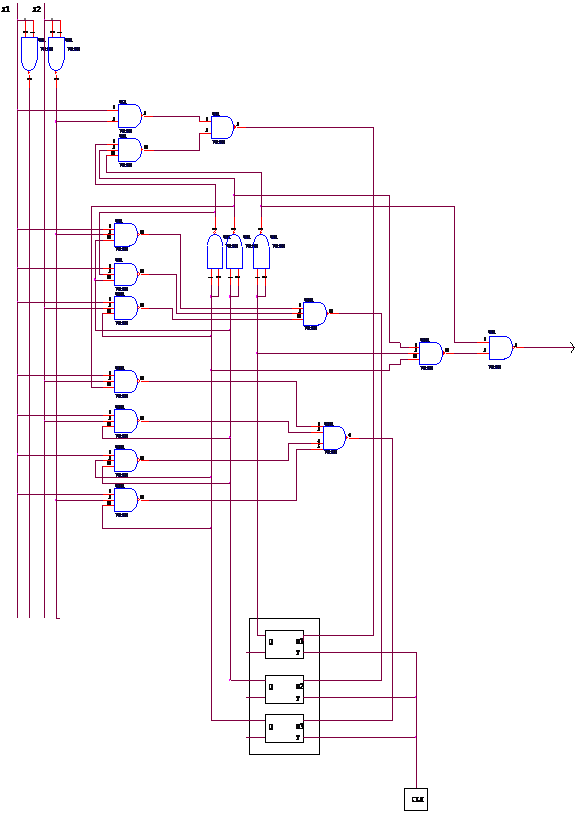
Dupa obtinerea schemei trebuie testata functionarea acesteia atat analizand diverse secvente intrare-iesire cat si pentru un ciclu de functionare complet. Aceasta analiza urmareste punerea in evidenta a unor situatii de avarie. Tot in cursul analizei se urmareste daca este posibila simplificarea schemei obtinute, prin inlaturarea unor structuri redundante si de asemenea completarea schemei cu o serie de elemente auxiliare : de amplificare, de eliminare a hazardului, de adaptare a nivelelor semnalelor pentru comanda unor elemente de executie.
Analiza schemei obtinute presupune simularea schemelor pe calculator. Aceasta implementare se realizeaza cu porti logice "SI-NU", si se face in felul urmator : functiile de excitatie ale automatului si functiile iesirilor se neaga de doua ori pentru a putea fi implementate cu porti logice "SI-NU"
_ _ _ _
D1=x1x2![]() , ramne la fel, nu se modifica.
, ramne la fel, nu se modifica.