Cuprins...........................2
Introducere...........................3
Capitolul 1. Procese de invatare in sisteme cu inteligenta artificiala.....5
Capitolul 2. Elemente de neurodinamica..............9
2.1. Modelul general al unei retele neuronale...........9
2.2. Retele neuronale multistrat...............11
Capitolul 3. Modelul perceptronului..................13
3.1. Perceptronul cu un singur strat............13
3.2. Algoritmul de instruire................15
3.3. Limitele perceptronului.................16
Capitolul 4. Propagarea inapoi a erorii...............17
4.1. Functia criteriu...................17
4.2. Algoritmul de propagare inapoi..............19
Capitolul 5. Arhitecturi moderne de retele neuronale........21
5.1. Retele neuronale probabilistice.............21
5.2. Retele neuronale fuzzy.................22
Capitolul 6. Aplicatii ale retelelor neuronale............24
6.1. Retele neuronale in probleme de control si de modulare a sistemelor.......................24
6.2. Prelucrari de imagini cu retele neuronale.........25
6.3. Sistem expert cu retea neuronala multistrat.....
In retelele neuronale informatia nu mai este memorata in zone bine precizate, ca in cazul calculatoarelor standard, ci este memorata difuz in toata reteaua. Memorarea se face stabilind valori corespunzatoare ale ponderilor conexiunilor sinaptice dintre neuronii retelei.
Un alt element important, care este, probabil, principalul responsabil pentru succesul modelelor conexioniste, este capacitatea retelelor neuronale de a invata din exemple. In mod traditional, pentru a rezolva o problema, trebuie sa elaboram un model (matematic, logic, lingvistic etc.) al acesteia. Apoi, pornind de la acest model, trebuie sa indicam o succesiune de operatii reprezentand algoritmul de rezolvare a problemei. Exista, insa, probleme practice de mare complexitate pentru care stabilirea unui algoritm, fie el si unul aproximativ, este dificila sau chiar imposibila.
In acest caz, problema nu poate fi abordata folosind un calculator traditional, indiferent de resursele de memorie si timp de calcul disponibil.
Caracteristic retelelor neuronale este faptul ca, pornind de la o multime de exemple, ele sunt capabile sa sintetizeze in mod implicit un anumit model al problemei.
Se poate spune ca o retea neuronala construieste singura algoritmul pentru rezolvarea unei probleme, daca ii furnizam o multime reprezentativa de cazuri particulare (exemple de instruire).
Capitolul 1 are un caracter introductiv si schiteaza ideile de baza ale calculului neuronal.
In Capitolul 2 se prezinta elementele fundamentale privind arhitectura si functionarea retelelor neuronale. Se da ecuatia generala a evolutiei unei retele neuronale si se prezinta cinci modele fundamentale ale instruirii acestor retele.
Capitolul 3 prezinta studiul perceptronului si diferitelor sale variante. Perceptronul standard este un model simplu de retea neuronala iar functionarea se bazeaza pe algoritmul de instruire.
Perceptronul multi strat este o retea neuronala avand o arhitectura formata din mai multe straturi succesive de neuroni simpli.
Capitolul 4 arata modul de instruire a retelelor multi strat prin metoda de propagare inapoi a erorii. Se prezinta diferite metode care algoritmul de propagare inapoi.
Capitolul 5 ne prezinta arhitecturi moderne de retele neuronale si a unor metode evolutive de optimizare bazate pe algoritmi evolutivi.
Capitolul 6 este dedicat aplicatiilor calculului neuronal. Aplicatiile retelelor neuronale sunt numeroase si acopera o arie larga de domenii. Printre aplicatiile calculului neuronal se numara optimizare combinatoriala, probleme de control si modelare a unor sisteme complexe, prelucrarea imaginilor si recunoasterea formelor.
Procese de invatare in sisteme cu inteligenta artificiala
Inteligenta artificiala, ca si in cazul inteligentei biologice se dobandeste printr-un proces continu si de durata de invatare, de aceea problema invatarii ocupa un loc important in cercetarea masinilor auto-instruibile (machine learning).
Prin invatarea automata se intelege studiul sistemelor capabile sa-si imbunatateasca performantele, utilizand o multime de date de instruire.
Sistemele cu inteligenta artificiala obisnuite au capacitati de invatare foarte reduse sau nu au de loc. In cazul acestor sisteme cunoasterea trebuie sa fie programata in interiorul lor. Daca sistemele contin o eroare ,ele nu o vor putea corecta, indiferent de cate ori se executa procedura respectiva. Practic aceste sisteme nu-si pot imbunatatii performantele prin experienta si nici nu pot invata cunostinte specifice domeniului, prin experimentare. Aproape toate sistemele cu inteligenta artificiala sunt sisteme deductive. Aceste sisteme pot trage concluzii din cunoasterea incorporata sau furnizata, dar ele nu pot sa genereze singure noi cunostinte.
Pe masura ce un sistem cu inteligenta artificiala are de rezolvat sarcini mai complexe, creste si cunoasterea ce trebuie reprezentata in el (fapte, reguli, teorii). In general un sistem functioneaza bine, in concordanta cu scopul fixat prin cunoasterea furnizata, dar orice miscare in afara competentei sale face ca performantele lui sa scada rapid. Acest fenomen este numit si fragilitatea cunoasterii.
Una din directiile de cercetare in privita masinilor instruibile este modelarea neuronala . Modelarea neuronala dezvolta sisteme instruibile pentru scopuri generale, care pornesc cu o cantitate mica de cunostinte initiale. Astfel de sisteme se numesc retele neuronale sisteme cu auto-organizare sau sisteme conexioniste.
Un sistem de acest tip consta dintr-o retea de elemente interconectate de tip neuron, care realizeaza anumite functii logice simple.
Un astfel de sistem invata prin modificarea intensitatii de conexiune dintre elemente, adica schimband ponderile asociate acestor conexiuni. Cunoasterea initiala ce este furnizata sistemului este reprezentata de caracteristicile obiectelor considerate si de o configuratie initiala a retelei.
Sistemul invata construind o reprezentare simbolica a unei multimi date de concepte prin analiza conceptelor si contraexemplelor acestor concepte. Aceasta reprezentare poate fi sub forma de expresii logice, arbori de decizie, reguli de productie sau retele semantice.
Istoria Retelelor Neuronale Artificiale (RNA) sau, simplu, a Retelelor Neuronale incepe cu modelul de neuron propus de catre McCulloch si Pitts (un logician si un neurobiolog) in 1943. si este numit acest model neuronal, neuronul MP.
Modelul MP presupune ca neuronul functioneaza ca un dispozitiv simplu, ale carui intrari sunt ponderate. Ponderile pozitive sunt excitatoare iar ponderile negative sunt inhibitoare. Daca excitatia totala, adica suma ponderata a intrarilor, depaseste un anumit prag, atunci neuronul este activat si emite un semnal de iesire (iesirea are valoarea +1). Daca excitatia totala este mai mica decat valoarea prag, atunci neuronul nu este activat si iesirea lui se considera a fi zero.
Hebb (1949) a propus un mecanism calitativ ce descrie procesul prin care conexiunile sinaptice sunt modificate pentru a reflecta mecanismul de invatare realizat de neuronii interconectati atunci cand acestia sunt influentati de anumiti stimuli ai mediului.
Rosenblatt (1958 1959) a propus un dispozitiv numit perceptron. Perceptronul este bazat pe interconectarea unei multimi de neuroni artificial si reprezinta primul model de retea neuronala artificiala
Bernard Widrow a propus un model neuronal numit ADALINE si o retea cu elemente de acest tip numit MADALINE. ADALINE reprezinta acronimul ADAptive Linear Neuron sau ADAptive LINear Element. MADALINE este un acronim pentru Multiple-ADALINE.
Modelul ADALINE este in esenta identic cu modelul perceptronului. Iesirea este bipolara: +1 sau -1.ADALINE este un dispozitiv adaptiv, in sensul ca exista o procedura bine definita de modificare a ponderilor pentru a permite dispozitivului sa dea raspunsuri corecte pentru o intrare data.
Retelele neuronale permit rezolvarea unor probleme complicate, pentru care nu avem un algoritm secvential dar posedam unele exemple de solutii. Invatand din aceste exemple (faza de instruire), reteaua va fi capabila sa trateze cazuri similare (faza de lucru).
Calculatoarele obisnuite sunt, desigur, instrumente extrem de adecvate in rezolvarea unui spectru larg de probleme matematice, stiintifice, ingineresti. Calculatoarele isi dovedesc limitele in domenii in care omul exceleaza, cum ar fi perceptia si invatarea din experienta.
Intr-un calculator obisnuit elementul esential este procesorul, caracterizat de viteza mare de lucru. In creier, elementele individuale de proces sunt celulele nervoase (neuronii). Ele sunt mai simple si mai lente decat un procesor de calculator, insa sunt foarte numeroase. Conexiunile dintre neuroni sunt la fel de importante ca si acestia. Inteligenta si procesele memoriei rezida in intreaga retea de celule si nu in neuronii individuali.
Cortexul cerebral este o retea neuronala naturala .O astfel de retea neuronala are capacitatea de a gindi, invata, simti si de a-si aminti.
Retelele neuronale artificiale sunt retele de modele de neuroni conectati prin intermediul unor sinapse ajustabile. Toate modelele de retele neuronale se bazeaza pe interconectarea unor elemente simple de calcul dintr-o retea densa de conexiuni.
Fiecare unitate de proces este capabila sa execute doar calcule simple, dar reteaua, ca intreg, poate avea calitati remarcabile in recunoasterea formelor, rezolvarea problemelor pentru care nu posedam un algoritm, invatarea din exemple sau din experienta.
Paralelismul inalt si capacitatea de invatare reprezinta caracteristicile fundamentale ale retelelor neuronale
Calcululul neuronal implica doua aspecte fundamentale: invatarea si reprezentarea cunoasterii.
Retelele neuronale achizitioneaza cunoasterea prin instruire.
O retea neuronala este instruita daca aplicarea unei multimi de vectori de intrare va produce iesirile dorite. Cunoasterea pe care reteaua neuronala o dobandeste este memorata de sinapsele neuronale, mai precis, in ponderile conexiunilor dintre neuroni.
Multi dintre algoritmi de instruire pot fi considerati ca avandu-si originea in modelul de invatare propus de catre Donald Hebb(1949). Donald propune un model al schimbarilor conexiunilor sinaptice dintre celulele nervoase. Conform modelului lui Hebb, intensitatea conexiunii sinaptice dintre doi neuroni (ponderea conexiunii) creste de cate ori acesti neuroni sunt activati simultan de un stimul al mediului. Acest mecanism este cunoscut de regula lui Hebb de invatare.
Daca yi este activarea neuronului i si exista o legatura sinaptica intre neuroni i si j, atunci, in concordanta cu legea lui Hebb, intensitatea conexiunii lor sinaptice este afectata de:
Dwij=c yi yj,
unde c este un coeficient de proportionalitate adecvat ce reprezinta constanta de instruire. Aceasta lege apare ca naturala in multi algoritmi de invatare. In plus, exista argumente neuro-biologice care sprijina ipoteza ca stimulii mediului cauzeaza modificari sinaptice.
Acest mecanism este un model de invatare nesupervizata in care drumurile neuronale des utilizate sunt intensificate (intarite). Acest model poate explica fenomenele de obisnuinta si de invatare prin repetare.
O retea neuronala artificiala care foloseste o invatare hebbiana va determina o crestere a ponderilor retelei cu o cantitate proportionala cu produsul nivelurilor de exercitare neuronale.
Fie wij(n) ponderea conexiunii de la neuronul i la neuronul j inainte de ajustare si wij(n+1) ponderea acestei conexiuni dupa ajustare. Legea Hebb de invatare se va scrie in acest caz sub forma:
wij(n+1) = wij(n) + c yi yj ,
unde yi este iesirea neuronului i (intrarea neuronului j) iar yj este iesirea neuronului j.
O varianta a acestei legi de invatare este legea hebbiana a semnalului. In concordanta cu aceasta lege modificarea ponderilor este data de:
wij(n+1) = wij(n) + c S(yi) S(yi) ,
unde S este o functie sigmodala.
Un alt tip de invatare este invatarea competitiva. In acest caz, mai multi neuroni concureaza la privilegiul de a-si modifica ponderile conexiunilor, adica de a fi activati.
Elemente de neurodinamica
MODELUL GENERAL AL UNEI RETELE NEURONALE
In concordanta cu capitolul precedent vom admite ca o retea neuronala (RN) consta dintr-o multime de elemente de prelucrare (neuroni, unitati cognitive au noduri ale retelei) inalt interconectate.
Consideram in continuare o retea cu p neuroni. Acestia sunt conectati printr-o multime de ponderi de conexiune sau ponderi sinaptice. Fiecare neuron i are ni intrari si o iesire yi. Intrarile reprezinta semnale venite de la alti neuroni sau din lumea exterioara.
Intrarile xi ale neuronului i se reprezinta prin numerele reale x1i, xni. Fiecare neuron i are ni ponderi sinaptice, una pentru fiecare intrare a sa. Aceste ponderi se noteaza cu w1i, w2i,, wni si reprezinta numere reale care pondereaza semnalul de intrare corespunzator.
Daca wij > 0 avem o pondere sinaptica excitatoare iar daca wij < 0 avem de-a face cu o pondere inhibitoare. Pentru simplitate, in cele ce urmeaza se va suprima indicele i.
Fiecare neuron calculeaza starea sa interna sau activarea (excitatia) totala ;ca fiind suma ponderata; a semnalelor de intrare.
Notand cu s activarea, avem
n
j=1
In modelul McCulloch-Pitts fiecare neuron este caracterizat de un prag de excitare. Vom nota acest prag cu t. iesirea y a neuronului este +1 daca activarea totala este egala sau mai mare decat t.
Daca f : R - R este functia de raspuns definita prin:
![]()
1, daca x
F(x)=
0, daca x <
atunci iesirea neuronului se scrie ca
y=f(awj xj+t).
Valoarea prag t poate fi eliminata din argumentul functiei f daca se adauga neuronului un semnal de intrare care are intotdeauna valoarea 1 si ponderea t, adica
xn+1 = 1
iar
wn+1 = t
In acest caz activarea totala este
n+1
s awj xj
j=1
si iesirea se poate scrie
y = f(s
Avantajul acestei abordari este acela ca pragul poate fi ajustat impreuna cu celelalte ponderi in timpul procesului de instruire. Modelul neuronal considerat se poate reprezenta schematic ca in Figura 1.
![]()
![]()
![]()
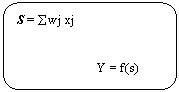 x1 w1
x1 w1
x2 w2
![]()
![]() y
y
![]()
![]() xn wn
xn wn
Figura 1. Modelul neuronal McCulloch-Pitts
Forma functiei de raspuns f depinde de modelul de retea neuronala studiat. Aceasta functie se mai numeste functie neuronala, functie de iesire sau functie de activare a neuronului. In general, se considera functii neuronale neliniare.
Se prezinta cateva functii neuronale ce reprezinta diferite tipuri de neliniaritate
functia prag asociata modelului McCulloch-Pitts este functia f R avand forma
![]()
1, daca x
F(x)=
0, daca x <
functia signum, f R
![]()
1, daca x
F(x)=
-1, daca x <
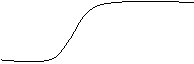
functie de tip sigmoidala f R f(x)=1+1 e-kx ,k >
![]()
 1 f(x)
1 f(x)
![]()
![]() X
X
Figura 2 Graficul unei functii sigmoidale
Functiile sigmoidale reprezinta forme netezite ale functiei prag liniare. Toate aceste functii sunt continue, derivabile si monoton crescatoare. Aceste proprietati sunt foarte convenabile pentru aplicatii. Observam ca functiile sigmoidale, ca si cele cu prag liniar, pot produce si valori de iesire intermediare celor doua valori extreme (0 si 1). Acest lucru reprezinta o facilitate pentru calculul analogic si pentru modelarea unei logici multivalente.
RETELE NEURONALE MULTISTRAT
Neuronii pot fi conectati in diferite moduri pentru a forma o retea '
neuronala. Un model uzual de topologie considera neuronii organizati in mai multe straturi.
O retea neuronala multistrat contine doua sau mai multe straturi de neuroni. Primul strat primeste intrarile din mediu. Iesirile neuronilor din acest strat constituie intrari pentru neuronii stratului urmator. Iesirea retelei este formata din iesirile neuronilor ultimului strat. Straturile situate intre primul si ultimul nivel sunt straturi ascunse ale retelei. Schema unei astfel de topologii este data in Figura 3.
Motivul acestei complicari a arhitecturii este legat de faptul ca, uneori, arhitecturile mai simple se dovedesc incapabile de a rezolva o problema sau o clasa de probleme. Daca o retea data nu poate rezolva o problema, este uneori suficient sa marim numarul neuronilor din retea. pastrand vechea arhitectura. In alte situatii, pentru rezolvarea problemei este necesar sa modificam arhitectura retelei, introducand unul sau mai multe straturi neuronale noi.
![]()
![]()
![]()
![]() X Y
X Y
![]()
![]()
![]()


![]()



![]()

![]()

![]()

![]()
![]()
![]() x1 y1
x1 y1

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() intrari iesiri
intrari iesiri
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() xn yn
xn yn
Figura 3 O retea cu doua straturi ascunse
In reteaua din Figura 3 nu exista conexiuni intre neuronii aceluiasi strat. Semnalul se propaga in retea dinspre stratul de intrare spre cel de iesire. Spunem ca avem o propagare inainte a semnalului in retea (retea cu transmitere inainte a semnalului).
. Putem astfel considera arhitecturi de retea in care exista conexiuni intre neuronii aceluiasi strat. De asemenea, uneori poate fi util sa consideram conexiuni de la un neuron spre neuroni aflati in stratul anterior (mai apropiat de intrarea retelei). Alteori, conexiunile pot lega doi neuroni care nu se afla neaparat in straturi adiacente.
3. Modelul Perceptronului
Modelul perceptronului reprezinta samburele din care s-au dezvoltat toate celelalte retele neuronale.
Arhitectura perceptronului standard este cea mai simpla configuratie posibila a unei retele si ea permite ca instruirea acesteia sa se realizeze folosind un algoritm simplu si eficient.
Algoritmul este reprezentat de o clasa larga de algoritmi de instruire, vectorii din multimea de instruire se reprezinta retelei impreuna cu clasa careia ii apartin. Daca au fost memorate suficient de multe obiecte din fiecare clasa, se poate construi o reprezentare interna a fiecarei clase prin ponderile de conexiune ale retelei.
PERCEPTRONUL CU UN SINGUR STRAT
Perceptronul cu un singur strat este cea mai simpla retea neuronala.
Valorile de intrare pot fi binare sau numere reale. Aceasta retea elementara are capacitatea de a invata sa recunoasca forme simple.
Un perceptron este capabil sa decida daca un vector de intrare apartine uneia din cele doua clase de instruire, notate cu A1 si A2.
![]()
![]() x1 t
x1 t
 w1
w1
![]() y
y
![]() wn
wn
xn
Figura 4. Perceptronul cu un singur strat
Acest perceptron este implementat cu un singur neuron. Daca x este vectorul ce reprezinta intrarile neuronului, putem calcula suma ponderata a elementelor de intrare.
![]()
![]()
x1
X= x2 , xj I R
xn
s = a wI xI
Admitand ca perceptronul are iesirile -1 si +1. Iesirea y este data de urmatoarea regula
s > -t T y = 1,
s < -t T y = -1,
unde t este un prag al neuronului. Iesirea y = 1 corespunde faptului ca vectorul de intrare apartine clasei A1. Daca iesirea este -1 atunci vectorul prezentat retelei apartine clasei A2
Notand cu x vectorul de intrare extins,
![]()
![]()
x1
.
x .
xn
si cu v vectorul ponderilor la care adaugam o componenta cu pragul t,
![]()
![]()
w1
v = . .
wn
t
Cu aceste notatii iesirea perceptronului este data de regula
vTx > T y = +1
vTx < T y = -1
Ponderile conexinilor si pragul (componentele vectorului v) unui perceptron se pot adapta folosind un algoritm de instruire simplu numit algoritmul perceptronului.
ALGORITMUL DE INSTRUIRE
Se va prezenta algoritmul standard pentru instruirea perceptronului cu doua clase de instruire.
La primul pas al algoritmului de instruire se initializeaza valorile ponderilor si pragul. Ponderile initiale sunt componentele vectorului v1. Se aleg pentru ponderile initiale numere reale mici si nenule. Se alege valoarea constantei de corectie c (de obicei 0 < c
Constanta c controleaza rata de adaptare a retelei. Alegerea ei trebuie sa satisfaca cerinte contradictorii: pe de o parte exista necesitatea de a obtine o adaptare rapida a ponderilor la intrari si pe de alta parte trebuie sa se tina seama de necesitatea ca medierea intrarilor precedente sa genereze o estimare stabila a ponderilor.
Algoritmul de invatare al perceptronului compara iesirea produsa de retea cu clasa corespunzatoare a vectorului de intrare. Daca s-a produs o clasificare eronata, atunci vectorul pondere este modificat. In caz contrar el ramane neschimbat.
Daca la p pasi consecutivi nu se produce nici o modificare a vectorului pondere, atunci toti vectorii (formele) de instruire sunt corect clasificati de ultimul vector ponderere rezultat. Am obtinut un vector solutie si algoritmul se opreste cu aceasta decizie. Procedura de instruire descrisa mai sus conduce la algoritmul urmator pentru instruirea perceptronului :
ALGORITMUL PERCEPTRONULUI
P1 Se initializeaza ponderile si pragul.
Se aleg componentele w1,.., wn si t ale vectorului v1.
Se pune k = 1 (v1 este vectorul pondere la momentul initial).
P2 Se alege constanta de corectie c >
P3 Se alege o noua forma de instruire.
Se reprezinta retelei o noua forma de intrare zk si iesirea dorita, (asteptata) corespunzatoare.
P4 Se calculeaza iesirea reala generata de perceptron. Iesirea reala este data de semnul expresiei (vk)T zk.
P5 Conditia de oprire.
Se repeta pasul P6 pana cand vectorul pondere nu se modifica la p pasi consecutivi.
P6 Se adapteaza ponderile si pragul.
Se modifica vectorul pondere folosind regula de corectie
![]()
vk +czk , daca (vk)Tzk
vk, daca (vk)Tzk >
Se pune k = k + 1.
Daca algoritmul s-a oprit normal, atunci vectorul vk+1 reprezinta o solutie a problemei de instruire .
LIMITELE PERCETRONULUI
In multe probleme concrete de clasificare si de instruire intervin clase de obiecte care nu sunt liniar separabile. Deoarece perceptronul nu poate discrimina decat clase liniar separabile, aplicarea acestui algoritm in rezolvarea unor probleme concrete este sever limitata.
Cea mai celebra si una dintre cele mai simple probleme care nu pot fi rezolvate de un perceptron este, problema calcularii valorilor functiei logice sau exclusiv
Problema poate fi rezolvata de un perceptron cu mai multe straturi,(cu doua straturi).
Aceasta limitare, nu se datoreaza algoritmului, ci este legata de topologia foarte simpla retelei utilizate. Daca problema de instruire necesita regiuni de decizie mai complicate, atunci trebuie marita complexitatea retelei.
4. Propagarea inapoi a erorii
Algoritmul de propagare inapoi (Back Propagation) este considerat in mod uzual, ca fiind cel mai important si mai utilizat algoritm pentru instruirea retelelor neuronale.
Algoritmul de propagare inapoi este o metoda de instruire in retelele neuronale multistrat cu transmitere inainte (retele unidirectionale), in care se urmareste minimizarea erorii medii patratice printr-o metoda de gradient.
Caracteristica esentiala a retelelor cu doua straturi este ca ele proiecteaza forme de intrare similare in forme de iesire similare fapt ce permite sa faca generalizarile rezonabile si sa prelucreze acceptabil forme care nu li s-au mai prezentat niciodata.
FUNCTIA CRITERIU
Tehnica de instruire descrisa mai jos este asemanatoare cu cea utilizata pentru a gasi dreapta care aproximeaza cel mai bine o multime data de puncte (problema regresiei). Aceasta tehnica este o generalizare a metodei MEP. Pentru determinarea dreptei de regresiei, se utilizeaza, de regula, metoda celor mai mici patrate. Deoarece este plauzibil ca functia pe care o cautam sa fie neliniara, se foloseste o varianta iterativa a metodei celor mai mici patrate.
Fie f Rn Rp functia necunoscuta pe care reteaua trebuie sa invete (sa o realizeze). Vectorul de intrare xi ii corespunde raspunsul dorit di .
di = f(xi).
La momentul k, retelei i se reprezinta asocierea vectoriala (xk, dk). Admitand ca multimea de instruire e formata din m asocieri,
(x1,d1), . ,(xm,dm).
Starea curenta (la momentul k) a retelei neuronale defineste functia vectoriala
Nk Rn Rp
Unde y este vectorul care indica activarea neuronilor ultimului strat al retelei.
![]()
![]()
y1
y = .
yp
Daca S este functia vectoriala de iesire, atunci, la momentul k, reteaua genereaza raspunsul S(yk). Iesirea vectoriala a retelei este,asadar
Nk(xk) = S(yk).
Fie Sj R R functia de raspuns a neuronului j din stratul final. Functiile S1,.., Sp sunt marginite si crescatoare.
Se poate scrie deci sub forma
![]()
![]()
S1(y1k)
Nk(xk) =
Sp(ypk)
Algoritmul de propagare inapoi cere ca functiile de raspuns sa fie derivabile. Aceasta conditie elimina posibilitatea utilizarii functiilor cu prag liniar, nederivabile in punctele prag. Rezulta, deci, ca se poate folosii functia sigmoidala sau functia identica. O functie de raspuns liniara defineste un neuron de iesire liniar.
Iesirea reala a neuronului de iesire j, cand la intrare se prezinta vectorul xk este
ojk = Sjo(yjk),
unde indicele o desemneaza iesirea.
Eroarea corespunzatoare neuronului j cand retelei i se furnizeaza vectorul xk este
ejk = djk - ojk
= djk- Sjo(yjk).
Eroarea patratica a tuturor neuronilor de iesire in raport cu intrarea xk se defineste ca
Ek = 1 a(ejk)2
Eroarea patratica se mai poate scrie
Ek = 1 2(ek)Tek.
Eroarea totala este suma erorilor pentru cele m asocieri din multimea de invatare m
E = aEk
K = 1
unde m este numarul de forme din aceasta multime.
Algoritmul de propagare inapoi urmareste minimizarea erorii patratice, insa nu este sigur ca algoritmul gasit va minimiza si aceasta functie criteriu. Ceea ce se obtine este, in general, o solutie acceptabila si nu, neaparat, o solutie optima.
4.2. ALGORITMUL DE PROPAGARE INAPOI
Aplicarea algoritmului de propagare inapoi presupune doua etape. In prima etapa se prezinta retelei un vector de intrare xk si iesirea dorita corespunzatoare .
Fie dk aceasta iesire, semnalul de intrare se propaga prin retea si genereaza un raspuns. Neuronul j din campul de iesire produce semnalul
ojk = Sjo(yjk).
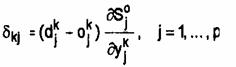
Figura . Unitatea formei Acest semnal este comparat cu raspunsul dorit djk
.Rezulta un semnal de eroare dkj care se
calculeaza pentru fiecare neuron de iesire
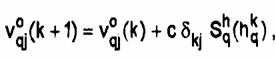
Se
calculeaza schimbarile ponderilor pentru toate conexiunile ce
intra in stratul final, folosind regula urmatoare
unde Sqh(hqh)este iesirea neuronului ascuns q.
Cea de a doua faza a algoritmului corespunde propagarii inapoi prin retea a semnalului de eroare. Aceasta permite calculul recursiv al erorii conform formulei.
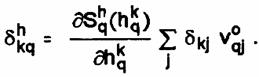
Calculul se face pentru fiecare neuron q din stratul ascuns. Altfel, eroarea se propaga inapoi prin retea. Propagarea inapoi implica un calcul de aceeasi complexitate cu propagarea inainte a semnalului si nu necesita un efort excesiv de timp si memorie.
Arhitecturi moderne de retele neuronale
In acest capitol sunt prezentate doua din cele mai noi arhitecturi de retele neuronale, retele cu eficienta crescuta, aparute din nevoia de a inlatura unele neajunsuri ale modelelor clasice (ex. perceptronul multistrat)
RETELE NEURONALE PROBABILISTICE
Modelarea retelelor neuronale cu ajutorul teoriei probabilitatilor sau a teoriilor de incertitudine aduce o serie de avantaje fata de abordarile strict deterministe. Acestea sunt:
- reprezentarea mai veridica a modului de functionare a retelelor neuronale biologice, in care semnalele se transmit mai ales ca impulsuri;
- eficienta de calcul mult superioara celei din cadrul retelelor neuronale ,inainte-inapoi';
-implementare hardware simpla pentru structuri paralele;
- instruire usoara si cvasiinstantanee, rezultand posibilitatea folosirii acestor retele neuronale in timp real;
- forma suprafetelor de decizie poate fi oricat de complexa prin modificarea unui singur parametru (de netezire) s, aceste suprafete putand aproxima optim suprafetele Bayes;
- pentru statistici variabile in timp, noile forme pot fi suprapuse simplu peste cele vechi;
~ comportare buna la forme de intrare cu zgomot sau incomplete.
Astfel, pentru o problema biclasa, consideram o retea neuronala probabilistica in care stratul numit ,unitati ale formei contine elemente avand structura din figura .
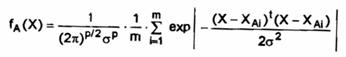
Pentru o distributie normala a densitatii de
probabilitate, estimatorul pentru clasa A este
functie ce apare la iesirea unitatii formei, unde X W. Unitatile sumatoare aduna datele de la unitatile formei ce corespund multimii de instruire si au o pondere variabila, Ck ,(Figura ).
Ponderea Ck este data de
Ck = -(hBk IBk) (hAk IAk) nAk nBk
unde nAk si nBk sunt numarul formelor de antrenare pentru clasa Ak respectiv Bk , h sunt probabilitatile a priori, I sunt functii de pierdere in cazul unei decizii eronate iar THR (Figura ) este functia prag.
Instruirea consta in identitatea dintre vectorul Wi si fiecare forma de antrenare x. Astfel, este necesara cate o unitate pentru fiecare forma din multimea de instruire.
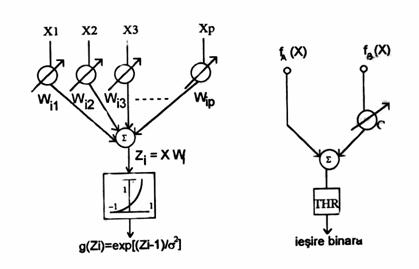
Figura 5. Unitatea formei Figura 6. Neuron sumator
RETELE NEURONALE FUZZY
Combinarea celor doua clase de sisteme cognitive nuantate (fuzzy) si neuronale, s-a impus prin performantele bune, de cativa ani.
Fuzzyficarea arhitecturilor neuronale mareste capacitatea retelelor neuronale de a recunoaste (clasifica) forme complexe, distorsionate sau incomplete.
O structura de retea neuronala a fost propusa de catre Watanabe . Acest model foloseste neuronul logic(Figura 7).
Neuronul logic are avantajul vitezei si al unei capacitati discriminatorii remarcabile (pragul fiind independent de marimea in biti a componentelor vectorului de intrare). Acum avem doua tipuri de vectori pondere
Wp = (Wp1 ,..., Wpn)
si
Wn = (Wn1 ,..., Wnn)
Raspunsul analog y, ce urmeaza a fi cuantizat, are forma
y = (xi ai
xI fiind intrarile. Iesirea binara a sistemului este
z = SGN(y-h),
unde h este pragul fixat.
Vectorul pondere este ajustat dupa diferenta e intre iesirea dorita si raspunsul sistemului la diferite intrari in cursul instruirii iar h se calculeaza cu operatii logice fuzzy
ht = ( Wpi) (wni)
hB = (Wpi) (Wni)
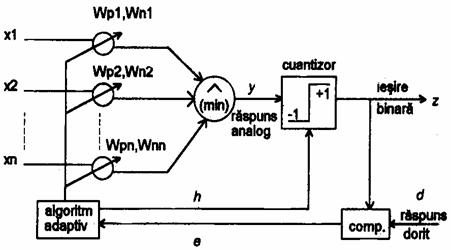
h = hT +
hB
Figura 7. Configuratia unui neuron logic tip ADN
6. Aplicatii ale Retelelor Neuronale
6.1. RETELE NEURONALE IN PROBLEME DE CONTROL SI DE MODULARE A SISTEMELOR
Controlul automat si modelarea sistemelor dinamice (liniare sau neliniare) constitue o aplicatie majora a retelelor neuronale. Este cunoscut faptul ca un sistem dinamic este descris de ecuatii diferentiale care, in functie de complexitatea sistemului, au adesea o rezolvare laborioasa.
Desi majoritatea retelelor neuronale sunt statice, un proces dinamic poate fi modelat in timp discret oferind retelei exemple de instruire constand in intrari si iesiri trecute ale procesului. Reteaua este capabila sa invete transformarea neliniara f, unde
y(k)=f(x) , x = [u(k-1), u(k-2),., u(k-nu),y(k-2),., y(k-ny)]T ,
in care x(u) si y sunt, respectiv, intrarea si iesirea sistemului. Ordinele dinamice nu si ny ale sistemului trebuie sa fie cunoscute a priori sau trebuie estimate din setul se date.
Problema identificarii sistemului neliniar implica atat estimarea cat si aproximarea erorilor. In cazul proceselor liniar, functia devine hiperplanul
y(k)=b1u(k-1)+b2u(k-2)+.+bnuu(k-nu) - a1y(k-1)-a2y(k-2).-anyy(k-ny).
Descrierea completa a sistemului este data de gasirea pantelor (-ai) si bi.
arctan(1)![]()

![]()
![]()
![]() 0.1903 z-1
0.1903 z-1
1- 0.9048 z-1
u y
Figura. 8. Proces dinamic de ordinul unu
O modelare eficienta a sistemului de mai sus consta intr-o combinatie de optimizare liniara si una neliniara. O prima abordare porneste cu alegerea centrilor si a dispersiei prin metoda neliniara a perceptronului multistrat, urmata de calcululul ponderilor prin optimizare liniara (metoda matricei pseudo-inverse). A doua cale foloseste mai intai optimizarea liniara obisnuita a centrilor, a dispersiei σ si a ponderilor, dupa care algoritmul perceptronului va produce o acordare fina a solutiei obtinute.
Algoritmul combinat de optimizare este urmatorul:
Selectia centrilor si a dispersiei prin grupare, folosind metoda celui mai apropiat vecin.
Optimizarea liniara a ponderilor.
Daca performantele sunt satisfacatoare, stop. Daca nu, se continua cu parametri initiali ai retelei.
Reactualizarea centrilor si a dispersiei prin optimizarea neliniara.
Optimizarea liniara a ponderilor.
Se merge la pasul 4 pana la obtinerea convergentei in timpul minim.
6.2. PRELUCRARI DE IMAGINI CU RETELE NEURONALE
Proprietatile de baza ale retelelor neuronale, anume faptul ca sunt aproximatori universali si ca au o capacitate de predictie deosebita, isi gasesc utilizarea imediata in cadrul altor domenii, cum ar fi prelucrarea de imagini, recunoasterea formelor vizuale scris si amprente sau recunoasterea vorbirii.
Filtrarea zgomotelor, accentuarea si detectia contururilor, segmentarea imaginii si extragerea caracteristicilor sunt cele mai importante operatii de procesare. Desi metodele clasice de prelucrare satisfac majoritatea aplicatiilor exista tehnici hibride de tipul segmentare clasificare, pentru care metodele conexioniste ofera performante superioare in raport cu rata de recunoastere si cu timpul de calcul.
Implementarea se poate realiza cu retele neuronale celulare, care sunt circuite analogice neliniare ce permit o implementare VLSI, retelele celulare putand efectua prelucrari paralele de semnal in timp real. Ecuatia de iesire a unui nod oarecare reprezinta un filtru bidimensional, neliniar si invariant in spatiu.
O aplicatie foarte utila este recunoasterea on line a semnaturilor grafologice cu ajutorul unui neurocalculator. Se pot folosi drept caracteristici coordonatele planare si presiunea stiloului, extrase cu ajutorul unei tabele grafice. Sunt luate in consideratie variabilitatea semnaturilor corecte, precum si semnaturile false.
6.3. SISTEM EXPERT CU RETEA NEURONALA MULTISTRAT
O arhitectura reprezentativa de sistem expert bazat pe o retea neuronala . multistrat instruita cu algoritmul propagarii inverse a fost propusa in. Algoritmul de instruire accepta forme de instruire pe interval, ceea ce face posibila si invatarea cu intrari irelevante si iesiri posibile. Un utilizator al sistemului poate defini tipurile de intrari si iesiri (real, intreg, scalar, multime), ca si modul lor de codificare (virgula mobila, binar, unar).
Intrarile si iesirile expert
In proiectarea particulara a sistemelor expert, este necesar sa se aleaga intrarile si iesirile expert care vor gasi o rezolvare optima a problemei aplicative. diferite posibilitati de intrari si iesiri expert, astfel incat diferite moduri de codificare sa respecte necesitatile aplicatiilor particulare.
Sa consideram un sistem expert neuronal cu un numar de intrari (simptome) si iesiri (diagnostice). Acestea pot fi variabile de tip real (intreg), scalar cu valori definite de utilizator si multime. Un exemplu de sistem expert de diagnostic medical simplu poate avea urmatorii parametri:
INTRARI DURERE DE GAT scalar din (NU, DA)
TEMPERATURA real din [36, 42]
IESIRI: BOALA: scalar din (SANATOS, RECE, ANGINA, GRIPA)
INCAPACITATEA DE MUNCA: scalar din (NU, DA)
MEDICATIE: multime din (DROPSURI, ASPIRINA, PENICILINA)
Valorile intrarilor si iesirilor intr-un sistem expert neuronal sunt codificate de valori analogice ale straturilor neuronilor de intrare si iesire utilizand virgula flotanta, codurile binare si unare. Tipul real codificat binar este, de fapt, de tip intreg.
Codificarea in virgula flotanta necesita numai un neuron. In codificarea unara si binara exista, in general, mai multi neuroni cu doua stari (-1 si 1) conform definitiei de tip. Valoarea unui tip arbitrar este mai intai transformata la o valoare numerica denumita index. Evaluarea indexului este ilustrata in Tabelul 1, pentru valori de diferite tipuri, date pentru exemplul de mai sus.
|
Tip |
Valoare |
Index |
Virgul mobila |
Cod binar |
Cod unar |
|
Real |
|
|
|
|
|
|
Intreg |
|
|
|
|
|
|
Scalar |
gripa |
|
|
|
|
|
Multime |
Dropsuri penicinina |
|
|
|
|
Tabelul 1. Exemple de codificari
Un expert isi formuleaza cunostintele sub forma de exemple tipice de inferente. O inferenta este o pereche compusa dintr-un vector de intrari tipice si vectorul corespunzator al iesirilor obisnuite prin raspunsurile expertului la aceste intrari. De exemplu, in medicina, documentatia medicala despre pacienti poate fi luata ca baza pentru crearea unei multimi de exemple tipice de inferenta. In acest caz, intrarile corespund cu rezultatele examinarilor medicale si iesirile sunt diagnosticele ori recomandarile medicamentoase date de doctor. Pentru exemplul de la sectiunea 6.3. multimea exemplelor de inferenta poate lua urmatoarea forma:
)
[ (DA, 37.2), (ANGINA, DA, ) ), ,
[ (NU, necunoscut), (SANATOS, NU, ) ] }
Baza de cunostinte a sistemului expert neuronal propus este o retea neuronala multistrat. Apare, insa, problema codificarii valorilor irelevante si necunoscute ale intrarilor si iesirilor expert. Pentru a intelege importanta acestei probleme, sa consideram un sistem expert medical cu 50 de intrari reprezentand rezultatele tuturor examinarilor medicale. In caz particular, multe dintre acestea sunt irelevante pentru determinarea diagnosticului final (de exemplu, razele X nu sunt necesare in stadiul de diagnoza a anginei).
Pentru a rezolva aceasta problema de codificare, putem crea mai multe exemple de inferenta substituind toate valorile posibile pentru intrari si iesiri irelevante. Acest proces conduce, in general, la o cantitate mare de date si este dificil de realizat. De aceea vom generaliza neuronul clasic la un neuron interval Valoarea irelevanta sau chiar necunoscuta a unei intrari sau iesiri expert este codificata utilizand intregul interval de stare a neuronilor.
Fie [-1, 1] acest interval. Valoarea cunoscuta este codificata de un singur punct din interval dupa procedura de codificare descrisa anterior. In acest fel, obtinem multimea alcatuita din forme de instruire interval. Forma de instruire interval este compusa din vectorul starilor de intrare interval ale neuronului si din vectorul corespunzator al starilor interval de iesire. In exemplul nostru, utilizand . tipul natural de codificare, forma de instruire interval este:
aspirina
Functia neuronului interval
Se introduce predicatul FP cu neuronul ca parametru, care este adevarat daca si numai daca acest neuron este un neuron de iesire care codifica iesirea expert in virgula flotanta. In aceasta abordare, se iau in consideratie intrarile interval [aj, bj], jI i , ale neuronului i. Potentialul intern de interval [x; , y si starea intervalului [ai, bj (iesirea) pentru acest neuron sunt date de:
![]()
yi FP(i)
ai =
Si(xi) , in rest
si
![]()
yi EP(I)
bi =
Si(yi), in rest,
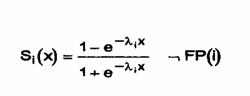
Unde
Algoritmul de instruire.
Se considera multimea de instruire
unde Ik este vectorul intervalelor de intrare si Ok este vectorul de iesire dorit corespunzator intervalelor de iesire ale retelei [Akv, Bkv], v indica neuronul de iesire relevant. Considerand [av(Ik), bv(Ik)] drept starea intervalului actual neuronului de iesire v pentru intrarea retelei Ik.
Definim functia de eroare partiala Ek drept o suma de diferente dintre iesirea dorita si cea actuala
Ek=1 a((av(Ik)-Akv)2+(bv(Ik)-Bkv)2).
Functia erorii totale E a retelei neuronale multistrat cu privire la intreaga multime de instruire este suma functiilor erorilor partiale
N
E=aEk.
K=1
Minimizarea erorii se face dupa metoda gradientului.
Dupa ce reteaua neuronala a fost construita se poate verifica daca baza de cunostinte neuronala creata este capabila sa deduca concluziile noastre. Verificarea poate fi facuta cu ajutorul unei multimi de test.
Bibliografie
***, " Curs de ingineria reglarii automate
Dumitrescu, D. "
Encarta Encyclopedi 1999