CIRCUITELE BISTABILE

CIRCUITE BISTABILE

1. Scopul lucrarii:

Cunoasterea modului de functionare si a configuratiei unor bistabile integrate, frecvent utilizate in circuite logice secventiale.

2. Consideratii teoretice:

Circuitul basculant bistabil CBB, este un circuit tipic cu doua stari distincte utilizat pentru pastrarea informatiei binare. Acesta prezinta doua conexiuni de intrare prin care accepta informatia binara care urmeaza a fi memorata, doua conexiuni de iesire care permit citirea starii bistabilului si in general, intrari suplimentare de control prin care se stabileste momentul in care informatia urmeaza a fi citita de bistabil. Cele doua iesiri ale unui bistabil sunt complementare. Trecerea intr-o anumita stare poate fi determinata fie de semnalul reprezentand informatia care trebuie inscrisa in bistabil, fie de semnalul de tact ce actioneaza in functie de starea intrarilor de informatie.

Semnalul de tact poate determina comutarea bistabilului in doua moduri: pe durata impulsului de tact, fiind deci precis definita in timp.

Proprietatea bistabilului de memorare a informatiei se manifesta prin faptul ca starea sa nu se schimba dupa disparitia semnalului de comutate.

3. Bistabilul asincron RS:

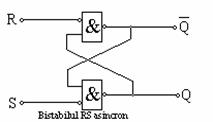
Bistabilul RS asincron, se obtine prin interconectarea a doua porti SI-NU in asa fel ca iesirile unuia sa fie conectate la intrarea celeilalte.

In functionarea normala nu se permite aplicarea simultana a semnalului logic "1" ape doua intrari R si deoarece conduce la prezenta semnalului logic "0" pe doua iesiri, situatie care este in contradictie cu data anterior privind caracterul complementar al iesirii unui bistabil.

4. Bistabilul sincron RS:

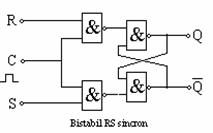Bistabilul RS sincron are schema in figura:

Ecuatiile logice caracteristice  sunt:; .

5. Bistabilul sincron D:

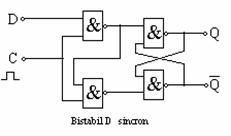
Bistabilul D sincron are schema in figura urmatoare, are o singura intrare:

Ecuatiile logice caracteristice sunt:; .

Deoarece pentru C=1, Q_t+1=D bistabilul se mai numeste si circuit elementar de intarziere in sensul ca semnalul aplicat la intrare se obtine la iesire cu intarzierea de un tact.

6. Bistabilul sincron JK:

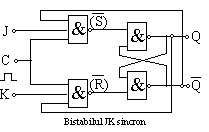
Bistabilul JK sincron are schema in figura urmatoare, realizata cu porti SI-NU :

Ecuatiile logice caracteristice sunt:; .

Prezinta neajunsul ca pentru a exista o singura basculare trebuie ca durata contactului de tact sa fie mai mare decat timpul de propagare printr-o poarta si mai mic decat timpul de propagare prin doua porti.

7. Bistabilul sincron T:

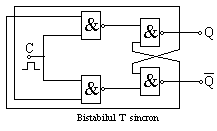Bistabilul T sincron are proprietatea de a-si schimba iesirea la fiecare impuls sosit la intrare. Acest efect poate fi obtinut realizand un bistabil care se autocomanda, schema in figura urmatoare:

Ecuatiile logice caracteristice sunt:; .

Odata ce bistabilul si-a schimbat starea si impulsul pe C persista, urmeaza o noua schimbare a starii, adica bistabilul oscileaza, fiind foarte dificil a determina starea sa finala, care depinde de raportul dintre durata impulsului pe intrarea C, si durata bascularii. Pentru a exista o singura basculare se impune pentru durata impulsului de tact aceeasi conditie ca si in cazul circuitului bistabil JK sincron.

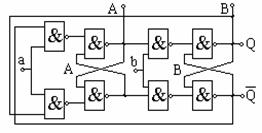
Pentru a rezolva deficienta sunt folosite 2 circuite de tip RS comandate prin impuls.

Primul, A, conditioneaza starea celui de-al doilea B, in timp ce al doilea , B, il conditioneaza pe primul, A.

Daca bistabilul A se afla in starea "1" la sosirea impulsului pe intrarea b, bistabilul B trece in starea "1", pe cand daca bistabilul B se afla in starea "1" la sosirea impulsului pe intrarea a, bistabilul A trece in starea "0".

Pentru o functionare corecta sunt necesare doua impulsuri a si b decalate in timp.

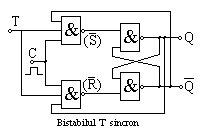
O alta schema logica a bistabilului T sincron cu porti SI-NU (NAND) este prezentata in figura alaturata.

Circuitul are proprietatea de a-si schimba starea la fiecare impuls de tact aplicat pe intrarea C, daca la intrarea T se aplica semnal logic "1".

Ecuatiile logice caracteristice sunt:; .

8. Mersul lucrarii:

Materiale si aparatura necesara: CI: CBD-400E, 410E (vezi anexa), stand pentru circuite integrate logice.

Modul de lucru:

a)     Se va realiza schema logica a bistabilului din figura, se verifica tabelul de adevar;

b)     Se va realiza schema logica a bistabilului RS sincron si se va verifica functionarea circuitului dupa tabelul de adevar in timp, stabilind conditiile logice pe S si R si aplicand impulsuri de tact;

c)     Se va realiza schema logica a bistabilului D si se testeaza tabelul de adevar din tabel;

d)     Se va realiza schema logica a bistabilului JK sincron si se va verifica functionarea circuitului dupa tabelul de adevar in timp, stabilind conditiile logice pe J si K si aplicand impulsuri de tact;

e)     Se va realiza schema logica a bistabilului T comandat prin doua impulsuri. Iesirile A si B se conecteaza la elementele de afisaj. Se aplica in mod succesiv impuls pe intrarea a si apoi pe intrarea b si se observa ca la fiecare sir de doua impulsuri bistabilul isi schimba starea.

9. Intrebari:

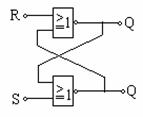
Sa se deduca ecuatiile logice si graful de tranzitii pentru bistabilul RS realizat cu NOR din figura urmatoare:

Sa se stabileasca daca tabelul de tranzitii si graful de tranzitii pentru bistabilul JK.

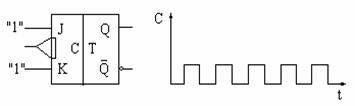Sa se deseneze formele de unda de la iesirea Q a bistabilului din figura urmatoare, la intrare aplicandu-se un tren de impulsuri TTL ca in figura.

Sa se demonstreze ca se poate obtine un circuit basculant bistabil T daca:

a.      se realizeaza conexiunile s→, respectiv R →Q ]n cazul unui circuit bistabil SR;

b.     se conecteaza intrarea D cu iesirea  la un circuit basculant bistabil D.