Research Practicum

Craciun Nicoleta Irina and Angelescu Cosmina

Assistant:

January 2004

Rijksuniversiteit Groningen

Nijengorgh 4

9747 AG Groningen

Laser Doppler Velocity Measurement

Abstract:

This experiment is to measure two flow profiles at laminar flow and one profile at turbulent flow and determine the flow velocity at the axis of the tube by applying Laser Doppler Velocimetry technique.

The three fluid velocities selected for the experiments are 1.8 m/s, 4.4 m/s and 46.3 m/s.

We will see that for the velocities m/s and m/s the flow profile is laminar and for the velocity of m/s the flow profile is turbulent.

Contents:

Introduction............................2

Theory ................................2

Experimental set-up...........................7

Result and discussions........................10

Conclusion...........................23

References............................23

Introduction

Laser Doppler Velocimetry (LDV) is a method for measuring the speed of small particles. When particles are suspended in a fluid in the presence of a known electric field, a velocity measurement is a measure of the mobility of the particles. Small particles suspended in fluid are illuminated by a laser beam and the light scattered to various angles is compared to light in a reference beam to determine the doppler shift of the scattered light. The doppler shift of the light depends on the speed of the particles and the angle of measurement. In this experiment LDV will be used to determine two profiles of laminar flow and one profile of turbulent flow [1].

2.Theory

2.1.a Hydrodynamics

In this experiment the flow profile in a straight cylindrical tube is to be measured. In such a tube two types of flow profiles can exist: a laminar flow and a turbulent flow. Which of the two will be encountered depends on the Reynolds number of the flow. The Reynolds number is given by [2,3]:

      (1)

                                               (2)

with the density of the fluid(/), R is radius of the tube(), 2R the inner diameter of the tube, the average velocity in the axial direction of the tube () and the absolute viscosity of the fluid () and is kinematics viscosity (). Reynolds number is a dimensionless quantity that characterises the flow. At low values of the Reynolds number () the flow will be laminar, at higher values () the flow will be turbulent.

Laminar Flow

Laminar flow is characterised by a situation in which the fluid particles flow in regular layers of different velocity. The flow is quite orderly. In a long cylindrical tube the flow velocity at distance r from the axis of the tube can be represented by [2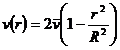,3]

                                 (3)

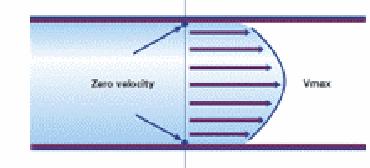
Figure1. Laminar flow profile [4].

Figure 1 shows that the velocity is zero at the solid wall of the tube and increases parabolically with flow, reaching its maximum at the centre of the tube in axis. At the axis of the tube the velocity of the fluid is given by . This is a useful criteria to see whether the flow is laminar or not.

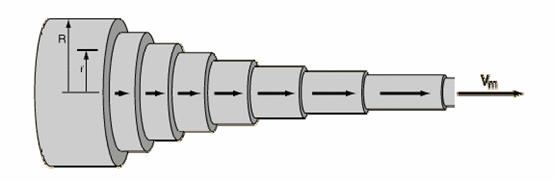
Figure2. Laminar flow profile in 3D perspective [5].

Turbulent Flow

At higher fluid velocities the order in the flow decreases; the fluid particles do not longer move straight lines through the tube, but there is momentum transfer in directions perpendicular to the axis of the tube. This results in a chaotic flow with

vertices that do not damp out. Turbulent flow is extremely complex. A complete theoretical description is still to be presented. However a description that is often used for the average flow profile is given by Nikoradze [2,6].

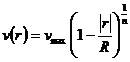     (4)

With the maximum velocity of the flow at the axis of the tube and the constant die represents the degree of turbulence [2].

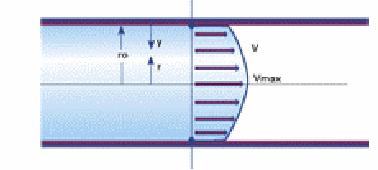
Figure 3. Turbulent flow profile [4].

Figure 3 shows at the turbulent flow velocity is zero at the solid wall of the tube, but the face velocity is straighter and squared up. As the velocity of the fluid continues to increase the face velocity will continue to straighten up until all particles are moving at the same velocity ( except at the solid wall of the tube where the flow remains at zero) [4].

Experimental values of n are 6 ( at ), 7 ( at ), or even n=10 at extremely high values of [6].

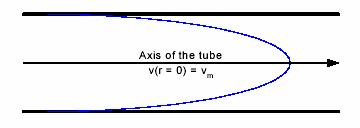
Figure 4. Turbulent flow profile according to the formula of Nikoradze.

For the description of turbulent flow one may also use the following empirical formula:

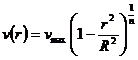(5)

This profile is shown in Figure 5. Close to the wall of the tube the formula 4 and 5 are equivalent.

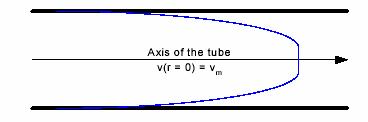
Figure 5. Continuous turbulent profile according to formula 5.

Transient effects

At transitions in the diameter of the tube the flow profile will generally be disturbed over some distance: the flow needs a certain distance to stabilise again.

This effect can also occur due to disturbances such as by a non-smooth wall of the tube or a bend in the tube. The distance over which the disturbances can be observed depends on the velocity of the flow, the diameter of the tube and the initial profile. Empirically the following formula has been established for the distance over which the flow profile can be disturbed.

                                                  (6)

For a laminar flow with in a tube with the radius R = 1 cm one may thus expect a disturbance over a distance of 2 meter. Notice that the formula does not give hard criteria but rather represents an crude estimate [2].

Transition between laminar and turbulent

With increasing Reynolds number it takes more time for small disturbances to die off. Above a certain flow velocity, characterised by the critical Reynolds number , a transition to turbulence will take place: disturbances are longer damped but rather do reinforced one another. Usually one finds 2300<<2600. however, in the case very precisely controlled initial profiles critical Reynolds numbers amounting to more then 10000 have been obtained [2,7].

2.1.b Laser Doppler velocity measurement

Doppler shift

In laser Doppler velocity measurements use is made of the frequency shift that is inflicted on light that is scattered on moving particles. This very small frequency shift remains undetectable under normal circumstances. However, detection can be accomplished by splitting the laser beam and having the two beams cross one another under an angle (figure 6 and 7).

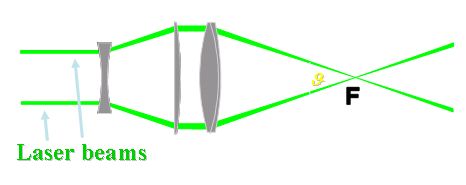
Figure6. A laser is splitted into two equal-intensity, parallel beams. A lens causes these beams to cross and focus at common point (F) [1].

A particle that passes the focal point will scatter light both with a somewhat higher as well as with a somewhat lower frequency. The beam that is directed mainly opposite to the velocity of the particle will give a positive frequency shift (blue shift) and the beam that is directed mainly in conjunctions with the velocity of the particle will give a negative shift (red shift). If a particle passes the focal point of the two beams than both signals will be emitted simultaneously. In fact one has a point source emitting with tow different wavelengths. This situation can be described with a sum-and a difference frequency. The sum frequency can not be detected easily, but the difference frequency can. For the difference frequency, known as the Doppler frequency the following relations holds:

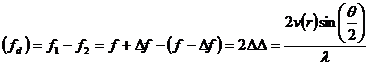           (7)

The observed frequency is thus a measure for the flow velocity. A larger frequency corresponds to a larger flow velocity.[2]

Fringe model

If two coherent laser beams cross one an other an interference pattern ('fringes') will exist in the crossing volume.

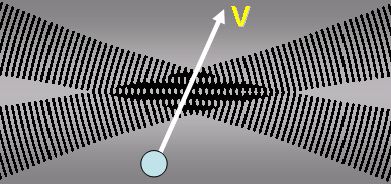
Figure7. LDA description according to the fringe model [1]

The distance between the maxima of the fringes depends on , the crossing angle:

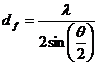                                (8)

The number of maxima is depending on the diameter of the laser beam and the geometry of the set-up. In a properly lined up experimental set-up in the student-lab this number will be approximately be eight. In figure 7 only 4 maxima are depicted for clarity.

A particle that passes the crossing area will scatter the light in the maxima [2].

Light intensity versus time is processed by doppler burst signal processor:

Figure8: Doppler burst before (upper) and after (lower) filtering [1]

This scattered light can be detected by a photo-diode. The frequency of the flashes is a measure for the velocity of the particles perpendicular to the fringes .

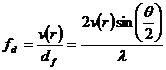                       (9)

Notice that if a particle passes not through the crossing volume but rather through the two separate laser beams two pulses with a lower frequency are observed [2].

Laser optics

A laser power source is required, with excellent frequency stability, narrow line width, small beam diameter, and a Gaussian beam intensity profile (bright at the centre). Typically, HeNe or Argon ion lasers are used, with power levels from 10 miliwatts to 20 watts.

Somewhere close to the laser the beam will be most narrow. This area is called the waist. A positive lens can focus the beam again. Behind the lens a second waist will than result. It may be clear that the smallest and thus best defined crossing volume will be obtained if the two laser beams cross one another in their waists. Furthermore the quality of the lenses used is of importance. To obtain a well defined crossing area carefully grinded lenses should be used that have very little spherical aberration [8].

3 Experimental set-up

The experimental set-up can be divided into three parts:

The fluid circulation part

The optical part

The data acquisition part

3.1.a The fluid circulation

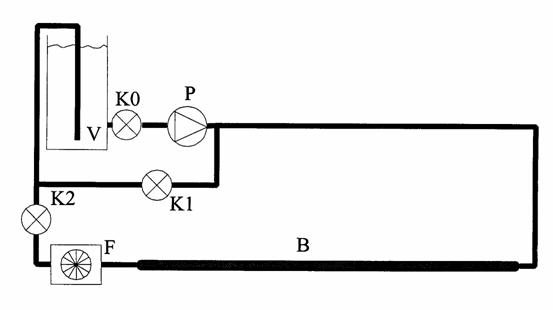
Figure 9. Fluid circulation LDA set-up.

The pump P pumps water from the storage vessel V through the tube B and /or via the bypass with valve K1 back to V. The valve K0 is mounted on the storage vessel and is meant to close off the storage vessel after the experiment. During the experiment K0 is fully opened. The flow velocity through the glass tube B is regulated by the valve K1 that determines the flow through the bypass. The valve K2 is for further fine tuning of the flow in the turning. The frequency of the voltage pulses is to be measured. The flow meter thus measures the total flow through the glass tube. The power supply and the frequency meter are integrated in the case that contains the storage vessel. The calibration curve of the flow meter can be found in the file flow.dat.

For controlling the flow one uses preferably the valve K1 because in that way the load on the pump is minimised, thus leading to a less disturbed flow. The pump pumps water with starch dissolved in it. The starch particles are the light scattering particles. To prevent the grow of algae some chlorine has been added to the water as well [2].

3.1.b Optics

The optical part of the Laser Doppler Velocity measurement is shown in figure 10. The waist of the laser beam is imaged on a grid T with the aid of the lens L1. The grid splits the beam in a number of beams. By lens L2 both of the first order beams are refracted to parallel beams. The 0-th and higher order beams are stopped. Mirror S reflect the beam over 90 degrees for the trivial reason of limiting the space taking up by the experimental set-up as a whole. Lens L3 refracts both of the beams toward one another, thus making them cross in the focal point of L3. In this focal point the glass tube with the starch water or, alternatively, a calibration disc can be placed. The scattered light is detected with a photo diode FD. Both of the firs order beams are stopped by case of the photo diode.

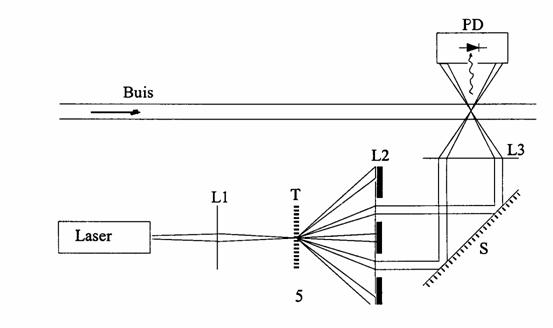
Figure 10. Optics of the LDA set-up.

Following is a sequent step to set up the optic instrument.

Laser beam aligned parallel with the rail from x=0 to infinitive.

Lens L1 with focus = 40 mm placed in 20.5 cm, makes the beam divergent.

The grid placed at 4.5 cm from L1.

Lens L2 with focus = 100 mm placed at x= 33.4 cm makes the beam sharp and parallel again.

The mirror S placed at x = 47.2 cm to reflect two beams at 90 degrees.

Lens L3 to be placed as needed.

3.1.c Data-acquisition

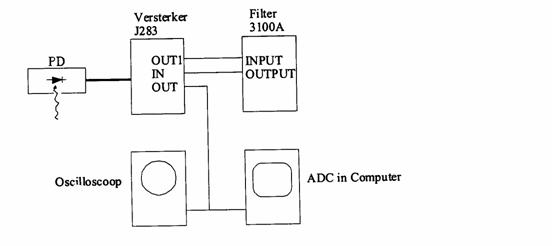
Figure 11: Electronic scheme of the LDA set-up

The signal of the photo diode is amplified by the amplifier J283 (see figure 11). The amplified signal (OUT1) is filtered by the Krone-Hite 3100 filter. The filtered signal is amplified once more by the amplifier J283. This amplifier has a built-in load speaker with separate volume control. This makes it possible to hear the Doppler burst. This feature is useful in the fine-tuning of the apparatus. For the real measurements it is better to turn the sound volume to zero, because in the fact that there is some pick-up between the coil of loudspeaker and the signal. The Krone-Hite 3100 filter is necessary to separate the desired Doppler signal(1-100 Hz) from undesired disturbing signal (sun light, TL - light 50 Hz noise). Moreover the filter takes care that the wave train becomes symmetric with respect to zero (see figure8). This is necessary for further processing by the computer. Adjust the low frequency cut-off of the filter to appr. 1/5 of the Doppler frequency. The high frequency cut-off of the filter should be appr. 5 times the Doppler frequency. The filter can best be used in the RC-mode.

The amplified as well as the filtered signal ( OUT) can be looked at on the oscilloscope. By the use of the digital oscilloscope (HM-205) it is possible to freeze a pulse train, thus allowing careful observation and determination of the frequency.

For each measurements the frequency of the number Doppler bursts should be determinate and averaged. A number of measurements gives the flow profile in the tube.

Determination of the Doppler frequencies 'by hand ' is rather cumbersome and moreover frustrates a full-fletched statistical approach. Therefore this task is taken over by a computer [2].

4.Results and discussions

All graphics and data computation are made by 'TableCurve 2D v5.01' Program.

Calibration

We try to get a nice Doppler signal with the aid of a razor blade. Doppler frequency is calibrated to of rotating Perspex disc. The aim is to get an equation to convert to .

The velocity values that we are found in air also pertain to water. LDV allows a non-invasive measurement is independent of any media.

Table 1: Data-acquisition of Calibration

In Table 1, the velocity was calculated by using the classical formula:

Where R is radius of rotating Perspex disc (mm) and t is time that needs to cycle 1 rotation (sec).

Figure 12.a: Linear regression of versus

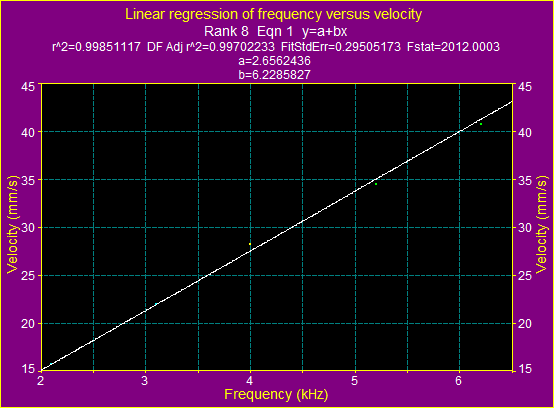
In Figure 11. we fitted measured data with a simple equation:  y=a+bx

This equation shows that the corelation between and v is:

v=2.65+6.22*

Laminar Flow Determination

Laminar flow can be determined by using equation (1) from theory.

Where such information are provided:

g/ml = 997.07 kg/m³

2R=15.16mm=15.16*10^-3m

m²/s

Since viscosity kinematics is known, using equation (2), we have the fallow relation:

Now, we can determinate the Debit:

1.404 l/min

Interpolate Debit- frequency by using table that is given by manual:

Table 2: Debit versus frequency

                   

That means, if you want to get laminar flow the fluid frequency must be set lower than 19.25Hz; and if you want to get turbulent flow, the fluid frequency must be set bigger than 19.25Hz.

Burst frequency measurements for two flows at laminar are recorded in table 3, 4a and 4b.

Table 3. Burst frequency measured with the average velocity:

The next graphs will show fits with the following formulas:

• For laminar flow we used:

R=15.16/2

#F1 = 2*#A*(1-((X-#B)/(R/#C))^2)

Y = IF(#F1>0, #F1,0)

which corresponds to formula (3)

• For turbulent flow we used:

R = 15.16/1.33/2

#F1 = 1-((X-#B)/R)^2

#F2 = IF (#F1>0,#F1,0)

Y = 2*#A*#F2^(1/#C)

which corresponds to formula (4)

Figure 13a. The fitting graphic for using the formula for laminar flow

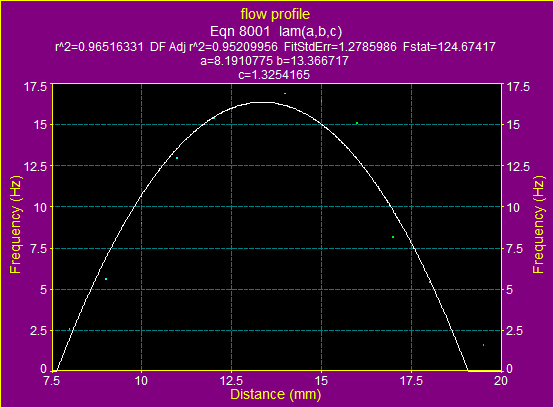
Figure 13b. The fitting graphic for using the formula for turbulent flow

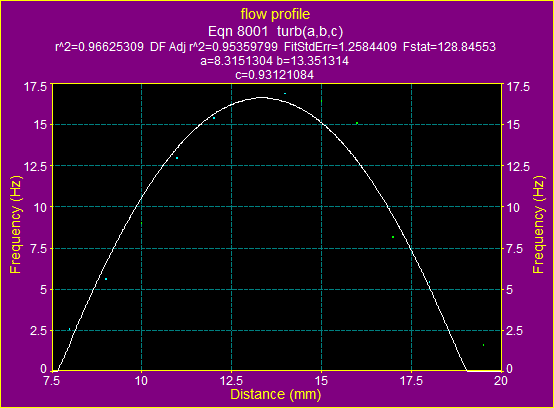
The above two graphs and data show, that for the average velocity the flow is laminar.

Table 4a. Burst frequency measured with the average velocity:

Figure 14a. The fitting graphic for using the formula for laminar flow

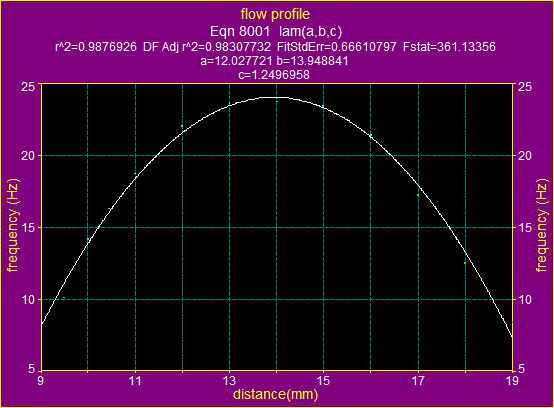
Figure 14b. The fitting graphic for using the formula for turbulent flow

The above two graphs and data show, that for the average velocity the flow is laminar.

Table 4b. Burst frequency measured with the average velocity:

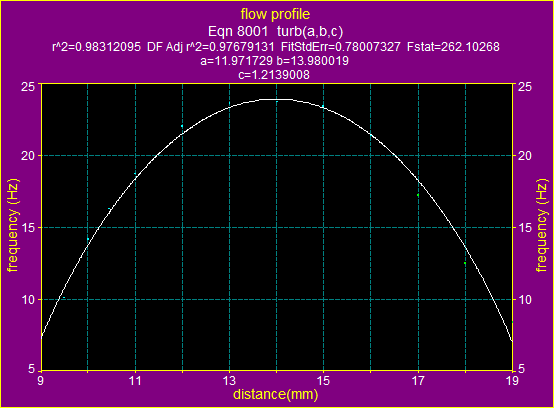
Figure 15a. The fitting graphic for using the formula for laminar flow

Figure 15b. The fitting graphic for using the formula for turbulent flow

The above two graphs and data show, that for the average velocity the flow is laminar.

Table 5.a). Burst frequency measured with the average velocity:

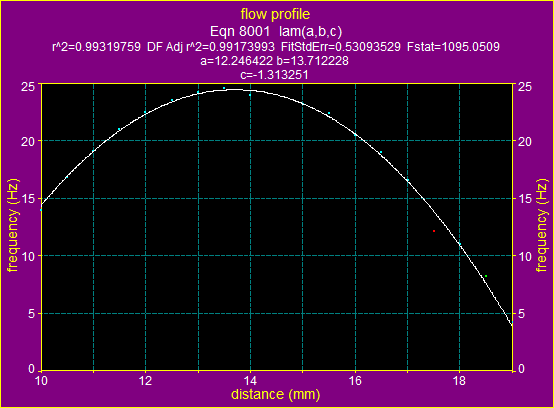
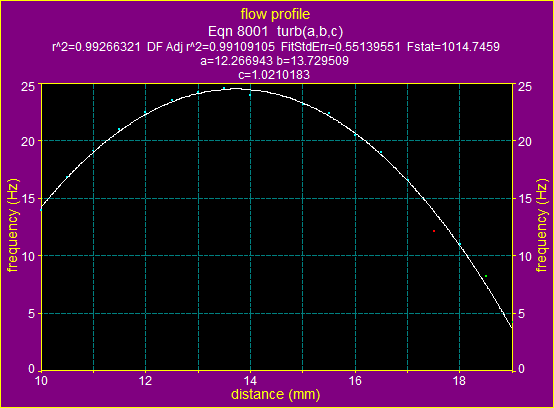
Figure 16.a). The fitting graphic for using the formula for laminar flow

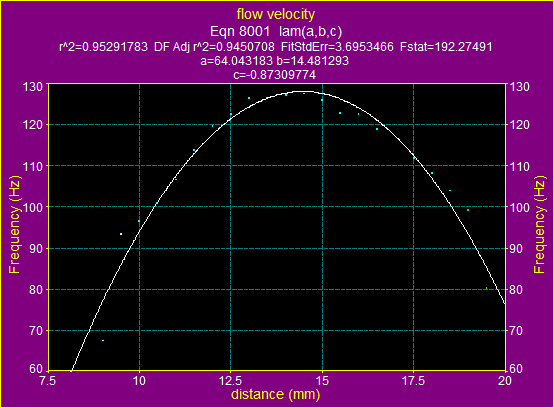
Figure 16.b). The fitting graphic for using the formula for turbulent flow

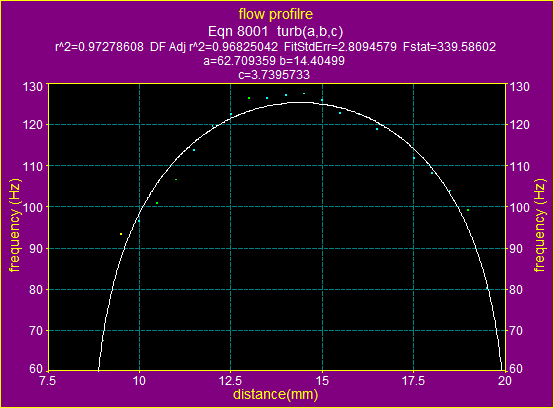
The above two graphs and data show, that for the average velocity the flow is turbulent.

Table 5.b). Burst frequency measured with the average velocity:

Table 5.b). Burst frequency measured with the average velocity:

Figure 17.a). The fitting graphic for using the formula for laminar flow

Figure 17.b). The fitting graphic for using the formula for turbulent flow

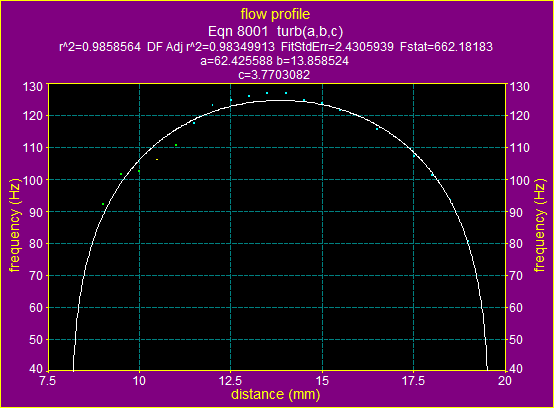
The above two graphs and data show, that for the average velocity the flow is turbulent.

7.Conclusion:

We measured the profile flow for three different velocities: , and.

We found that the flow is laminar for the velocities and ,and turbulent for the velocity .

8.References:

1. https://www.dipmec.unian.it/misure/strumenti/LDA/LDA en html

2. Practicum Module,Laser Doppler Velocity Measurement, Natuurkunde      Rug

3. F.W.Sears, M.W.Zemansky, University Physics, Part 1,(Addison Wesley,1963), blz. 254, [Practicumbibliotheek AN4₁].

4. https://www.coleparmer.com/techinfo/techinfo.asp?htmlfile=V Pdeviations.htm

5. https://hyperphysics.phy-astr.gsu.edu/hbase/pfric.html#vel

6. H.Schlichting, Boundary-Layer Theory 6^th edition, (McGraw-Hill, 1968), Hoofdstuk V en XX.[Bibliotheek Nat./Scheik. 113 A 35]

7. R.S. Brodkey, The Phenomena of Fluid Motions, (Addison-Wesley,1967), Hoofdstuk 9-5, 14-1 en 14-3D. [Bibliotheek Nat./Scheik. 113 A 48].

8. F.A. Jenkins H.E.White,Fundamentals of Optics 4^th edition,( McGraw-Hill, 1981). [Practicumbibliotheek OP6]