DETERMINAREA ACCELERATIEI GRAVITATIONALE LOCALE CU AJUTORUL PENDULULUI MATEMATIC

I.         Introducere teoretica

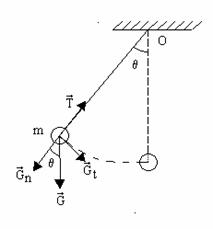
Pendulul matematic este un corp idealizat, format dintr-un punct material de masa m suspendat de un fir usor extensibil, deplasat din pozitia de echilibru cu unghiul q si lasat liber, pendulul va oscila intr-un plan vertical sub actiunea gravitatiei.

Greutatea G se poate descompune dupa doua directii: in lungul firului G_n si tangenta la traiectorie G_t.

Componenta G_n este compensata de tensiunea din fir T, iar componenta G_t este forta cvasielastica care cauta sa aduca pendulul in pozitia de echilibru stabil producand oscilatiile pendulului, fiind singura forta care produce miscarea.

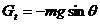     (1)

Conform legii a doua a dinamicii:

    (2)

unde a_t este acceleratia tangentiala iar e este acceleratia unghiulara. Rezulta:

     (3)

      (4)

Introducand notatia: se obtine:

(5)

care reprezinta ecuatia diferentiala a miscarii pendulului matematic.

In cazul oscilatiilor de mica amplitudine unghiulara (0<5^o), se poate face aproximatia sinq q iar ecuatia devine:

        (6)

Aceasta ecuatie, de aceeasi forma cu a unui oscilator armonic, are solutia de forma:

       (7)

unde q_m este amplitudinea unghiulara, w este pulsatia oscilatiilor unghiulare, iar j este faza la momentul initial.

Relatia (7) arata ca elongatia unghiulara este o functie periodica cu perioada:

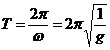     (8)

Cu ajutorul relatiei (8) se poate determina experimental acceleratia gravitationala in locul de observatie:

               (9)

II.       Descrierea aparaturii

Pendulul matematic este format dintr-o bila grea (fier sau plumb) de raza r, fixata la capatul unui fir subtire de otel de lungime l, a carui masa este neglijabila in raport cu masa pendulului (bilei). Celalalt capat al firului este legat de o consola orizontala, fixata in perete.

Pentru masurarea lungimii se foloseste o ruleta, iar perioada pendulului se determina cu un cronometru.

III.     Procedeu experimental

Se masoara lungimea firului l₁ si diametrul sferei d, lungimea pendulului fiind

.

Se repeta masuratorile de mai multe ori si se face media pentru lungimea pendulului l.

Se scoate pendulul din pozitia de echilibru astfel incat amplitudinea unghiulara sa fie 5^o, iar oscilatiile sa fie coplanare intr-un plan vertical.

Se masoara timpul t corespunzator la n=100 oscilatii complete si se determina perioada pendulului .

Se repeta masurarea de mai multe ori si se calculeaza valoarea medie a perioadei.

Se calculeaza acceleratia gravitationala locala cu ajutorul relatiei (9).

Se calculeaza eroarea relativa maxima cu relatia:

        (10)

- unde Dl si DT reprezinta erorile absolute maxime efectuate la masurarea lungimii, respectiv a timpului si care sunt egale cu preciziile instrumentelor folosite.

Se calculeaza eroarea absoluta maxima cu relatia:

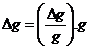              (11)

Se trec datele in tabelul de mai jos care reprezinta rezultatele experimentale.

IV.      Rezultate experimentale

,             .