Schimbarea sistemului de referinta

Conform Principiului mecanic al relativitatii enuntat de Galilei - numit si Principiul relativitatii al lui Galilei, legile si procesele mecanice nu depind de starea de repaus relativ sau de miscare uniforma si rectilinie a sistemului de referinta in care au fost descoperite si experimentate. Viteza, avind valori diferite in sisteme inertiale diferite, reprezinta o exceptie de la acest principiu. De exemplu, un observator care se deplaseaza cu viteza constanta pe o sosea rectilinie sau pe o platforma aflata in miscare uniforma pe sosea, va avea o alta viteza fata de platforma si respectiv fata se sosea. Sa analizam acest exemplu.

Consideram trei puncte materiale O, O' si M (punctele O si O' reprezinta doua repere fixate pe sosea si respectiv pe platforma, iar punctul M reprezinta observatorul) aflate in miscare uniform-rectilinie pe o directie comuna, care au pornit in acelasi moment de timp si din acelasi loc din spatiu, astfel ca in raport cu punctul O considerat in repaus relativ, punctele O' si M se deplaseaza in acelasi sens (cazul in care observatorul se deplaseaza pe sosea), iar in raport cu punctul O' considerat in repaus relativ, punctele O si M se deplaseaza in sensuri opuse (cazul in care observatorul se deplaseaza pe platforma). Aceste doua cazuri sint reprezentate in Fig.1 si respectiv in Fig.2, unde cu S, S' am notat sistemele de referinta cu originile O si respectiv O'.

S S'

| |

| O' |_____________ ______ ____ ______

O|__________ ______ ____ __________ ______ ____ _______●_M

| s₁ = v t ----------- | ----- ----- -------- s₂ = s - v t ----- ----- ---------- |

| -------- ----- ------ ------ s = u t -------- ----- ------ ----- ----- ---- |

s = u t, s₁ = v t, s₂ = s - v t

Fig.1

S S'

| |

| O' |__________ ______ ____ __________________●__M

O |___________ ______ ____ __________ ______ ____ _____

| -- s₁' = v t' -- | ----- ----- ---------------- s' = u t' ----- ----- --------- ----- ------ |

| -------- ----- ------ s₂' = s' + v t' -------- ----- ------ ------ |

s' = u t', s₁' = v t', s₂' = s' + v t'

Fig.2

Cu u si v (u > v) am notat viteza punctului M, respectiv viteza punctelor O, O' unul fata de altul, cu s, s₁ si s₂ am notat distantele parcurse in timpul t de punctele M si O' in raport cu punctul O, respectiv distanta parcursa in timpul t de punctul M in raport cu punctul O', iar cu s', s₁', s₂' am notat distantele parcurse in timpul t' de punctele M si O in raport cu punctul O', respectiv distanta parcursa in timpul t' de punctul M in raport cu punctul O.

Evident t ≠ t', deoarece observatorul nu se poate deplasa in acelasi timp si cu aceeasi viteza in sisteme inertiale diferite - atit pe sosea cit si pe platforma. Totodata, se constata ca distanta parcursa intr-un sistem de referinta poate fi cel mult proportionala cu distanta parcursa in raport cu sistemul de referinta respectiv. De exemplu, comparind distantele s si s' parcurse de observator pe sosea si respectiv pe platforma cu distantele s'₂ si respectiv s₂ parcurse de observator fata de sosea si respectiv fata de platforma, constatam ca acestea pot fi cel mul proportionale, asadar rezulta relatiile

s = k (s' + v t'), s' = k (s - v t) (*)

unde k este un factor de proportionalitate neunitar ce va fi determinat.

Desigur ca oricare ar fi locul si momentul in care se afla, presupunind ca se deplaseaza pe sosea, observatorul se poate intreba care ar fi locul si momentul in care s-ar afla in cazul in care ar dori sa-si continue deplasarea pe platforma, sau care ar fi fost locul si momentul in care s-ar fi aflat in ipoteza ca s-ar fi deplasat chiar de la inceput pe platforma, sau, in sfirsit, care este locul si momentul in care se afla in ipoteza ca tocmai a trecut de pe sosea pe platforma. In ce priveste locul in care s-ar afla, s-ar fi aflat sau se afla in cazurile anterior mentionate, raspunsul este cunoscut daca poate fi calculata distanta s' exprimata in cea de a doua relatie din (*).

Presupunind ca observatorul se deplaseaza pe sosea, vom spune despre aceasta deplasare ca este reala, iar despre deplasarea posibila (dar care nu s-a produs in fapt) a observatorului pe platforma ca este virtuala. In acest caz, timpul t si distantele reprezentate in Fig.1 sint reale, iar timpul t' si distantele reprezentate in Fig.2 sint virtuale. Ca urmare, cea de a doua relatie din (*) exprima distanta virtuala parcursa de observator pe platforma in functie de distanta reala parcursa de observator fata de platforma. In eventualitatea schimbarii sistemului de referinta, deci daca observatorul trece de pe sosea pe platforma, atunci deplasarea observatorului pe platforma devine reala, iar deplasarea observatorului pe sosea devine virtuala. In acest caz, prima relatie din (*) exprima distanta virtuala parcursa observator pe sosea in functie de distanta reala parcursa de observator fata de sosea.

Pentru a determina factorul k, in prealabil este necesar sa punem in evidenta existenta relatiilor

t = k (t' + s'), t' = k (t - s) (**)

care pot fi deduse in acelasi mod in care au fost deduse si relatiile (*), insa de data aceasta fixind locul din spatiu in care se gasesc puncrele O, O', M si exprimind in timp intervalul dintre ele.

Pornim de la relatiile

s = u t (1₁)

s₁ = v t (2₁)

s₂ = s - v t (3₁)

care descriu miscarea in spatiu in timpul t a punctelor O, O', M reprezentata in Fig.1. Aceste relatii au fost obtinute pe baza ipotezei ca miscarea este relativa in spatiu si absoluta in timp. Cu alte cuvinte, am presupus ca numarul unitatilor de masura parcurse in spatiu este relativ si ca numarul unitatilor de masura parcurse in timp este absolut. Notind cu m unitatea de masura pentru spatiu si cu h₀ distanta parcursa de punctul M in raport cu punctul O in unitatea de timp,

h₀ = u m (α₀)

distanta dintre punctele O si M in momentul t se poate reprezenta sub forma

OM = s m = t h₀ (β₀)

Sau, notind cu h₁ distanta parcursa de punctul O' in raport cu punctul O in unitatea de timp,

h₁ = v m (α₁)

distanta dintre punctele O si O' in momentul t se poate reprezenta sub forma

OO' = s₁ m = t h₁ (β₁)

Relatiille (α₁), (β₁) pot fi obtinute din relatiile (α₀), (β₀) presupunind ca OO' = a OM si notind h₁ = a h₀, v = a u, s₁ = a s, unde a este este un factor pozitiv subunitar (0 < a < 1).

Se observa ca din (α₀) si (β₀) rezulta (1₁), iar din (α₁) si (β₁) rezulta (2₁). Egalitatea (3₁) se obtine tinind cont ca O'M = OM - OO', asdar scazind (2₁) din (1₁) si notind s₂ = s - s₁.

In mod similar, pornind de la ipoteza ca miscarea este relativa in timp si absoluta in spatiu, rezulta relatiile

t = s (1₂)

t₁ = s (2₂)

t₂ = t - s (3₂)

care descriu miscarea in timp pe distanta s a punctelor O, O', M. In acest caz am presupus ca numarul unitatilor de masura parcurse in timp este relativ si ca numarul unitatilor de masura parcurse in spatiu este absolut. Notind cu h unitatea de masura pentru timp si cu m₀ intervalul de timp parcurs de punctul M in raport cu punctul O pe unitatea de spatiu,

m₀ = h (γ₀)

intervalul de timp dintre punctele O si M in locul s se poate reprezenta sub forma

OM = t h = s m₀ (δ₀)

Tinind cont de (γ₀), din (δ₀) rezulta (1₂).

Pe de alta parte, daca amplificam relatiille (γ₀) si (δ₀) cu factorul a si avem in vedere notatiile m₁ = a m₀, v = a u, t₁ = a t, rezulta relatiile

m₁ = h (γ₁)

si respectiv

OO' = t₁ h = s m₁ (δ₁)

pe baza carora rezulta relatia (2₂). In sfirsit, notind t₂ = t - t₁, din (1₂) si (2₂) rezulta (3₂).

Intervalele de timp de marime h si h parcurse de punctele M si respectiv O' in raport cu punctul O (calculate in ipoteza ca miscarea este relativa in timp si absoluta in spatiu) corespund distantelor de marime m si m parcurse de punctele M si respectiv O' in raport cu punctul O (calculate in ipoteza ca miscarea este relativa in spatiu si absoluta in timp).

Reunite, relatiile (1₁), (2₁), (3₁) si (1₂), (2₂), (3₂) se scriu

s = u t, t = s (1)

s₁ = v t, t₁ = s (2)

s₂ = s - v t, t₂ = t - s (3)

Cum se constata, relatiile (1), (2), (3) pot fi obtinute daca pornim de la ipoteza ca miscarea in spatiu si timp este atit absoluta cit si relativa. In cazul miscarii absolute, intervalul spatiu-timp parcurs este absolut, iar in cazul miscarii relative, intervalul spatiu-timp parcurs este relativ. In primul caz, miscarea in spatiu si timp a punctelor O, O' M este definita de modificarea locului-moment in care se afla, iar in cazul al doilea, miscarea in spatiu si timp a punctelor O, O' M este definita de modificarea intervalului spatiu-timp dintre ele. Modul cum se modifica distantele relative dintre punctele O, O', M, in cazul in care se modifica momentul absolut in care se afla, este descris de relatiile (1₁), (2₁), (3₁), iar modul cum se modifica intervalele de timp relative dintre punctele O, O', M, in cazul in care se modifica locul absolut in care se afla, este descris de relatiile (1₂), (2₂), (3₂).

Pornind de la miscarea in spatiu in timpul t' descrisa in Fig.2 si avind in vedere ipoteza mai sus mentionata, se obtin relatiile

s' = u t', t' = s' (1')

s'₁ = v t', t'₁ = s' (2')

s'₂ = s' + v t', t'₂ = t' + s' (3')

In acest caz, in locul-moment absolut (s', t'), intre punctele O' si M exista intervalul spatiu-timp relativ (s', t') dat de (1'), intre punctele O si O' exista intervalul spatiu-timp relativ (s'₁, t'₁) exprimat in (2'), iar conform (3'), intre punctele O si M exista intervalul spatiu-timp relativ (s'₂, t'₂).

In continuare, comparind intervalul spatiu-timp real cu intervalul spatiu-timp virtual dintre punctele O si M, presupunind ca acestea sint (s, t) dat de relatiile (3) si respectiv (s'₂, t'₂) dat de relatiile (3'), rezulta sistemul de ecuatii cu doua necunoscute

s = k (s' + v t'), t = k (t' + s') (4)

care, rezolvat in raport cu s', t', conduce la solutiile

s' = k (s - v t), t' = k (t - s) (4')

unde factorul k are valoarea

k = 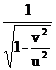(5)

Se observa ca relatiile (4) si (4') sint de fapt (*) si (**).

Relatiile (4) si (4') definesc trecerea dintr-un sistem de referinta inertial intr-un alt sistem de referinta inertial. Cum se constata, intervalul spatiu-timp virtual parcurs intr-un sistem de referinta, de exemplu intervalul spatiu-timp (s', t') parcurs de punctul M in raport cu punctul O' in sistemul de referinta S', nu se identifica cu intervalul spatiu-timp real parcurs in raport cu sistemul de referinta respectiv, asadar cu intervalul spatiu-timp (s₂, t₂) parcurs de punctul M in raport cu punctul O' in sistemul de referinta S. Pe de alta parte, cunoscind intervalul spatiu-timp real parcurs in raport cu un sistem de referinta, putem determina intervalul spatiul-timp virtual parcurs in sistemul de referinta respectiv. Aceste concluzii rezulta din relatiile (4'), in ipoteza ca miscarea punctului M in sistemul de referinta S este reala. In cazul schimbarii sistemului de referinta, intervalul spatiu-timp virtual devine real, iar intervalul spatiu-timp real devine virtual. De exemplu, daca presupunem ca incepind din locul-moment (s, t) in sistemul de referinta S, respectiv (s', t') in sistemul de referinta S', punctul M isi continua deplasarea reala in sistemul de referinta S', atunci intervalul spatiu-timp (s', t') devine real, iar intervalul spatiu-timp (s, t) devine virtual. In acest caz, pentru a determina intervalul spatiu-timp virtual (s, t) parcurs de punctul M in raport cu punctul O in sistemul de referinta S, in functie de intervalul spatiu-timp real (s'₂, t'₂) parcurs de punctul M in raport cu punctul O in sistemul de referinta S', utilizam relatiile (4).

Cele mai sus prezentate conduc la concluzia ca nu viteza reprezinta o exceptie de la Principiul mecanic al relativitatii, asa cum afirmam la inceput, ci spatiul si timpul. Intr-adevar, este exclusa posibilitatea deplasarii cu aceeasi viteza 'in raport' cu sisteme inertiale diferite, dar asta nu inseamna ca este exclusa posibilitatea deplasarii cu aceeasi viteza 'in' sisteme inertiale diferite. Evident, aceasta concluzie este valabila in ipoteza ca schimbarea sistemului de referinta este definita de relatiile (4) si (4'), nu de relatiile (3) si (3') (transformarile Galilei).