Siruri

Chestiuni elementare

despre siruri

Prezenta lucrare isi propune prezentarea unor aspecte elementare privind sirurile de numere reale.

In mod obisnuit, prin sir se intelege o infinitate de numere, distincte sau, nu, scrise unul dupa altul. Exemplu, sirul numerelor naturale:

Definitie. Numim sir orice functie f : N R, f(n) = a_n.

Notam (a_n)_n

Exemple de siruri:

2, ., n, n, .

3) 10, 10², 10³, 10⁴, ., 10ⁿ, .

4) 1, , , , ., , .

, , , ., , .

Definitie. Sirul (a_n)_n este marginit daca exista M > 0 astfel incat a_n M, pentru orice nIN

Exemplu: sirul a_n = cos nΠ este marginit, deoarece termenii sai sunt mai mari sau egali cu -1 si mai mici sau egali cu 1.

Definitie. Sirul (a_n)_n este monoton crescator daca a_n a_n+1. Sirul (a_n)_n este monoton descrescator daca a_n a_n+1.

Exemple: sirul "0, 1, 2, 3,., n,." este crescator; sirul "1, , , , ., , ." este descrescator.

Notiunea de convergenta

Daca observam ca termenii sirului (a_n)_n se apropie din ce in ce mai mult de numarul a (se "ingramadesc"), pe masura ce n creste, vom avea o viziune intuitiva asupra convergentei sirului. Vom spune ca a_n a (a_n tinde, converge catre a), a fiind limita sirului. Vom nota .

Mai exact:

Definitie. Sirul (a_n)_n este convergent catre a sau are limita a daca orice vecinatate a lui a (interval deschis care-l contine pe a) contine toti termenii sirului, exceptand (eventual) un numar finit de termeni.

Sau:

Definitie. Sirul (a_n)_n este convergent catre a (are limita a) daca e > n_e > (un rang depinzand de e), astfel incat n n_e, sa avem a_n a < e

Observatie. Limita unui sir, daca exista, este unica.

Teorema. Orice sir monoton si marginit este convergent.

Exemplu. Sirul a_n = se constata usor ca este descrescator: 1 > > > > > . si marginit inferior de 1; deci = 1.

Proprietati ale sirurilor convergente:

limita modulului este egala cu modulul limitei;

limita sumei (diferentei, produsului, catului - daca exista) este egala cu suma (diferenta, produsul, catul) limitelor;

constanta iese in fata limitei;

limita radicalului este egala cu radicalul limitei;

limita unei puteri se distribuie bazei si exponentului, adica lim(x^y) = (limx)^limy;

limita logaritmului este egala cu logaritmul limitei; etc.

Operatii cu

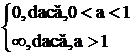); a ; la inmultirea (impartirea) infinitilor se aplica regula semnelor; = 0; = ; a = ; ^a = 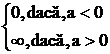; 0 ; log_a0 = ; log_a

Operatii fara sens: ; ; ; 1

Aspectele prezentate mai sus, aprofundate pe baza de exemple, vor constitui baza calculului limitelor de siruri.