Derivata intai
IV.1 Calculam derivata si stabilim domeniul de derivabilitate. In general, domeniul maxim de definitie , domeniul de derivabilitate cu exceptia:
IV.1.1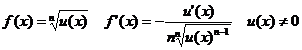 
!!!
IV.1.2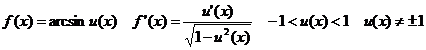
!!!
IV.1.3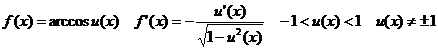 
!!!
IV.2 Semitangente la grafic
IV.2.1
domeniului de
derivabilitate => 
si este finita
y-f(x0)=f'(x0)(x-x0) tangenta la Gf in punctul M0(x0,f(x0))
caz particular f'(x0)= 0 => tangenta la Gf in punctul M0(x0,f(x0)) este orizontala
IV.2.2
tangenta la Gf este
verticala
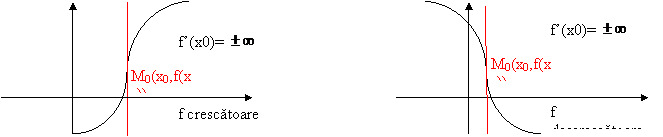
IV.2.3 
si cel putin
una este finita =>
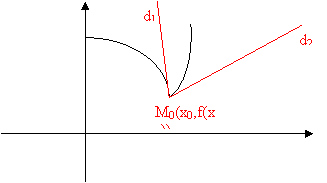
Gf are semitangenta la stanga d1: y-f(x0)=f's(x0)(x-x0) si
Gf are semitangenta la dreapta d2: y-f(x0)=f'd(x0)(x-x0).
M0(x0,f(x0)) punct unghiular.
IV.2.4 
ambele infinite =>
M0(x0,f(x0)) punct de
intoarcere.
IV.3 Punctele critice
f'(x)=0
IV.4 Intervalele in care derivata are semn constant
a) 
strict crescatoare pe I
b) 
strict descrescatoare pe I
IV.5 Puncte de extrem
M(x0,f(x0)) punct de maxim/minim
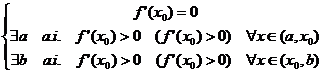
V. Studiul derivatei a doua
V.1 Se calculeaza derivata a doua
V.2 Se determina semnul derivatei a doua
+ convexa
concava
V.3 Punctele de inflexiune x0
f''(x0)=0
semne contrare la stanga si la dreapta lui x0
