ECUATIA DE GRADUL AL II-LEA
Fie problema:
O casa are baza in forma de dreptunghi, cu lungimea de 13m si latimea de 7,5m. Proprietarul doreste sa-si construiasca o bordura de ciment, de aceeasi latime pe toate laturile casei (vezi desenul). Fondurile pe care le are il obliga la o suprafata construibila de 33m2.
![]() x 13m
x 13m
In conditiile date, care este latimea
maxima pe care o poate avea bordura
casei?
|
|
|
|
|
|
|
|
|
|
|
CASA |
|
|
|
|
|
|
|
![]() 7,5m
7,5m
Pentru rezolvarea acestei probleme notam cu x, in metri, latimea bordurii si putem scrie urmatoarea ecuatie:
4x2 + 41x =33 4x2 + 41x -33 = 0
Se observa ca aceasta ecuatie este diferita de tipul de ecuatii invatate anterior. Deoarece necunoscuta x apare si la puterea a doua, aceasta ecuatie spunem ca se numeste de gradul al II-lea.
Forma generala a unei ecuatii de gradul al II-lea este:
ax2 + bx + c = 0 (1)
unde a,b,c sunt numere reale, cu a 0. Aceasta ecuatie se numeste de gradul al II-lea cu coeficienti reali.
Rezolvarea ecuatiei (1) presupune determinarea tuturor solutiilor (radacinilor) sale.
Existenta radacinilor reale precum si numarul lor depind de expresia
b2 - 4ac (2)
care se numeste discriminantul ecuatiei de gr. al II-lea si se noteaza cu D
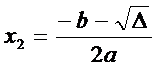
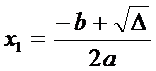 Daca
discriminantul este pozitiv, atunci ecuatia are doua
radacini reale, diferite intre ele:
Daca
discriminantul este pozitiv, atunci ecuatia are doua
radacini reale, diferite intre ele:
(3)
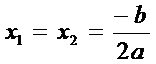 In cazul in care D = 0, atunci ecuatia are doua solutii reale,
egale:
In cazul in care D = 0, atunci ecuatia are doua solutii reale,
egale:
Putem avea si doua cazuri particulare de rezolvare a ecuatiei (1) si anume:
a)Daca coeficientul b al lui x este nul atunci ecuatia devine:
ax2 + c = 0
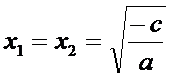 In aceasta
situatie ecuatia are doua solutii reale, egale numai
daca c si ele sunt:
In aceasta
situatie ecuatia are doua solutii reale, egale numai
daca c si ele sunt:
b)Daca termenul liber c este egal cu zero. atunci forma ecuatiei este:
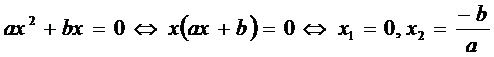 ax2 + bx = 0
ax2 + bx = 0
Rezolvarea este:
Ecuatia de gradul al doilea, care are discriminantul D 0, admite si doua forme particulare importante, si anume:
![]() 1. Daca in ecuatia
(1) coeficientul b al lui x este de forma: b = 2b1
atunci obtinem: ax2 + 2b1x + c = 0, pentru care discriminantul devine
1. Daca in ecuatia
(1) coeficientul b al lui x este de forma: b = 2b1
atunci obtinem: ax2 + 2b1x + c = 0, pentru care discriminantul devine
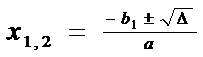
![]()
iar radacinile vor fi de forma
.
2. Forma redusa a ecuatiei de gradul al doilea. O ecuatie de gradul al doilea se numeste redusa daca coeficientul lui x2 = 1. Forma generala a ecuatiei reduse este: x2 + px + q = 0,
unde p, q sunt numere reale.
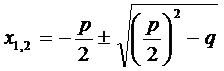 Daca in relatiile (1), (2), (3) inlocuim a, b, c
respectiv cu 1, p, q vom obtine formula pentru radacinile
ecuatiei de gradul al doilea sub forma redusa:
Daca in relatiile (1), (2), (3) inlocuim a, b, c
respectiv cu 1, p, q vom obtine formula pentru radacinile
ecuatiei de gradul al doilea sub forma redusa:
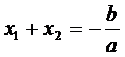
![]() Intre coeficientii
si radacinile unei ecuatii de gr. al II-lea (1) se poate
stabili
Intre coeficientii
si radacinile unei ecuatii de gr. al II-lea (1) se poate
stabili ![]()
un set de relatii cu aplicatie practica:
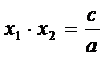
![]()
(4)
Relatiile (4) poarta denumirea de Relatiile lui Viète. Cu aceste relatii se poate deci calcula suma si produsul radacinilor reale ale ecuatiei (1) fara a le afla efectiv.
s = x1 + x2 , p = x1 x2
Aceste relatii ne permit sa formam o ecuatie de gr. al II-lea atunci cand cunoastem radacinile, astfel:
x2 - sx + p = 0
De utilitate practica mai este si studiul semnelor radacinilor unei ecuatii de gr al II-lea, mai ales cand aceasta este cu parametru. Acest lucru se poate face studiind semnul discriminantului, sumei si produsului radacinilor din relatia (2), respectiv din relatiile lui Viète (4).
Se poate construi urmatorul tabel:
|
D<0 |
Ecuatia (1) nu are radacini reale. |
|
|
D |
p>0 |
s>0 x1>0, x2>0 |
|
s<0 x1<0, x2<0 |
||
|
p<0 |
s>0 x1>0, x2<0, x1 > x2 |
|
|
s<0 x1>0, x2<0, x1 < x2 |
||
Observatii: 1. Fie s . Ecuatia are radacini reale numai daca p 0. In acest caz avem x1 +x2 = 0 adica x1 = -x2 .
2. Fie p = 0 . Atunci x1 = 0 si x2 = s.
Sa rezolvam ecuatia problemei din introducerea lucrarii:
4x2 + 41x - 33 = 0
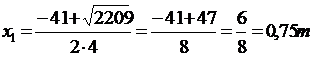 D
D
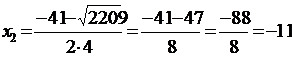
aceasta solutie nu este acceptabila din
punctul de vedere al problemei pentru ca este negativa. Deci bordura casei va avea latimea maxima de 0,75m.
2. Sa se studieze natura radacinilor ecuatiei
mx2 +(m - 1)x - (m - 2) = 0 in functie de parametrul real m.
Vom calcula si vom studia, mai intai, semnul pentru D, s, si p.
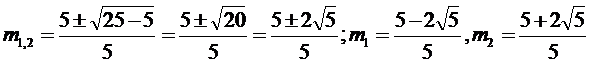 D= (m -1)2
+ 4m(m -2)= m2 - 2m +1 +4m2 - 8m = 5m2 - 10m
+1
D= (m -1)2
+ 4m(m -2)= m2 - 2m +1 +4m2 - 8m = 5m2 - 10m
+1
D va fi negativ intre valorile m1 si m2 si pozitiv in rest.
|
|
- 0 1 + |
|
1 - m |
- - - - - - - - |
|
m |
0 + + + + + + + + + + + + + |
|
s |
/ + + + + + + 0 - - - - - - - - - |
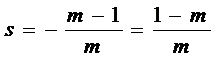
|
|
- 0 2 + |
|
2 - m |
|
|
m |
0 + + + + + + + + + + + + + |
|
p |
0 - - - - - - - - - |
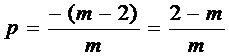
![]()
|
m |
D |
s |
p |
natura radacinilor |
|
|
|
|
|
x1 x2IR, x1<0, x2> x1 > x2 |
|
|
|
|
|
Ec de gr I , x - 2 = 0, x = 2 |
|
|
|
|
|
x1 x2IR, x1>0, x2> |
|
|
|
|
|
x1=x2IR+ |
|
|
|
|
|
Ecuatia data nu are solutii reale. |
|
|
|
|
|
Ecuatia data nu are solutii reale. |
|
|
|
|
|
Ecuatia data nu are solutii reale. |
|
|
|
|
|
x1=x2IR-- |
|
|
|
|
|
x1 x2IR-- |
|
|
|
|
|
x1 x2IR, x1=0, x2< |
|
|
|
|
|
x1 x2IR, x1<0, x2> x1 > x2 |