Ecuatia de gradul II, Sisteme de inecuatii si ecuatii, functia de gradul II

4. FUNCTIA DE GRADUL  II

f: |R®|R, f(x)=ax²+bx+c    a, b, cI|R, a¹0.

Forma canonica: f(x)=a(x+ )² .

Monotonie:

Semn:

Ø     daca D<0    ;

Ø     daca D=0     ;

Ø     daca D>0 ;

Ø     daca a>0 ;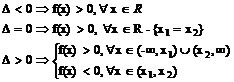

Ø     daca a<0 .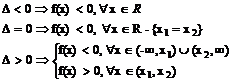

Intersectia cu axele:

Ø     GfÇOX=;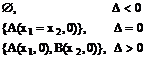

Ø     GfÇOY=.

Varful parabolei: 

Ø     V(,);

Ø     daca a>0 -"È"TV_min - varf minim;

Ø     daca a<0 -"Ç"TV_max - varf maxim. 

Grafic:

Ø     graficul functiei de gradul II este o parabola;

Ø 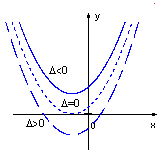    daca c=0 parabola trece prin originea axelor;

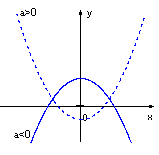
Ecuatia de gradul II:

Ø     ax²+bx+c=0   a, b, cI|R, a¹0;

Ø     D=b²-4ac - discriminantul (delta);

Ø     daca ;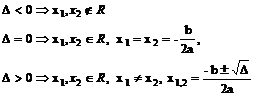

Ø     relatiile lui Francois Viète sau relatii intre radacini si coeficienti (D³0): ;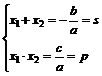

Ø     formarea ecuatiei de gradul al doilea cand se cunosc radacinile: x² - sx + p = 0;

Ø     descompunerea trinomului de gradul II in produs de polinoame de gradul intai: ax²+bx+c=a(x-x₁)(x-x₂);

Ø     daca b=2b₁⇒ ax²+2b₁x+c=0 ⇒D₁=b₁²-ac>0, x₁,x₂=- formula pe jumatate;

Ø     daca ax²+bx+c=0 |:a¹0 ⇒ x²+x+=0, =p, =q ⇒ x²+px+q=0 - forma redusa;

Ø     discutia naturii si semnului radacinilor in functie de semnele lui D, s si p:

Inecuatia de gradul II:

Ø     ax²+bx+c<0   a, b, cI|R, a¹0;

Ø     ax²+bx+c£0   a, b, cI|R, a¹0;

Ø     ax²+bx+c>0   a, b, cI|R, a¹0;

Ø     ax²+bx+c³0   a, b, cI|R, a¹0;

Ø     se rezolva ecuatia de gradul II atasata, se studiaza semnul pe |R utilizand semnul functiei de gradul II;

Ø     solutia inecuatiei este acel interval sau reuniune de intervale care satisface cerintele (<, >, £, ³).

Sisteme de inecuatii de gradul II:

Ø     sunt sisteme formate din doua sau mai multe inecuatii de gradul II;

Ø     solutia sistemului este intersectia tuturor solutiilor inecuatiilor din sistem.

Semnul unor expresii:

Ø     E(x)=,  a₁,a₂,b₁,b_2,,c₁,c₂I|R,  a₁,a₂¹0, ;

Ø     se studiaza semnele functiilor , intr-un tabel;

Ø     se tine cont de faptul ca o fractie este pozitiva Û numaratorul si numitorul au acelasi semn;

Ø     se tine cont de faptul ca o fractie este negativa Û numaratorul si numitorul au semne contrare;

Ø     tinand cont de semnele celor doua functii se determina semnul expresiei pe |R.

Inecuatii cu modul:

Ø     |ax²+bx+c|<m    a, b, c, mI|R, a¹0;Û -m<ax²+bx+c<mÛ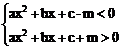T se rezolva ca si sistemele de inecuatii.

Sisteme de ecuatii:

Ø     formate dintr-o ecuatie de gradul I si una de gradul II cu 2 necunoscute: , se rezolva prin metoda substitutiei;

Ø     sisteme omogene: 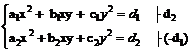se aduna ecuatiile T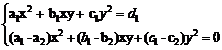ecuatia a doua se imparte cu x² (respectiv y²), dupa care se face substitutia  (respectiv ) obtinandu-se o ecuatie de gradul II T 1 sau 2 sisteme formate dintr-o ecuatie de grad I si una de grad II;

Ø     sisteme simetrice: se noteaza , se utilizeaza identitatile: .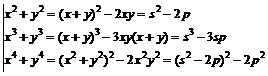

Ø    

Ø