Locuri geometrice

Def.: Locul geometric este multimea de puncte care au aceeasi proprietate.

Mediatoarea unui segment este dreapta perpendiculara pe segment dusa prin mijlocul segmentului. Existenta si unicitatea mediatoarea rezulta din faptul ca mijlocul unui segment exista si este unic, perpendiculara printr-un punct al dreptei pe dreapta exista si este unica.

Teorema 1: Orice punct de pe mediatoarea unui segment este egal departat de capetele segmentului.

Dem.: Se considera (AB), , si M un punct de pe mediatoarea segmentului (AB) (Fig.1.1). Daca , afirmatia este evidenta. Daca , (C.C.) si rezulta , deci .

	Fig. 1.1

Teorema 2: Orice punct egal departat de capetele unui segment apartine mediatoarei segmentului.

Fig. 1.2

Dem.: Se considera (AB) si M un punct astfel incat (Fig.1.2). Daca , atunci M este mijlocul segmentului (AB) si apartine mediatoarei. Daca , fie O mijlocul segmentului (AB). (LLL). Deci . Deoarece cele doua unghiuri sunt si suplementare, rezulta ca , ceea ce inseamna ca MO este mediatoarea segmentului (AB).

Asadar mediatoarea unui segment este locul geometric al punctelor egal departate de capetele segmentului.

Un alt exemplu de loc geometric este bisectoarea unui unghi.

Bisectoarea unui unghi este dreapta care trece prin intersectia a doua drepte diferite, impartind unghiul format de cele doua drepte in doua unghiuri congruente.

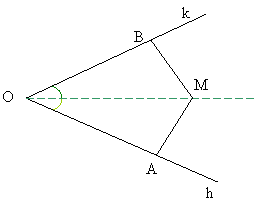
Teorema 3: Bisectoarea unui unghi este locul geometric al punctelor din interiorul unghiului egal departate de laturile unghiului, reunit cu varful unghiului.

Fig. 1.3

Dem.: a) Se va arata ca orice punct de pe bisectoare este egal departat de laturile unghiului (Fig.1.3). Fie , O varful unghiului, s bisectoarea lui si . Se noteaza cu A si B picioarele perpendicularelor din M pe h si respectiv k. (IU) .

b) Se va arata ca orice punct M egal departat de laturile unghiului si se afla in interiorul unghiului, apartine bisectoarei. Se noteaza cu A si B picioarele perpendicularelor duse din M pe laturile unghiului. , (OM) latura comuna si

(IC) OM bisectoare.

Pe baza proprietatilor de loc geometric ale bisectoarelor si mediatoarelor se pot demonstra urmatoarele doua teoreme referitoare la concurenta bisectoarelor si mediatoarelor unui triunghi.

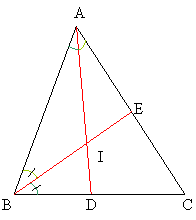
Teorema 4 Bisectoarele unghiurilor unui triunghi sunt concurente.

Dem.: Din teorema transversalei rezulta ca bisectoarele unghiurilor A si B intersecteaza pe (BC) si (AC) in cate un punct D, respectiv E (Fig.1.4). Din aceeasi teorema rezulta ca exista puntul I, . Asadar . Din proprietatea punctelor bisectoarei unui unghi rezulta d(I,BC) = d(I,AB), d(I,AB) = d(I,AC) si deci d(I,BC) = d(I,AC) si pentru ca rezulta ca [CI este bisectoarea unghiului C.

	Fig. 1.4

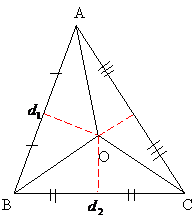
Teorema 5 Mediatoarele laturilor unui triunghi sunt concurente.

Dem.: Fie un triunghi ABC, mediatoarele segmentelor (AB) respectiv (BC), (Fig.1.5). Din proprietatea punctelor mediatoarei , deci O apartine mediatoarei segmentului (AC).

	Fig. 1.5

Rezolvarea unor probleme de loc geometric

Pe langa bisectoarea, mediatoarea, cercul sau arcul, luate ca locuri geometrice, se mai pot adauga si:

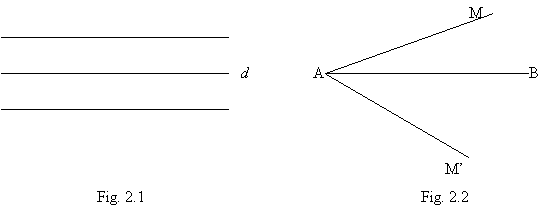
multimea punctelor situate la aceeasi distanta de o dreapta data d este reuniunea a doua drepte paralele cu d, situate in semiplane diferite (Fig.2.1.);

fiind data o semidreapta (AB, multimea punctelor M pentru care unghiul are o masura data este reuniunea a doua semidrepte deschise, cu originea comuna in A, situate in semiplane diferite fata de AB (Fig.2.2.).

Rezolvarea acestor probleme se realizeaza in doua etape: prima este aceea in care se incearca determinarea intuitiva a multimii respective, iar in etapa urmatoare se demonstreaza efectiv ca aceasta multime este locul geometric cautat.

Problemele au urmatorul tip: pozitia unui punct M se determina dupa o regula data in functie de pozitia altor puncte si se cere sa se afle locul geometric al punctelor M atunci cand unul sau mai multe din celelalte puncte sunt variabile si parcurg multimi date

In prima etapa se incearca gasirea unor puncte speciale ale locului geometric.

Determinarea a trei puncte ale locului geometric poate sugera daca este vorba despre un segment de dreapta sau un arc de cerc, dupa care se incearca a se demonstra presupunerea facuta. Astfel, daca se presupune ca punctul M descrie o dreapta, se va demonstra, de exemplu, ca M este la o distanta constanta de o dreapta data sau ca AM formeaza unghi constant cu o semidreapta fixa. Daca se presupune ca este vorba despre un arc de cerc se va arata, de exemplu, ca punctele sunt la distanta constanta de un punct fix sau determina un unghi de masura constanta cu doua puncte fixe si este situat intr-unul din cele doua semiplane determinate de punctele fixe.

Dupa ce s-a aratat in acest fel ca punctele locului geometric apartin unei multimi M (o dreapta, un cerc, un arc de cerc, etc) se continua astfel:

se arata ca, reciproc, orice punct al multimii M apartine locului geometric (in care caz locul geometric este M), sau ca acest lucru nu este adevarat.

se determina submultimea a lui M care apartine locului geometric; atunci locul geometric cautat este .

Exemple:

Se da triunghiul ABC, dreptunghic in A. Proiectam in P, Q punctele B si C pe o dreapta variabila d, care trece prin A. Sa se afle locul geometric descris de mijlocul M al segmentului [PQ], cand dreapta d se roteste in jurul lui A.

Rezolvare:

Fie A', B', C' mijloacele lui . Daca d ia pozitia AB, atunci P = B si Q = A, deci C' apartine locului geometric, la fel B'. Se observa usor ca daca d ajunge in pozitia AA', punctul M este in A'. Deci A', B', C' apartin locului geometric, ceea ce ne conduce la presupunerea ca locul cautat este cercul P circumscris dreptunghiului AC'A'B'. Urmand in gand miscarea lui M cand d se roteste in jurul lui A, intuitia intareste presupunerea noastra, ea devenind plauzibila dar nu sigura. Este necesara o demonstratie care se face in doua etape.

a)         

Fig. 2.3

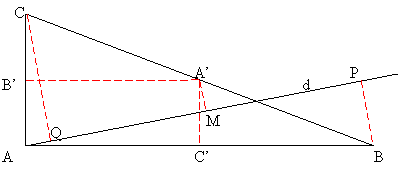Demonstram mai intai ca . Va trebui sa aratam ca . Paralela prin A' la BP si (CQ) intersecteaza pe d in mijlocul lui [PQ] (teorema paralelelor echidistante), deci in M. Cum , avem si deci . Rezulta ca M este situat pe arcul capabil de fata de [AA'], asadar (Fig.2.3).

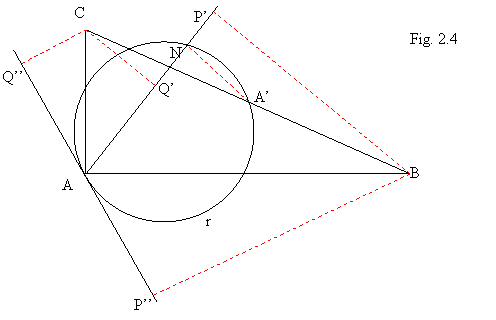
b)          Aratam ca orice punct apartine locului geometric. Daca , unim A cu N si proiectam B, C pe AN in P', Q' (Fig.2.4.). Unghiul fiind inscris intr-un semicerc este drept; rezulta ca BP', A'N, CQ' sunt paralele echidistante si N este mijlocul lui [P'Q']. Asadar, N apartine locului geometric. Daca N = A, se duce perpendiculara prin A pe AA' si se proiecteaza pe ea B si C in P", Q". Din nou se observa ca A este mijlocul segmentului [P"Q"], deci si in acest caz N apartine locului geometric.

Teorema 6: Locul geometric al punctelor care au aceeasi putere fata de doua cercuri neconcentrice este o dreapta perpendiculara pe linia centrelor, numita axa radicala a celor doua cercuri.

Demonstratie: Fie cele doua cercuri si , . Trebuie sa aflam locul geometric al punctelor M pentru care . Daca , atunci se poate nota si conditia se scrie . Deci trebuie gasit locul geometric al punctelor pentru care diferenta patratelor distantelor la doua puncte fixe este constanta. Se foloseste teorema lui Pitagora generalizata si se ajunge la faptul ca diferenta este constanta.

Teorema 7: Fiind date trei cercuri cu centrele necoliniare, axele lor radicale, luate doua cate doua, sunt concurente intr-un punct ce se numeste centrul radical al celor trei cercuri.

Demonstratie: Fie , , cele trei cercuri, iar axele radicale ale primelor, respectiv ultimelor doua cercuri. Srim ca si . Daca am avea d║, ar rezulta ca , ceea ce nu e posibil, fiind coliniare. Rezulta ca d si se taie intr-un punct P. deoarece P se gaseste pe d are aceeasi putere fata de si : cum P se gaseste si pe va avea aceeasi putere fata de cele trei cercuri. In particular P va avea aceeasi putere fata de si , adica va apartine celei de-a treia axe radicale.

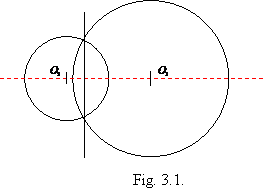
Constructia axei radicale. Daca doua cercuri au un punct comun, axa lor radicala trece prin acest punct (caci are puterea zero fata de ambele cercuri). Asadar:

In cazul cercurilor secante, axa radicala este secanta comuna (Fig.3.1). Daca cele doua cercuri sunt tangente, axa radicala este tangenta comuna (fiind perpendiculara pe linia centrelor) (Fig.3.2).

In cazul a doua cercuri fara puncte comune axa radicala se construieste in felul urmator: se traseaza un cerc ajutator care sa fie secant cu cele doua cercuri (Fig.3.3). ducem axele radicale ale perechilor de cercuri si le intersectam in P. perpendiculara din P pe dreapta ce uneste cele doua centre ale cercurilor initiale este axa radical.

			Fig. 3.2.

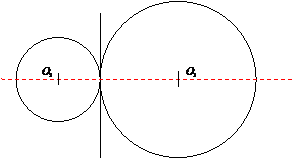
		Fig. 3.3.

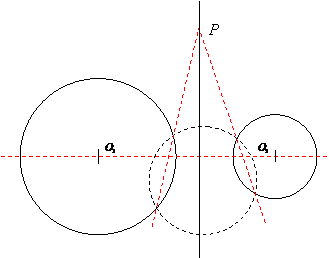
Teorema 8: Locul geometric al punctelor ale caror distante la doua puncte fixe sunt intr-un raport constant este un cerc (Cercul lui Apollonius).

Demonstratie: Fie A,B puncte fixe si k>1; atunci orice punct M al locului geometric este situat in semiplanul (dB, unde d este mediatoarea lui [AB]. Daca sunt intersectiile lui AB cu bisectoarea interioara si cea exterioara a lui , atunci, in conformitatea cu teorema bisectoarei unui unghi, , deci, punctele fixe apartin locului geometric. Pe de alta parte , deci M se afla pe un cerc P de diametru .

Recirpoc, orice punct apartine locului geometric. Intr-adevar, notand avem deci >1. Din ceea ce-am aratat mai sus rezulta ca N se afla pe un cerc de diamteru , unde . Daca >k punctele sunt mai aproape de B decat respectiv , deci , in contradictie cu . Daca k>, atunci si iarasi am ajuns la contradictie. Asadar singurul caz probabil este k= si deci N apartine locului geometric.

Daca k<1, se schimba rolul lui A si B si se obtine nu cerc in semiplanul (dA

In cazul k = 1, locul geometric este mediatoarea d