O1. Sa se rezolve sistemul:
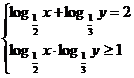
Rezolvare:
Conditii de existenta: x,y![]() R*+
R*+
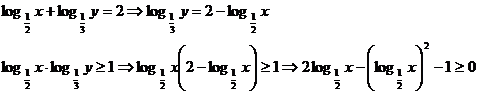
Ecuatia atasata: 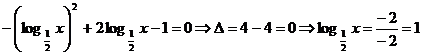
|
|
1 |
|
|
- - - - - - - 0 - - - - - - |
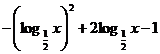
![]()
![]()
![]()
![]()
Deci ![]()
![]()
![]()
O2 Sa se gaseasca valorile lui x astfel incat:
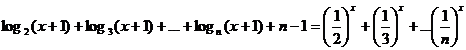
Raspuns:
Se observa ca x=0 este solutie
![]() =
=![]()
Se considera ![]() si
si
![]()
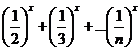
|
x= este
solutie unica a ecuatiei |
f(x) este strict crescatoare pe R
g(x) este strict descrescatoare pe R
O3 Fie a![]() R. Sa se rezolve
in R ecuatia:
R. Sa se rezolve
in R ecuatia: ![]()
Rezolvare:
![]()
O4 Sa se rezolve sistemul:
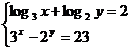
Rezolvare:
Conditii de existenta: x,y![]() R*+
R*+
Observam ca ![]() este solutie a
sistemului
este solutie a
sistemului
Verificare:
![]()
Cazul 1 x![]() (0;3)
(0;3)
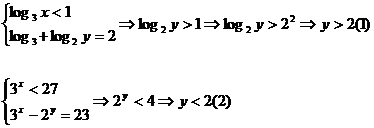
Din
relatiile (1) si (2)→contradictie→nu exista
solutii pentru x![]() (0;3) (3)
(0;3) (3)
Cazul 2 x![]() (3;+∞)
(3;+∞)
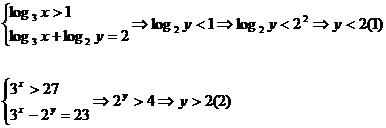
Din
relatiile (1) si (2)→contradictie→nu exista
solutii pentru x![]() (3;+∞) (4)
(3;+∞) (4)
Din relatiile (3)
si (4)→ecuatia
are solutie unica ![]()
O5 Sa se rezolve ecuatia:
4x+9x+25x=6x+10x+15x
Raspuns:
Observam ca x=0 verifica ecuatia.
Verificare: 1+1+1=1+1+1→3=3 (A)
Solutia 1:
Notam 2x=a
3x=b
5x=c
ecuatia 4x+9x+25x=6x+10x+15x se poate scrie a2+b2+c2=ab+ac+bc
a2+b2≥2ab
a2+c2≥2bc
b2+c2≥2ac +
![]() 2(a2+b2+c2)
≥2(ab+bc+ac)→ a2+b2+c2
≥ab+bc+ac
2(a2+b2+c2)
≥2(ab+bc+ac)→ a2+b2+c2
≥ab+bc+ac
Egalitatea are loc daca a=b=c → 3x=2x=5x→x=0
Solutia 2
4x+9x-6x =+10x+15x-25x ⁄ :10x
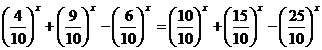
Definim urmatoarele functii:
|
|
Solutia unica este x=0
f(x)=
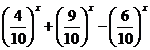 este strict
descrescatoare pe R
este strict
descrescatoare pe R
g(x)= 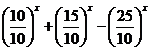 este strict
crescatoare pe R
este strict
crescatoare pe R
O6 Sa se rezolve ecuatia:
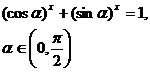
Rezolvare:
Observam ca x=2 este solutie a ecuatiei.
Verificare: ![]()
Definim urmatoarele functii:
|
|
f(x)=![]() ,
, ![]() →f(x) este strict descrescatoare pe R
→f(x) este strict descrescatoare pe R
g(x)=(sin ![]() )x,
)x, ![]() →g(x) este strict crescatoare pe R
→g(x) este strict crescatoare pe R
f(x)+g(x)=![]() este strict descrescatoare pe R
este strict descrescatoare pe R
Deci x=2 este solutie unica.
O7 Sa se rezolve ecuatia:
![]()
Rezolvare:
Observam ca x=5 este solutie a ecuatiei.
Verificare: 30=1→1=1 (A)
Definim functiile:
f:R→R,
f(x)=![]() este strict crescatoare pe R
este strict crescatoare pe R
g:R→R, g(x)= ![]() este strict descrescatoare pe R
este strict descrescatoare pe R
f(x)=![]()
x1<x2→x1-5<x2-5→![]() f(x1)<f(x2)→functia este
strict crescatoare
f(x1)<f(x2)→functia este
strict crescatoare
g(x)= ![]()
x1<x2 x1-4<x2-4→![]() g(x1)>g(x2)→functia este
strict descrescatoare
g(x1)>g(x2)→functia este
strict descrescatoare
Deci x=5 este solutie unica.
N1 Sa se rezolve inecuatiile:
a)
![]()
Rezolvare:
Conditii de existenta: x2+2x>0 x(x +2)=0
|
x |
-2 0 |
|
x(x-2) |
+ + +0- - - - - - 0+ + + + |
Ecuatia
atasata: x(x+2)=0 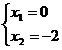
Deci x![]() (-∞;-2)
(-∞;-2)![]() (0;+ ∞).
(0;+ ∞).
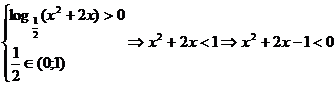
Ecuatia
atasata: x2+2x-1=0 ![]() =4+4=8.
=4+4=8.
|
x |
-1- |
|
x2+2x-1 |
+ 0 - - - - - - - 0 + + + |
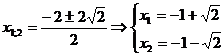
Deci
x![]() (-1-
(-1-![]() ;-1+
;-1+![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
Deci x![]() (-1-
(-1-![]() ;-2).
;-2).
c) ![]()
Rezolvare:
Conditii de existenta:
![]()
caz 1 x>1 ![]()
Ecuatia atasata: ![]()
![]() =4-4∙4∙5<0 inecuatia nu are solutii
=4-4∙4∙5<0 inecuatia nu are solutii
caz 2 x![]() (0;1)
(0;1) ![]()
Deci inecuatia nu are solutii.
A1 Sa se arate ca expresia 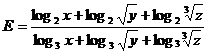 este independenta
de valorile strict mai mari ca 1 ale variabilelor x,y,z.
este independenta
de valorile strict mai mari ca 1 ale variabilelor x,y,z.
Rezolvare:
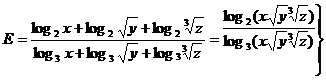
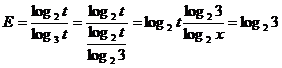
Notam ![]()
E este independenta de valorile x,y,z>1.