
I)Definitie:
Se conidera progresia aritmetica de ratie si si . Succesiunea se numeste progresie biaritmetica de ratii si .Din definitia de mai sus rezulta termenii progresiei biaritmetice de ratii si si relatiile prin care sunt dedusi:
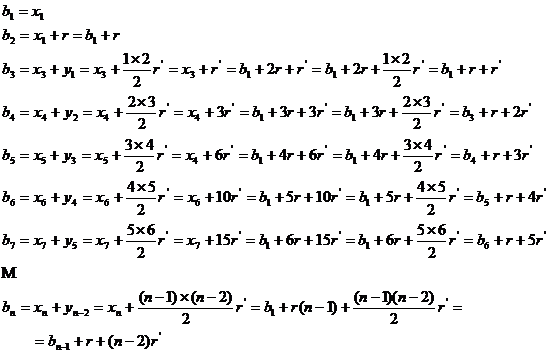
II) Termenul general al unei progresii biaritmetica
Din cele deduse mai sus rezulta ca termenul general al progresiei mentionate este:
![]()
![]()
III) Suma termenilor unei progresii biaritmetice
Fie
![]() o
progresie biaritmetica cu ratiile
o
progresie biaritmetica cu ratiile ![]() ri
ri ![]()
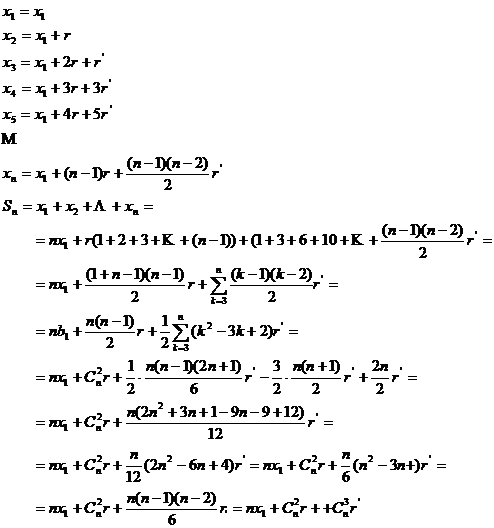
IV)Aplicatii
1).Sumele ![]() ,
,![]() , ale primilor
, ale primilor ![]() termeni ai unei
progresii aritmetice cu
termeni ai unei
progresii aritmetice cu ![]() termeni, formeaza o
progresie biaritmetica.
termeni, formeaza o
progresie biaritmetica.
Fie ![]() cu ratria
cu ratria ![]() ,
, ![]() si
si ![]()
![]()
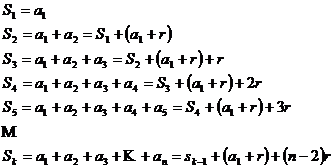
daca ![]() si
si ![]()
![]()
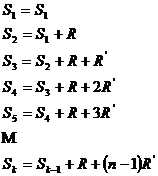
![]()
![]() cu
cu ![]() si
si ![]() ratiile progresiei
biaritmetice
ratiile progresiei
biaritmetice
EXEMPLU:
Fie ![]() cu termenul
general
cu termenul
general ![]() si ratia
si ratia ![]()
![]()
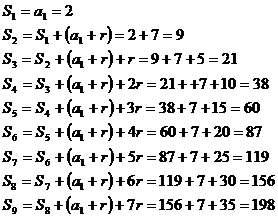
![]()
![]() unde
unde ![]() si
si ![]()
2. Patratele termenilor unei progresii aritmetice formeaza o progresie biaritmetica
Fie
![]() cu ratia
cu ratia ![]() si
si ![]()
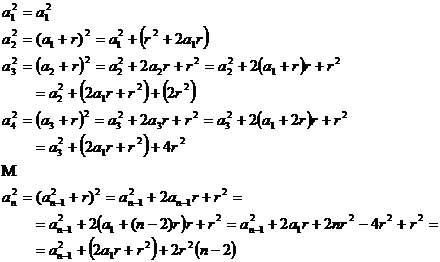
daca ![]() si
si ![]()
![]()
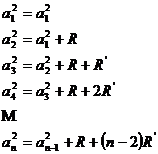
![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
EXEMPLU:
Fie ![]() o progresie aritmetica
cu ratia
o progresie aritmetica
cu ratia ![]() si cu
si cu ![]()
![]()
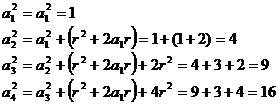
![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
3.Produsele termenilor de acelasi rang a doua progresii aritmetice cu acelasi numar de termeni formeaza progresie biaritmetica.
Fie ![]() de ratie
de ratie ![]() si
si ![]() de ratie
de ratie ![]()
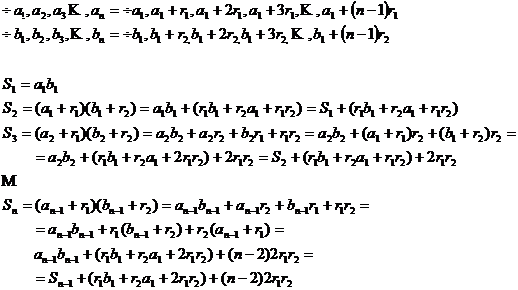
daca ![]()
![]() si
si ![]()
![]()
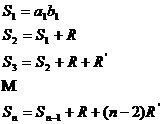
![]()
![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
EXEMPLU:
Fie ![]() de ratie
de ratie ![]() si
si![]() ;
;
![]() de ratie
de ratie ![]() si
si ![]()
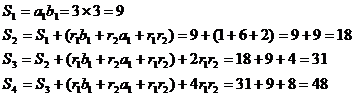
![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
4.Sumele termenilor de acelasi rang a doua progresii biaritmetice cu acelasi numar de termeni formeaza o progresie biaritmetica
Fie ![]() cu ratiile
cu ratiile ![]() si
si ![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
![]()
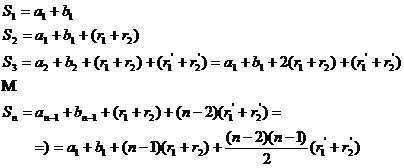
daca ![]() si
si ![]()
![]()
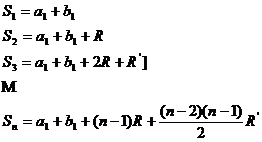
![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
5.Diferentele termenilor de acelasi rang a doua progresii biaritmetice cu acelasi numar de termeni formeaza o progresie biaritmetica.
Fie ![]() cu ratiile
cu ratiile ![]() si
si ![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
![]()
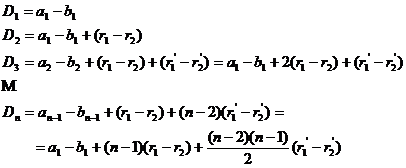
daca ![]() si
si ![]()
![]()
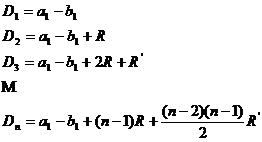
![]()
![]() cu ratiile
cu ratiile ![]() si
si ![]()
6.Daca
![]() este o progreseie biaritmetica , atunci
este o progreseie biaritmetica , atunci ![]() ,
, ![]() sunt termenii unei progresii aritmetice
sunt termenii unei progresii aritmetice
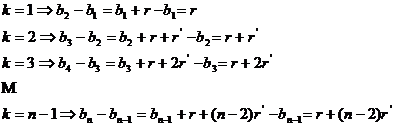
![]()
daca
![]()
![]()
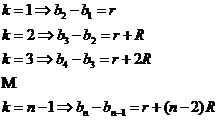
![]() cu ratia
cu ratia ![]()
I. DEFINITIE
II. TERMENUL GENERAL AL UNEI PROGRESII BIARITMETICE
III.SUMA TERMENILOR UNEI PROGRESII BIARITMETICE
IV.APLICATII
1.Sumele termenilor unei progresii aritmetice formeaza o progresie biaritmetica
2.Patratelel termenilor unei progresii aritmetice formeaza o progresie biaritmetica
3.Produsele termenilor de acelasi rang a doua progresii aritmetice cu acelasi numar de termeni
formeaza o progresie biaritmetica
4.Sumele termenilor de acelasi rang a doua progresii biaritmetice cu acelasi numar de termeni
formeaza o progresie biaritmetica
5. Diferentele termenilor de acelasi rang a doua progresii biaritmetice cu acelasi numar de
termeni
formeaza o progresie biaritmetica
6. Fie o progresie biaritmetica , atunci diferentele intre termenii consecutivi formeaza o progresie
aritmetica
BIBLIOGRAFIE
Articolul
"Progresii biaritmetice" de Traian Mada
-