Referat Matematica - Integrarea diferentialelor binome.Substitutile lui Cebisev



Calculul primitivelor de forma:
![]() unde
unde
![]() si
si ![]() .
.
Daca![]() sau
sau ![]() sau
sau![]()
![]() , atunci calculul primitivelor date se reduce la calculul
primitivei dintr-o functie rationala .
, atunci calculul primitivelor date se reduce la calculul
primitivei dintr-o functie rationala .
Intr-adevar , cu substitutia ![]() , avem
, avem ![]() , deci
, deci
![]() .
.
Cazul 1.
![]()
Sa punem ![]() unde
unde ![]() .Atunci substitutia
.Atunci substitutia ![]()
ne da ![]() ,deci
,deci
![]()
unde ![]() este functie rationala
deoarece
este functie rationala
deoarece ![]() .
.
Cazul 2.
![]()
Sa
punem ![]() , unde
, unde ![]() .Atunci substitutia
.Atunci substitutia ![]() ,ne da
,ne da ![]() ,deci
,deci
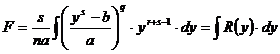
unde ![]() este functie rationala
deoarece
este functie rationala
deoarece ![]() .
.
Cazul 3.
![]()
Evident
avem ![]()
Sa
punem ![]() , unde
, unde ![]() . Atunci substitutia
. Atunci substitutia ![]() , ne da
, ne da 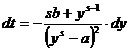 ,deci
,deci
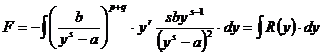
unde ![]() este functie rationala
deoarece
este functie rationala
deoarece ![]() .
.
Concluzie.
Prin urmare substitutile urmatoare :
![]() , daca
, daca ![]() , unde
, unde ![]() ;
;
![]() , daca
, daca ![]() , unde
, unde ![]() ;
;
![]() , daca
, daca ![]() , unde
, unde ![]() ,
,
reduc calculul
primitivei ![]() la calculul primitivei
dintr-o functie rationala .
la calculul primitivei
dintr-o functie rationala .
Observatie.
Cebisev
a aratat ca daca ![]() ,
,![]() si
si ![]() ,atunci primitiva data nu se poate reduce la primitiva
dintr-o functie rationala . Calculul primitivei nu poate fi facut atunci prin
mijloace elementare .
,atunci primitiva data nu se poate reduce la primitiva
dintr-o functie rationala . Calculul primitivei nu poate fi facut atunci prin
mijloace elementare .
Exemplul 1.
Sa se
calculeze primitiva 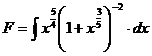 .
.
Avem ![]() , deci suntem in cazul 1.
, deci suntem in cazul 1.
Cum ![]() facem substitutia
facem substitutia
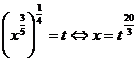 , deci
, deci ![]() si deci
si deci
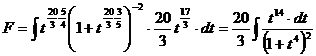
Exemplul 2.
Sa se calculeze primitiva 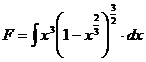
Avem ![]() si deci suntem in cazul 2.
si deci suntem in cazul 2.
Facem
substitutia 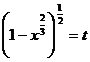 .Atunci
.Atunci ![]() , de unde obtinem :
, de unde obtinem :
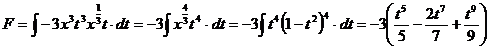
Exemplul 3.
Sa se calculeze primitiva 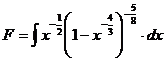
Avem ![]() ,
,![]() si
si ![]() ,deci
,deci ![]() si deci suntem in cazul 3. Facem substitutia
si deci suntem in cazul 3. Facem substitutia
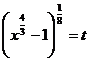 . Atunci
. Atunci ![]() , de unde obtinem :
, de unde obtinem :
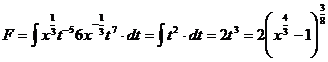
Exemplul 4.
Sa se calculeze primitiva ![]()
Avem functia
F=![]()
unde ![]()
![]()
Facem substitutia
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() si
obtinem :
si
obtinem :
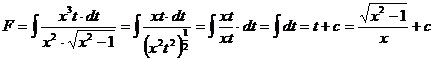
Exemplul 5.
Sa se calculeze primitiva ![]()
Avem ![]()
![]()
![]()
![]()
Facem
substitutia ![]()
![]()
![]()
![]()
![]()
![]() si
obtinem
si
obtinem
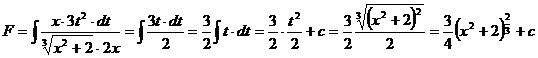
Exemplul 6.
Se se
calculeze primitiva 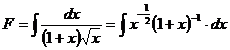
Avem ![]() , deci suntem in cazul 1.
, deci suntem in cazul 1.
Consideram
![]() , unde
, unde ![]()
![]()
![]() si
obtinem
si
obtinem
![]()