LODOVICO FERRARI si infrangerea ecuatiei de gradul IV

LODOVICO  FERRARI si infrangerea ecuatiei de gradul IV

Rezolvarea ecuatiei complete de gradul IV are loc relativ cam in aceeasi perioada cu aceea a ecuatiei de gradul III.

Conform scrierilor istorice,Cardano infiaza practic pe un elev al sau ,pe nume Lodovico Ferrari din Bologna ,talent ,matematic de mare forta.

Ferrari(1522-1565), a fost, in limbaj modern, asistentul lui Cardano.L-a insotit pe acesta in calatoriile sale stiintifice, l-a ajutat in redactarea monumentalei ,,Ars Magna" in care de fapt Cardano a si inclus metoda lui Ferrari de rezolvare a ecuatiei de gradul IV.

Ferrari a ajuns la solutia generala a ecuatiei de gradul IV tot in urma unei intreceri publice.

Conform cu Pietro Cossali(1748-1815), care a scris prin 1797 o istorie a algebrei, Giovanni Colla a propus lui Tartaglia o problema ce conduce la urmatorul sistem de ecuatii:

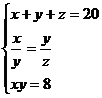
Prin eliminarea lui y si z, Tartaglia obtine ecuatia de gradul IV

Venind in contact cu disputa intre Colla si Tartaglia ,Cardano il atrage pe Ferrari in rezolvarea problemei. Acesta o rezolva in timp record, Cardano avand timpul necesar sa includa metoda in celebra ,,Ars Magna" (1545).

Practic, Ferrari a considerat o ecuatie de tipul:

p, q, n R

pe care, dupa o serie de artificii convenabile, o aduce la o asa-numita rezolventa de gradul III:

Sa consideram acum ecuatia de gradul IV sub forma uzuala:

x⁴ +px² +qx+r=0

Pentru orice real, are loc identitatea:

Il vom determina pe astfel incat sa aiba loc relatia:

(adica discriminantul trinomului din paranteza dreapta sa fie nul).

Ecuatia respectiva este de gradul III (rezolventa 1), deci odata determinat se poate scrie:

Asadar ecuatia de gradul IV se reduce la

sau adica la doua ecuatii simple de grad II .

Consideram polinomul general de grad IV  P(x)=x⁴ +ax³ +bx² +cx+d si dorim sa-l transformam astfel ca acesta sa poata fi scris ca diferenta a doua patrate perfecte:

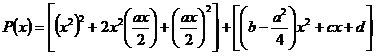
sau

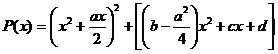
Introducem o necunoscuta auxiliara z in felul urmator :

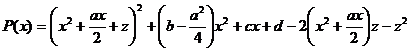
sau inca:

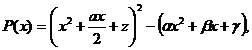
unde evident:

Bineinteles, polinomul este un patrat perfect, daca adica:

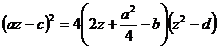
care nu este altceva decat rezolventa in cazul general.

Facem o observatie interesanta: daca z₀ este o radacina rationala a rezolvantei de mai inainte si expresiile:

sunt numere rationale, atunci polinomul P(x)= x⁴ +ax³ +bx² +cx+d este reductibil in campul numerelor rationale.

EXEMPLU: fie polinomul P(x)=6x⁴ -7x³ +x² -2.

Consideram polinomul inrudit :

si alcatuim rezolvarea acestuia:

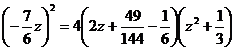
sau, prin substitutia 2z=u, obtinem rezolventa 180u³ -18u² +144u+25=0

Aceasta ecuatie are radacina rationala deci

Calculam pe rand expresiile:

Polinomul nostru se poate scrie in final ,

deci este reductibil.