Legi de conservare intr-o problema fara constrangeri referat

Legi de conservare intr-o problema fara constrangeri

Lasand deoparte constrangerea (2), vom relua problema de maximizare a integralei:

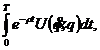
Aceasta problema poate fi privita ca un caz particular           

Pe baza acestui fapt, teoremele din sectiunea precedenta                              

.

Teorema 1 Pentru Lagrangianul , fie si ce satisfac ecuatiile:

,

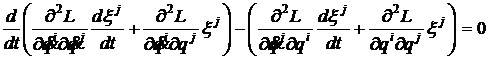pe o cale optimala pentru problema de maximizare a (1). Atunci cantitatea conservata W este data de:

.

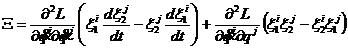Teorema 2 Pentru Lagrangianul (3) , fie ce satisface ecuatiile (7) pe o cale optimala pentru problema de maximizare a(1). Atunci cantitatea conservata W este data de:

.

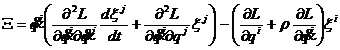Teorema 3 In Lagrangianul (3) , fie functia omogena de grad r in raport cu si . Atunci exista urmatoarea cantitate conservata pentru problama de maximizare a (1):

.

Pentru Lagrangianul de forma (3) , vom defini un Hamiltonian modificat (H fiind Hamiltonianul uzual):

,

unde r este gradul de omogenitate al lui U. Atunci cantitatea conservata (15) este scrisa , unde , care va fi redusa la o cantitate conservata ma tarziu.

Teorema 4 In Lagrngianul (3) , fie functia omogena de grad r in raport cu si .Atunci exista urmatoarele doua cantitati conservate pentru problema de maximizare a(1):

,

.

Noi legi de conservare in modelele de crestere economica

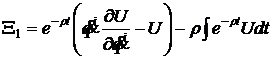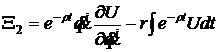Teoremele stabilite in sectiunea precedenta pot fi aplicate efectiv pentru derivarea unor noi legi de conservare in cateva modele de crestere economica.

i.            O generalizare a modelului de crestere de tipul von Neumann.

Prima aplicatie este data de n mijloace fixe si n mijloace de formare a capitalului fix . Deci in teorema 1, datorita teoremei 4, si sunt privite respectiv ca o functie de utilitate omogena de grad r si o functie de transformare omogena de gradul intai, in raport cu si , si r este rata de scont constanta.

In aceasta situatie, cantitatea conservata (15) se transforma imediat in:

In particular,pentru (=const.), cantitatea se reduce la:

Aceasta cantitate conservata nu poate fi separata in doua cantitati conservate independente prntru integrarea functiei.

In cazul , presupunem ca U este derivata totala in raport cu timpul a functiei omogena de gradul intai in raport cu , . Atunci U este omogena de gradul intai in raport cu , . Deci vom avea:

.

Prin urmare, cantitatile conservate (19) si (20) cu gradul de omogenitate conduc respectiv la:

,         ,

care sunt, in cazul , chiar cele ale lui Samuelson.

Pe de alta parte, dupa cum am vazut mai inainte, este o solutie ce satisface (6) si (7) pe un drum optim. Aici solutia se reduce la . Si, tinand seama de ecuatiile (5) cu si :

,

vom obtine imediat o alta solutie . Ambele cantitati conservate sau pot fi obtinute deci prin inlocuirea lui in (10) sau si in (8), respectiv.