METODA INDUCTIEI MATEMATICE
COMPLETE. ANALIZA COMBINATORIE. BINOMUL LUI NEWTON. SUME.
1. METODA INDUCTIEI MATEMATICE COMPLETE
Este o metoda de rationament prin care stabilim ca:
O proprietate P(n) care depinde de un numar natural n este verificata pentru orice numar natural n k atunci sunt satisfacute simultan conditiile:
a) Proprietatea P(n) este adevarata pentru n=k; kIN
b) (P(k), k n) T P(n+1), ( ) n k, adica presupunem P(k) adevarata pentru orice k n rezulta p(n+1) adevarata, pentru orice n k.
2. PERMUTARI
Fie E= o multime finita cu n elemente. Se numeste permutare a multimii E orice functie bijectiva f : E E.
![]()
Notam permutarea in felul
urmator
Notam numarul de permutari Pn: Pn= n!=1.2.3.n
conditie de existenta: nIN
conventie: 0!=1 ; 1!=1
Pn=n(n-1)!=n(n-1)(n-2)!
3. ARANJAMENTE
Notam cu Ank
Sistemele ordonate cu k elemente, care se pot forma cu elementele unei multimi cu n elemente (n k), se numesc aranjamente de n elemente luate cate k.
Ank=n!/(n-k)!=n(n-1)(n-2).(n-k+1)=(n-k+1)Ank-1
c.e. n k
conventie: n=k T Ann=Pn
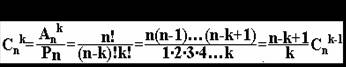
4. COMBINARI Cnk
conventie Cn0=Cnn=1 c.e. n k
Formule pentru combinari complementare: Cnk=Cnn-k
Cnk=Cn-1k+Cn-1k-1
5. BINOMUL LUI NEWTON
Daca a, bIR, nIN, atunci:
(a+b)n=Cn0an+Cn1an-1b+Cn2an-2b2+.+Cnkan-kbk+.+Cnn-1abn-1+Cnnbn
![]()
sau
Tk+1=termen general
k=se numeste rangul termenului al dezvoltarii
(a-b)n= Cn0an-Cn1an-1b+Cn2an-2b2-.+(-1)n-kCnkan-kbk+.+(-1)n-1Cnn-1abn-1+(-1)nCnnbn
![]()
sau
Obs 1) in dezvoltarea (a+b)n, dupa formula lui Newton, sunt n+1 termeni.
2) Cn0, Cn1, Cn2,.,Cnn se numesc coeficienti binomiali
3) Sa se faca distinctie intre coeficientul unui termen al dezvoltarii si coeficientul binomial al aceluiasi termen.

4) Pentru a determina rangul celui mai mare termen folosim relatia:
5) In dezvoltarea (a+b)n si (a-b)n, daca a=b atunci:
Cn0+Cn1+Cn2+.+Cnn=2n
Cn0+Cn2+Cn4+.=Cn1+Cn3+Cn5+.=2n-1
6) Identitatile utile:
a) Cnk=Cn-1k-1+Cn-2k-1+.+Ck-1k-1
b) Cn+kk=Cn0Cmk+Cn1Cmk-1+.+CnkCm0
7) Suma puterilor asemenea ale primelor n numere naturale
Folosim dezvoltarea (a+1)2=a2+2a+1 pentru demonstratie unde a=1,2,.n.
![]()
Folosim dezvoltarea (a+1)3=a3+3a2+3a+1,
pentru demonstratie, unde a=1,2,.n.
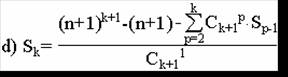
Folosim dezvoltarea (a+1)4=a4+4a3+6a2+4a+1,
pentru demonstratie, unde a=1,2,.n
![]()
Caz particular
6. PROGRESII ARITMETICE SI GEOMETRICE
![]()
Teorema : Fie numerele an-1, an, an+1 in progresie aritmetica. Atunci:
2an=an-1+an+1
Def Fie numerele a1, a2, a3,.,an in progresie aritmetica, daca an=a1+(n-1)r sau an=an-1+1, unde: an= ultimul termen
a1=primul termen
an-1=penultimul termen
n=numarul de termeni
r=ratia progresiei aritmetice
![]()
Obs Pentru verificare r=a2-a1=a3-a2=a4-a3=.=an-an-1
![]()
Teorema Fie numerele bn-1, bn, bn+1
in progresie geometrica. Atunci
bn2=bn-1.bn+1
Def Fie numerele b1, b2,.bn in progresie geometrica, daca bn=b1.qn sau bn=bn-1.q unde: bn=ultimul termen
b1=primul termen bn-1=penultimul termen n=numarul de termeni q=ratia progresiei geometrice
![]()
Obs pentru verificare q=a2/a1=a3/a2=.=an/an-1