Graficele functiilor trigonometrice
In trasarea graficelor functiiolr trigonometrice se urmaresc mai multe etape:
I
a) gasirea domeniul maxim de definitie a functiei
b) gasirea intersectiei graficului cu axa Ox (f(x)=0)
![]()
c) gasirea
intersectiei graficului cu axa Oy (se calculeaza f(0) )
a) se studiaza paritatea sau imparitatea functiei
b) se studiaza periodicitatea functiei
c) se studiaza continuitatea functiei
d) se studiaza semnul functiei pe domeniul de definitie
a) se cauta asimptota orizontala
b) se cauta asimptota oblica
c) se cauta asimptota verticala in punctele de acumulare unde functia nu este definita
a) se calculeaza derivata I
b) se gasesc radacinile derivatei I si valoarea functiei in aceste radacini
c) se gaseste semnul derivatei I
a) se calculeaza derivata II
b) se gasesc radacinile derivatei II si valoarea functiei in aceste radacini
c) se gaseste semnul derivatei II
VII
a) se traseaza graficul functiei
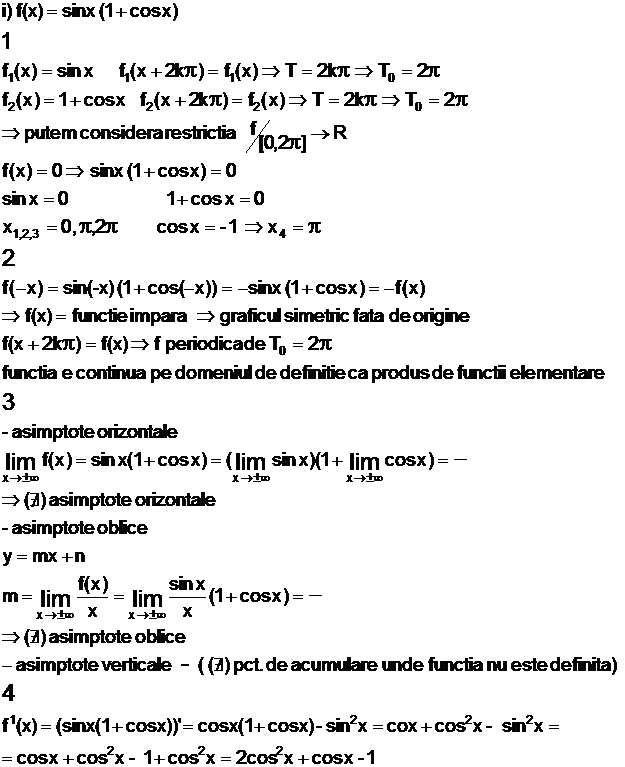
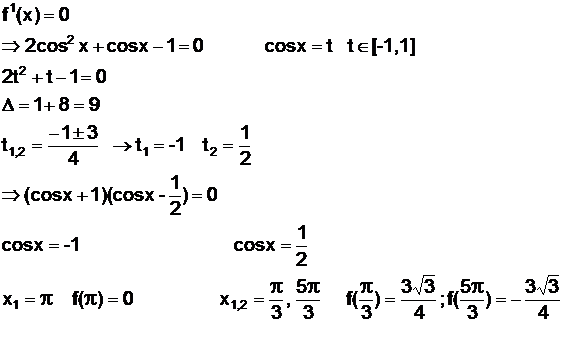
x |
p 3 p 5p/3 |
|
cosx+1 |
+ + + 0 + + + + + |
|
cosx+ |
+ 0 - - - - - - - 0 + + + |
|
|
+ + 0 - - - - 0 - - - - 0 + + + |
|
x |
p- arccos p p+ arccos 2p |
|
-sin x |
- - - - - - - - 0 + + + + + 0 |
|
4cosx+1 |
+ + + 0 - - - - - - - 0 + + + + + |
|
f''(x) |
0 - - - - 0 + + + + 0 - - - - 0 + + + + + 0 |
VI
|
x |
p 3 p- arccos p p+ arccos 5p 3 2p |
|
f'(x) |
+ + + 0 - - - - - - - 0 - - - - - - 0 + + + |
|
f''(x) |
- - - - - 0 + + 0 - - - 0 + + + + + + 0 |
|
f(x) |
|
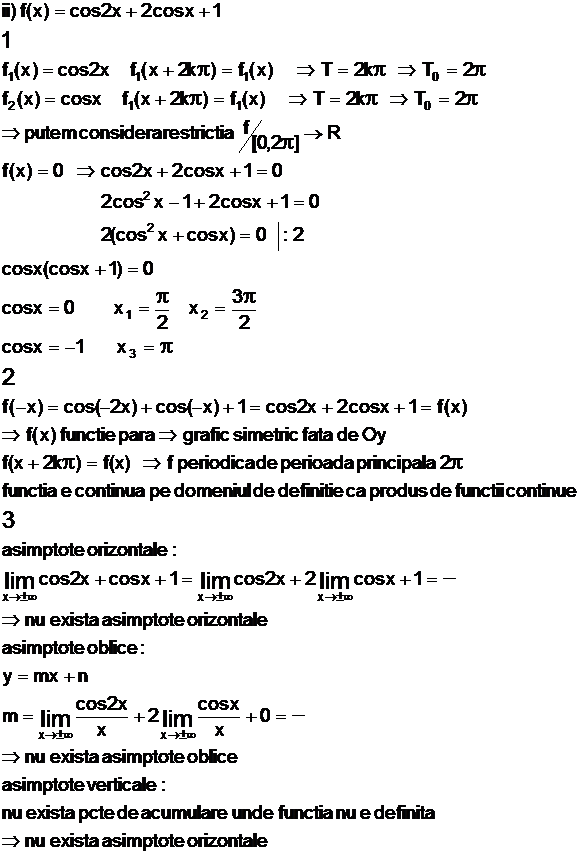
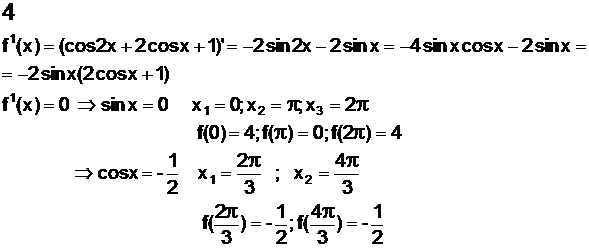
|
x |
p p p 2p |
|
-2sinx |
0- - - - - 0 + + + + + + |
|
2cosx+1 |
+ + + 0 - - - - 0 + + + + + |
|
|
- - - - 0 + + + 0 - - - 0 + + + + + + + |
x |
x1 p/3 x3 p x4 p x2 p |
|
f1(x) |
- - - - - - - 0 + + + + 0 - - - - - - 0 + + + + + 0 |
|
f2(x) |
- - - - -0 + + + + + 0 - - - - -0 + + + + + + 0 - - - - |
|
f(x) |
4 1.88 -0.5 -0.26 0 -0.26 -0.5 1.88 4 |

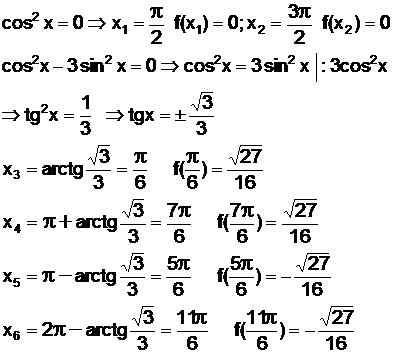
|
x |
p 5p 7p 3p 11p 2p |
|
cos²x-3sin²x |
+ + + + 0 - - - 0 + + 0 - - - - - - - 0 + + + + + |
|
cos²x |
+ + + 0 + + + + + + + + 0 + + + + + + |
|
|
+ + 0 - - - -0 + + +0 - - - 0 - - - 0 + + + + + |
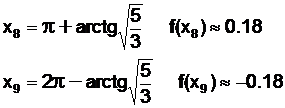
|
x |
p p 3p 2p |
|
sinx |
+ + + + + + + +0 - - - - - - - - - 0 |
|
cosx |
+ + + + 0 - - - - - - - 0 + + + + |
|
-sinxcosx |
0 - - - - 0 + + + 0 - - - - 0 + + + 0 |
|
x |
0 p/2 2.22 p 4.05 3p/2 5.37 2p |
|
-sinxcosx |
0 - - - 0 + + + 0 - - - - 0 + + + 0 |
|
10cos²-sin²x |
+ + 0 - - - - 0 + + + + 0 - - - - - 0 + + + |
|
f2(x) |
- - 0 + +0 - 0 + + 0 - - 0 + + + 0 - - 0 + + 0 |
|
x |
0 p/6 0.91 p/2 2.22 5p/6 p 7p/6 4.05 3p/2 5.37 11p/6 2p |
|
f1(x) |
+ 0 - - - 0 - - - - 0 + + + 0 - - - - 0 - - - - 0 + + |
|
f2(x) |
- - - 0 + +0 - - 0 + + + + 0 - - - - - 0 + + 0 - - 0 + + + + 0 |
|
f(x) |
0 0.32 0.18 0 -0.18 -0.32 0 0.32 0.18 0 -0.18 -0.32 0 |
Se obseva ca graficul functiei pe intervalul [0, p] este identic cu cel pe intervalul (p p], in consecinta vom reprezenta functia doar pe intervalul [0, p
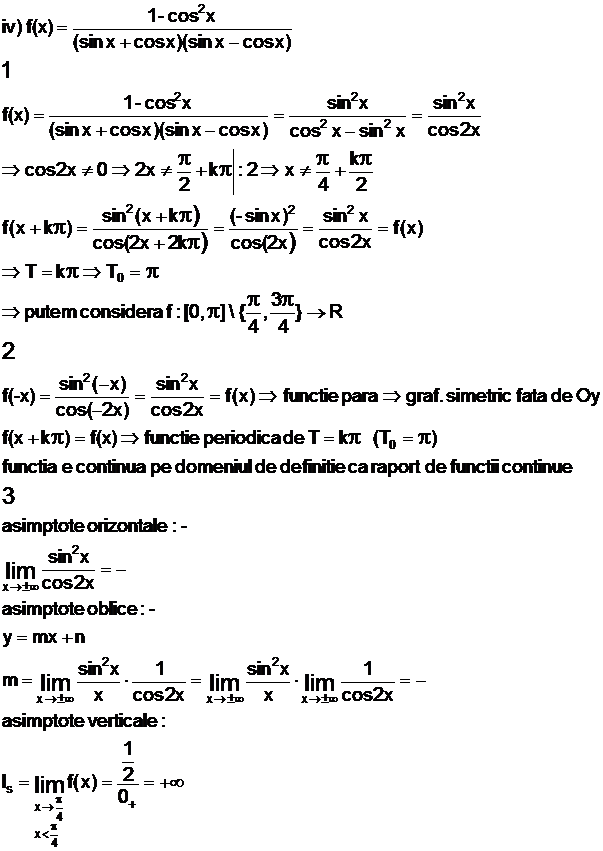
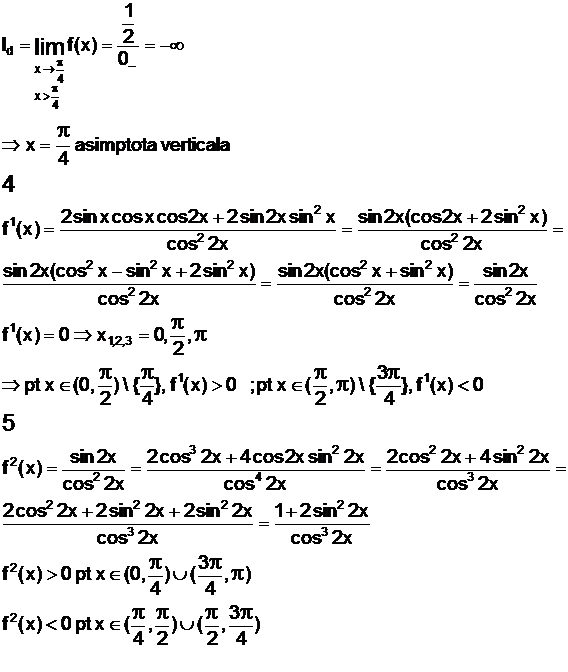
|
x |
p p p p |
|
f1(x) |
+ + + I + + + + 0 - - - - - I - - - - - - 0 |
|
f2(x) |
+ + + + I - - - - - - - - - - - - - I + + + + + + |
|
f(x) |
+ I- -1 - I+ 0 |
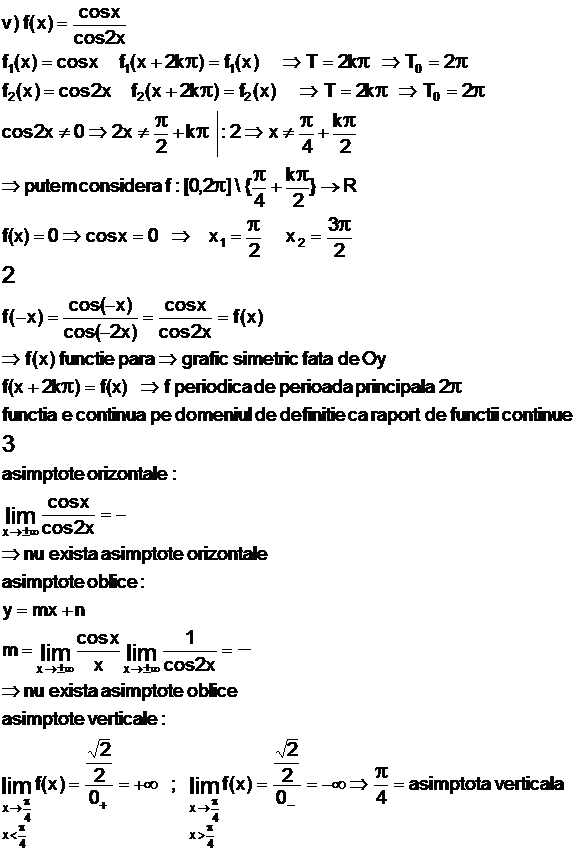
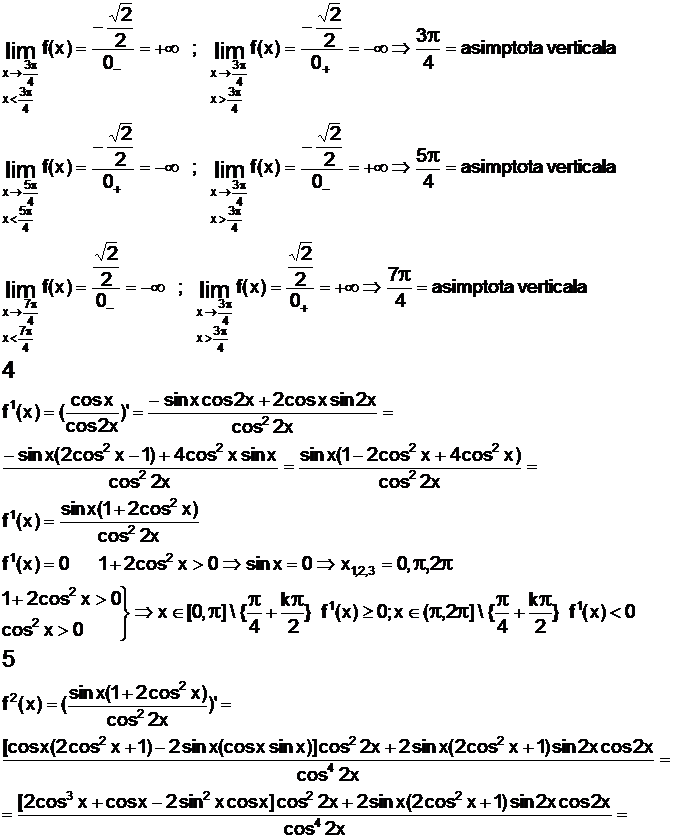
|
|
0 p p 3p 5p 3p 7p 2p |
|
cosx |
+ + + 0 - - - - - - - - - 0 + + + + + + |
|
cos 2x |
+ + 0 - - - - - - - 0 + + + 0 - - - - - - - - - 0 + + + |
|
r |
+ + +I - - - - 0 + + + I - - - - - I + + + +0 - - - - - I + + + |
|
x |
p p 3p/4 p 5p 3p 7p/4 2p |
|
f1(x) |
+ + I + + + + + + I + + 0 - - - I - - - - - - - - - I - - - - 0 |
|
f2(x) |
+ + + I - - - - 0 + + + I - - - - - - -I + + + +0 - - - - - I + + + |
|
f(x) |
1 + I- 0 + I- -1 - I+ 0 - I+ |
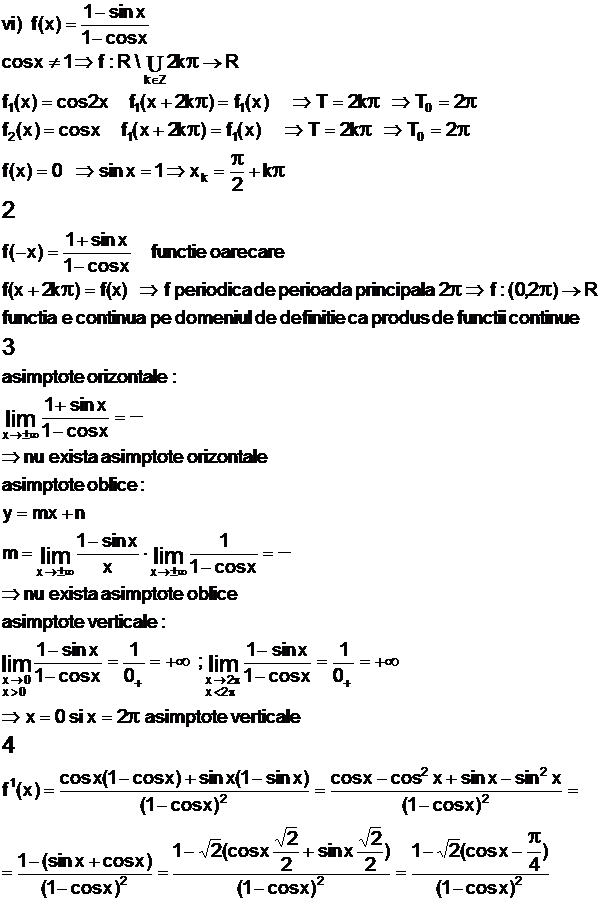
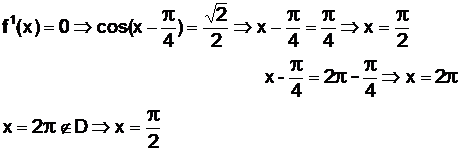
x |
0 p p 3p/4 p 5p 3p 7p 2p |
|
f1(x) |
- - - - - 0 + + + + + + + + + + + + + + + + + + |
|
f(x) |
I+ 1 0 0.17 ½ 1 2 5.82 + I |